空间站广场

论文

Notebooks

比赛

课程

Apps

镜像市场

我的主页

我的Notebooks

我的知识库

我的足迹

我的工作空间

任务

节点

镜像

文件

数据集

项目

数据库

公开

PyTorch Tutorial | 5.Automatic Differentiation with torch.autogrd

python

PyTorch

pythonPyTorch

Weipeng Xu

更新于 2024-12-16

推荐镜像 :Basic Image:ubuntu:22.04-py3.10-pytorch2.0

推荐机型 :c2_m4_cpu

Tensors, Functions and Computational graph

Computing Gradients

Disable Gradient Tracking

Tensors, Functions and Computational graph

代码

文本

[23]

import torch

x = torch.ones(5)

y = torch.zeros(3)

'''

Equavalient to

w = torch.rand(5,3)

w.requires_grad_(True)

'''

w = torch.randn(5, 3, requires_grad=True)

b = torch.randn(3, requires_grad=True)

print(f"w: {w}")

print(f"b: {b}")

z = torch.matmul(x,w) + b

print(f"z: {z}")

loss = torch.nn.functional.binary_cross_entropy_with_logits(z,y)

print(f"loss: {loss}")

w: tensor([[-0.6828,  0.3332, -1.9763],
        [-0.1963,  0.8592,  0.4308],
        [ 0.0557, -2.1140, -0.9972],
        [ 1.3912, -0.5062,  1.6108],
        [ 0.5042, -0.6462, -0.2771]], requires_grad=True)
b: tensor([-0.4456, -1.4925,  0.9890], requires_grad=True)
z: tensor([ 0.6264, -3.5665, -0.2200], grad_fn=<AddBackward0>)
loss: 0.5572206974029541

代码

文本

The above codes define the following computational graph. The tensor w and b are the parameters to be optimized, so we set requires_grad=True.

代码

文本

alt

代码

文本

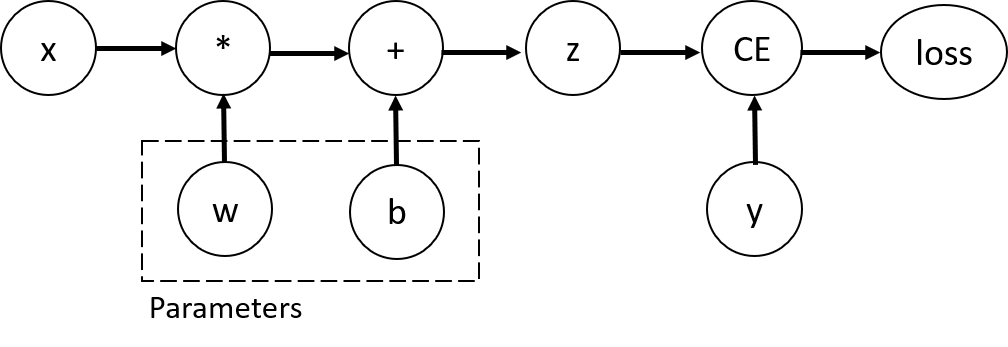
The tensors use Function object to constrcut the computational graph. This object knows how to compute the function in the forward and how to compute the derivatives in the backward propagation. The latter is stored in the grad_fn of a tensor. Also see Function.

代码

文本

[24]

print(f"Gradient function for x: {x.grad_fn}")

print(f"Gradient function for y: {y.grad_fn}")

print(f"Gradient function for w: {w.grad_fn}")

print(f"Gradient function for b: {b.grad_fn}")

print(f"Gradient function for z: {z.grad_fn}")

print(f"Gradient function for loss: {loss.grad_fn}")

Gradient function for x: None
Gradient function for y: None
Gradient function for w: None
Gradient function for b: None
Gradient function for z: <AddBackward0 object at 0x7f18b82b8820>
Gradient function for loss: <BinaryCrossEntropyWithLogitsBackward0 object at 0x7f18b855f250>

代码

文本

Computing Gradients

代码

文本

To compute the derivatives

$\frac{\partial loss}{\partial w}, \frac{\partial loss}{\partial b}$

we can use

代码

文本

[35]

'''

'backward' can only be called once on a given graph for performance reasons

If several calls are required, set the property 'retain_graph = True'

'''

loss.backward(retain_graph=True)

print(w.grad)

print(b.grad)

tensor([[2.3895, 0.1008, 1.6324],
        [2.3895, 0.1008, 1.6324],
        [2.3895, 0.1008, 1.6324],
        [2.3895, 0.1008, 1.6324],
        [2.3895, 0.1008, 1.6324]])
tensor([2.3895, 0.1008, 1.6324])

代码

文本

The gradient information will

代码

文本

[40]

'''

Gradient is only available for leaf nodes in the computational graph with `requires_grad=True`.

'''

print(x.grad)

print(y.grad)

print(z.grad)

None
None
None
/tmp/ipykernel_61/3184559473.py:7: UserWarning: The .grad attribute of a Tensor that is not a leaf Tensor is being accessed. Its .grad attribute won't be populated during autograd.backward(). If you indeed want the .grad field to be populated for a non-leaf Tensor, use .retain_grad() on the non-leaf Tensor. If you access the non-leaf Tensor by mistake, make sure you access the leaf Tensor instead. See github.com/pytorch/pytorch/pull/30531 for more informations. (Triggered internally at aten/src/ATen/core/TensorBody.h:489.)
  print(z.grad)

代码

文本

Disable Gradient Tracking

代码

文本

Somtimes we don't want to do the gradient tracking, for example

mark some paramters in NN as forzen paramters
speed up computations when you only need to do the forward pass

At thsi time, we can stop gradient trackling by

代码

文本

[45]

z = torch.matmul(x, w) + b

print(z.requires_grad)

# using torch.no_grad()

with torch.no_grad():

z = torch.matmul(x, w) + b

print(z.requires_grad)

z = torch.matmul(x, w) + b

print(z.requires_grad)

# using detach()

z_det = z.detach()

print(z_det.requires_grad)

True
False
True
False

代码

文本

More on Computational Graphs

代码

文本

Conceptually, autograd keeps a record of data (tensors) and all executed operations (along with the resulting new tensors) in a directed acyclic graph (DAG) consisting of Function objects. In this DAG, leaves are the input tensors, roots are the output tensors. By tracing this graph from roots to leaves, you can automatically compute the gradients using the chain rule.

In the forward pass, autograd does two things simultaneously:

run the requested operation to compute a resulting tensor
maintain the operation's gradient function in the DAG

The backward pass begins after the .backward() being called on the DAG root. Then autograd

computes the gradients from each .grad_fn
accumulates them in the respective tensor's .grad attribute
using the chain rule, propagates all the way to the leaf tensors

The DAGs in PyTorch are dynamic, which means that after each backward call, autograd will starts populating a new graph.

代码

文本

Tensor Gradients and Jacobian Products

代码

文本

When the loss function not a scalar but an arbitary tensor, PyTorch allows us to compute the Jacobian product but not the actual gradient.

With the input $x = ⟨ x_{1}, \dots, x_{n} ⟩$ and the output $y = ⟨ y_{1}, \dots, y_{m} ⟩$ we have the following Jacobian marix $J = \frac{\partial y _{1}}{\partial x _{1}} ⋮ \frac{\partial y _{m}}{\partial x _{1}} \dots ⋱ \dots \frac{\partial y _{1}}{\partial x _{n}} ⋮ \frac{\partial y _{m}}{\partial x _{n}}$ Then we can calculated the Jacobian Product $v^{T} \cdot J$ for a given vector $v = (v_{1}, \dots, v_{m})$ by

代码

文本

[50]

inp = torch.eye(4, 5, requires_grad=True)

# t() means the tranpose

out = (inp+1).pow(2).t()

out.backward(torch.ones_like(out), retain_graph=True)

print(f"First call\n{inp.grad}")

# the gradient of each leaf node will be accumulated after the second call

out.backward(torch.ones_like(out), retain_graph=True)

print(f"Second call\n{inp.grad}")

# to compute the proper gradients, do

inp.grad.zero_()

out.backward(torch.ones_like(out))

print(f"Call after zeroing gradients\n{inp.grad}")

# optimizer will help us to do the zero out operation

First call
tensor([[4., 2., 2., 2., 2.],
        [2., 4., 2., 2., 2.],
        [2., 2., 4., 2., 2.],
        [2., 2., 2., 4., 2.]])
Second call
tensor([[8., 4., 4., 4., 4.],
        [4., 8., 4., 4., 4.],
        [4., 4., 8., 4., 4.],
        [4., 4., 4., 8., 4.]])
Call after zeroing gradients
tensor([[4., 2., 2., 2., 2.],
        [2., 4., 2., 2., 2.],
        [2., 2., 4., 2., 2.],
        [2., 2., 2., 4., 2.]])

代码

文本

Tensors, Functions and Computational graph

Computing Gradients

Disable Gradient Tracking

More on Computational Graphs

Tensor Gradients and Jacobian Products

Further Reading