UMAP降维算法——强大的机器学习降维算法

空间站广场

论文

Notebooks

比赛

课程

Apps

我的主页

我的Notebooks

我的论文库

我的足迹

我的工作空间

任务

节点

文件

数据集

镜像

项目

数据库

公开

UMAP降维算法——强大的机器学习降维算法

Machine Learning

中文

AI4S

python

Machine Learning中文AI4Spython

Cui Yaning

发布于 2023-11-05

推荐镜像 :Third-party software:ai4s-cup-0.1

推荐机型 :c2_m4_cpu

UMAP降维算法

1.拓扑数据分析

2.寻找低维表示

3.Python中使用UMAP

4.总结

UMAP降维算法

UMPA（Uniform Manifold Approximation and Projection）是一种基于流形学习技术和拓扑数据分析思想的降维算法。它为流形学习和降维提供了一个非常通用的框架，同时也能提供具体的实现方法。本文将讨论该算法在实践中是如何工作的。虽然有更深层次的数学基础，但为了普通读者的可读性，这些基础只是参考和链接。如果您想了解数学描述，请参阅 UMAP 论文。

UMAP的名称涵盖了其主要原理和设计思想：

Uniform（均匀）：UMAP假设数据样本均匀分布在流形上，但实际情况往往是不均匀的。这引入了距离可变性的概念，即空间在不同位置会扭曲，根据数据的密度而变化。UMAP的设计目标是尽可能减小这种均匀性假设的影响，以便更好地保留数据的全局结构

Manifold（流形）：流形是一种数学概念，用于描述在每个点附近局部类似于欧几里得空间的拓扑空间。UMAP旨在在低维空间中保留数据流形的结构，以便更好地捕捉数据的内在关系。

Projection（投影）：UMAP通过将高维数据投影到低维空间来实现降维。这意味着它将高维数据点映射到一个较低维度的空间，以便更好地可视化和分析数据。

Approximation（近似）：UMAP算法使用有限的数据样本来近似表示数据流形，而不是考虑整个流形。这意味着它基于样本数据来构建流形的估计，以在低维空间中准确地再现数据的结构。

即假设可用数据样本均匀（Uniform）分布在流形（Manifold）上，可以从这些有限数据样本中近似（Approximation）并投影（Projection）到低维空间。

代码

文本

1.拓扑数据分析

单纯形（Simplex）是用简单组合成分构建拓扑空间的一种方法。，我们就可以把处理拓扑空间连续几何的复杂性简化为相对简单的组合和计数任务。这种处理几何和拓扑学的方法将是我们进行拓扑数据分析以及维度缩减的基础。

0-simplex是一个点，1-simplex是线段（在两个0-simplex之间），2-simplex是三角形（以三个1-simplex作为面），而 3-simplex是四面体（以四个2-simplex作为面）。这样简单结构可以轻松泛化到任意尺寸。

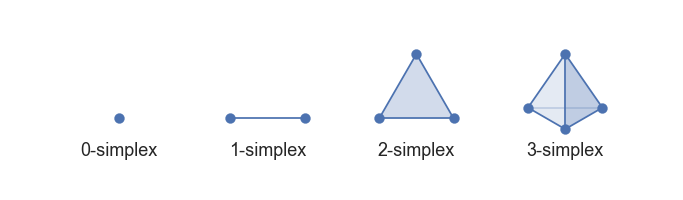
alt image.png

对于任意长度的数据，我们可以构造k-simplex，其有k+1个面构成。所以，我们始终可以通过几何形状实现对这个抽象集描述，方法是构造相应的几何单纯形。

代码

文本

以一个噪声正弦波的测试数据集为例

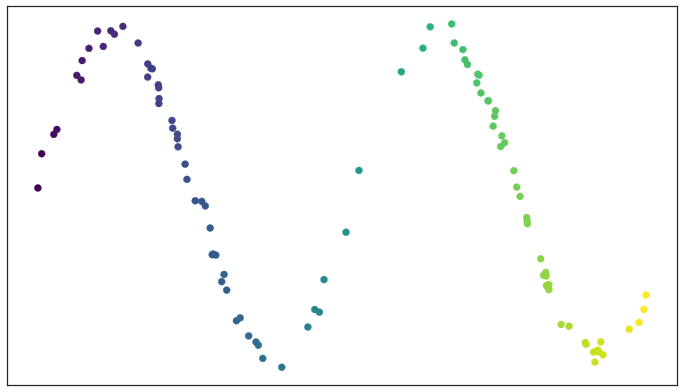
alt image.png

UMAP 首先使用 Nearest-Neighbor-Descent 算法找到最近的邻居。我们可以通过调整 UMAP 的 n_neighbors 超参数来指定我们想要使用多少个近邻点。

试验 n_neighbors 的数量很重要，因为它控制 UMAP 如何平衡数据中的局部和全局结构。它通过在尝试学习流形结构时限制局部邻域的大小来实现。

本质上，一个小的n_neighbors 值意味着我们需要一个非常局部的解释，准确地捕捉结构的细节。而较大的 n_neighbors 值意味着我们的估计将基于更大的区域，因此在整个流形中更广泛地准确。

alt image.png

接下来，我们要确保试图学习的流形结构不会导致许多不连通点。所以需要使用另一个超参数local_connectivity(默认值= 1)来解决这个潜在的问题

当我们设置local_connectivity=1 时，我们告诉高维空间中的每一个点都与另一个点相关联。

Local_connectivity(默认值为1)：100%确定每个点至少连接到另一个点(连接数量的下限)。

n_neighbors(默认值为15)：一个点直接连接到第 16 个以上的邻居的可能性为 0%，因为它在构建图时落在 UMAP 使用的局部区域之外。

2 到 15 ：有一定程度的确定性（>0% 但 <100%）一个点连接到它的第 2 个到第 15 个邻居。

由于我们采用了不同距离的方法，因此从每个点的角度来看，我们不可避免地会遇到边缘权重不对齐的情况。例如，点 A→B 的边权重与 B→A 的边权重不同。

alt image.png

如果我们想将权重为 a 和 b 的两条不同的边合并在一起，那么我们应该有一个权重为 + − ⋅ 的单边。考虑这一点的方法是，权重实际上是边（1-simplex）存在的概率。组合权重就是至少存在一条边的概率。

最后，我们得到一个连接的邻域图

alt image.png

代码

文本

2.寻找低维表示

从高维空间学习近似流形后，UMAP 的下一步是将其投影（映射）到低维空间。

与第一步不同，我们不希望在低维空间表示中改变距离。相反，我们希望流形上的距离是相对于全局坐标系的标准欧几里得距离。

从可变距离到标准距离的转换的转换也会影响与最近邻居的距离。因此，我们必须传递另一个名为 min_dist（默认值=0.1）的超参数来定义嵌入点之间的最小距离。

本质上，我们可以控制点的最小分布，避免在低维嵌入中许多点相互重叠的情况。

指定最小距离后，该算法可以开始寻找较好的低维流形表示。 UMAP 通过最小化交叉熵（CE）来实现。

最终目标是在低维表示中找到边的最优权值。这些最优权值随着上述交叉熵函数的最小化而出现，这个过程是可以通过随机梯度下降法来进行优化的

现在UMAP的工作完成了，我们得到了一个数组，其中包含了指定的低维空间中每个数据点的坐标。

代码

文本

3.Python中使用UMAP

上面我们已经介绍UMAP的知识点，现在我们在Python中进行实践。

我们将在MNIST数据集(手写数字的集合)上应用UMAP，以说明我们如何成功地分离数字并在低维空间中显示它们。

代码

文本

[1]

#安装UMAP库

!pip install umap-learn -i https://pypi.tuna.tsinghua.edu.cn/simple

Looking in indexes: https://pypi.tuna.tsinghua.edu.cn/simple, https://pypi.ngc.nvidia.com
Requirement already satisfied: umap-learn in /opt/conda/lib/python3.8/site-packages (0.5.4)
Requirement already satisfied: numba>=0.51.2 in /opt/conda/lib/python3.8/site-packages (from umap-learn) (0.53.1)
Requirement already satisfied: scikit-learn>=0.22 in /opt/conda/lib/python3.8/site-packages (from umap-learn) (0.24.2)
Requirement already satisfied: numpy>=1.17 in /opt/conda/lib/python3.8/site-packages (from umap-learn) (1.22.4)
Requirement already satisfied: pynndescent>=0.5 in /opt/conda/lib/python3.8/site-packages (from umap-learn) (0.5.10)
Requirement already satisfied: scipy>=1.3.1 in /opt/conda/lib/python3.8/site-packages (from umap-learn) (1.6.3)
Requirement already satisfied: tqdm in /opt/conda/lib/python3.8/site-packages (from umap-learn) (4.64.0)
Requirement already satisfied: tbb>=2019.0 in /opt/conda/lib/python3.8/site-packages (from umap-learn) (2021.10.0)
Requirement already satisfied: llvmlite<0.37,>=0.36.0rc1 in /opt/conda/lib/python3.8/site-packages (from numba>=0.51.2->umap-learn) (0.36.0)
Requirement already satisfied: setuptools in /opt/conda/lib/python3.8/site-packages (from numba>=0.51.2->umap-learn) (59.5.0)
Requirement already satisfied: joblib>=0.11 in /opt/conda/lib/python3.8/site-packages (from pynndescent>=0.5->umap-learn) (1.1.0)
Requirement already satisfied: threadpoolctl>=2.0.0 in /opt/conda/lib/python3.8/site-packages (from scikit-learn>=0.22->umap-learn) (3.1.0)
WARNING: Running pip as the 'root' user can result in broken permissions and conflicting behaviour with the system package manager. It is recommended to use a virtual environment instead: https://pip.pypa.io/warnings/venv

代码

文本

[2]

# Data manipulation

import pandas as pd # for data manipulation

import numpy as np # for data manipulation

# Visualization

import plotly.express as px # for data visualization

import matplotlib.pyplot as plt # for showing handwritten digits

# Skleran

from sklearn.datasets import load_digits # for MNIST data

from sklearn.model_selection import train_test_split # for splitting data into train and test samples

# UMAP dimensionality reduction

from umap import UMAP

/opt/conda/lib/python3.8/site-packages/tqdm/auto.py:22: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html
  from .autonotebook import tqdm as notebook_tqdm

代码

文本

接下来，我们加载MNIST数据并显示前10个手写数字的图像。

代码

文本

[3]

# Load digits data

digits = load_digits()

# Load arrays containing digit data (64 pixels per image) and their true labels

X, y = load_digits(return_X_y=True)

# Some stats

print('Shape of digit images: ', digits.images.shape)

print('Shape of X (main data): ', X.shape)

print('Shape of y (true labels): ', y.shape)

# Display images of the first 10 digits

fig, axs = plt.subplots(2, 5, sharey=False, tight_layout=True, figsize=(12,6), facecolor='white')

n=0

plt.gray()

for i in range(0,2):

for j in range(0,5):

axs[i,j].matshow(digits.images[n])

axs[i,j].set(title=y[n])

n=n+1

plt.show()

代码

文本

现在，我们将之前加载到X中的MNIST数字数据。X(1797,64)的形状告诉我们我们有1797个数字，每个数字由64个维度组成。

我们将使用UMAP将维数从64降到3，并打印转换后的数组的形状。

代码

文本

[4]

# Configure UMAP hyperparameters

reducer = UMAP(n_neighbors=100, # default 15, The size of local neighborhood (in terms of number of neighboring sample points) used for manifold approximation.

n_components=3, # default 2, The dimension of the space to embed into.

metric='euclidean', # default 'euclidean', The metric to use to compute distances in high dimensional space.

n_epochs=1000, # default None, The number of training epochs to be used in optimizing the low dimensional embedding. Larger values result in more accurate embeddings.

learning_rate=1.0, # default 1.0, The initial learning rate for the embedding optimization.

init='spectral', # default 'spectral', How to initialize the low dimensional embedding. Options are: {'spectral', 'random', A numpy array of initial embedding positions}.

min_dist=0.1, # default 0.1, The effective minimum distance between embedded points.

spread=1.0, # default 1.0, The effective scale of embedded points. In combination with ``min_dist`` this determines how clustered/clumped the embedded points are.

low_memory=False, # default False, For some datasets the nearest neighbor computation can consume a lot of memory. If you find that UMAP is failing due to memory constraints consider setting this option to True.

set_op_mix_ratio=1.0, # default 1.0, The value of this parameter should be between 0.0 and 1.0; a value of 1.0 will use a pure fuzzy union, while 0.0 will use a pure fuzzy intersection.

local_connectivity=1, # default 1, The local connectivity required -- i.e. the number of nearest neighbors that should be assumed to be connected at a local level.

repulsion_strength=1.0, # default 1.0, Weighting applied to negative samples in low dimensional embedding optimization.

negative_sample_rate=5, # default 5, Increasing this value will result in greater repulsive force being applied, greater optimization cost, but slightly more accuracy.

transform_queue_size=4.0, # default 4.0, Larger values will result in slower performance but more accurate nearest neighbor evaluation.

a=None, # default None, More specific parameters controlling the embedding. If None these values are set automatically as determined by ``min_dist`` and ``spread``.

b=None, # default None, More specific parameters controlling the embedding. If None these values are set automatically as determined by ``min_dist`` and ``spread``.

random_state=42, # default: None, If int, random_state is the seed used by the random number generator;

metric_kwds=None, # default None) Arguments to pass on to the metric, such as the ``p`` value for Minkowski distance.

angular_rp_forest=False, # default False, Whether to use an angular random projection forest to initialise the approximate nearest neighbor search.

target_n_neighbors=-1, # default -1, The number of nearest neighbors to use to construct the target simplcial set. If set to -1 use the ``n_neighbors`` value.

#target_metric='categorical', # default 'categorical', The metric used to measure distance for a target array is using supervised dimension reduction. By default this is 'categorical' which will measure distance in terms of whether categories match or are different.

#target_metric_kwds=None, # dict, default None, Keyword argument to pass to the target metric when performing supervised dimension reduction. If None then no arguments are passed on.

#target_weight=0.5, # default 0.5, weighting factor between data topology and target topology.

transform_seed=42, # default 42, Random seed used for the stochastic aspects of the transform operation.

verbose=False, # default False, Controls verbosity of logging.

unique=False, # default False, Controls if the rows of your data should be uniqued before being embedded.

)

# Fit and transform the data

X_trans = reducer.fit_transform(X)

# Check the shape of the new data

print('Shape of X_trans: ', X_trans.shape)

/opt/conda/lib/python3.8/site-packages/umap/umap_.py:1943: UserWarning: n_jobs value -1 overridden to 1 by setting random_state. Use no seed for parallelism.
  warn(f"n_jobs value {self.n_jobs} overridden to 1 by setting random_state. Use no seed for parallelism.")
Shape of X_trans:  (1797, 3)

代码

文本

接下来，我们将创建一个用于绘制3D散点图的函数，我们可以多次重用该函数来显示UMAP降维的结果。

代码

文本

[5]

def chart(X, y):

#--------------------------------------------------------------------------#

# This section is not mandatory as its purpose is to sort the data by label

# Concatenate X and y arrays

arr_concat=np.concatenate((X, y.reshape(y.shape[0],1)), axis=1)

# Create a Pandas dataframe using the above array

df=pd.DataFrame(arr_concat, columns=['x', 'y', 'z', 'label'])

# Convert label data type from float to integer

df['label'] = df['label'].astype(int)

# Finally, sort the dataframe by label

df.sort_values(by='label', axis=0, ascending=True, inplace=True)

#--------------------------------------------------------------------------#

labels_ele = set(y)

fig = plt.figure(dpi=240)

ax = fig.add_subplot(projection='3d')

# Create a 3D graph

for i in labels_ele:

dfnew = df[df['label']==i]

ax.scatter(dfnew['x'], dfnew['y'], dfnew['z'],)

# Update marker size

fig.show()

代码

文本

[12]

#Another plot based on ploty

def chart_ploty(X, y):

#--------------------------------------------------------------------------#

# This section is not mandatory as its purpose is to sort the data by label

# so, we can maintain consistent colors for digits across multiple graphs

# Concatenate X and y arrays

arr_concat=np.concatenate((X, y.reshape(y.shape[0],1)), axis=1)

# Create a Pandas dataframe using the above array

df=pd.DataFrame(arr_concat, columns=['x', 'y', 'z', 'label'])

# Convert label data type from float to integer

df['label'] = df['label'].astype(int)

# Finally, sort the dataframe by label

df.sort_values(by='label', axis=0, ascending=True, inplace=True)

#--------------------------------------------------------------------------#

# Create a 3D graph

fig = px.scatter_3d(df, x='x', y='y', z='z', color=df['label'].astype(str), height=900, width=950)

# Update chart looks

fig.update_layout(title_text='UMAP',

showlegend=True,

legend=dict(orientation="h", yanchor="top", y=0, xanchor="center", x=0.5),

scene_camera=dict(up=dict(x=0, y=0, z=1),

center=dict(x=0, y=0, z=-0.1),

eye=dict(x=1.5, y=-1.4, z=0.5)),

margin=dict(l=0, r=0, b=0, t=0),

scene = dict(xaxis=dict(backgroundcolor='white',

color='black',

gridcolor='#f0f0f0',

title_font=dict(size=10),

tickfont=dict(size=10),

yaxis=dict(backgroundcolor='white',

color='black',

gridcolor='#f0f0f0',

title_font=dict(size=10),

tickfont=dict(size=10),

zaxis=dict(backgroundcolor='lightgrey',

color='black',

gridcolor='#f0f0f0',

title_font=dict(size=10),

tickfont=dict(size=10),

)))

# Update marker size

fig.update_traces(marker=dict(size=3, line=dict(color='black', width=0.1)))

fig.show()

代码

文本

[7]

chart(X_trans, y)

代码

文本

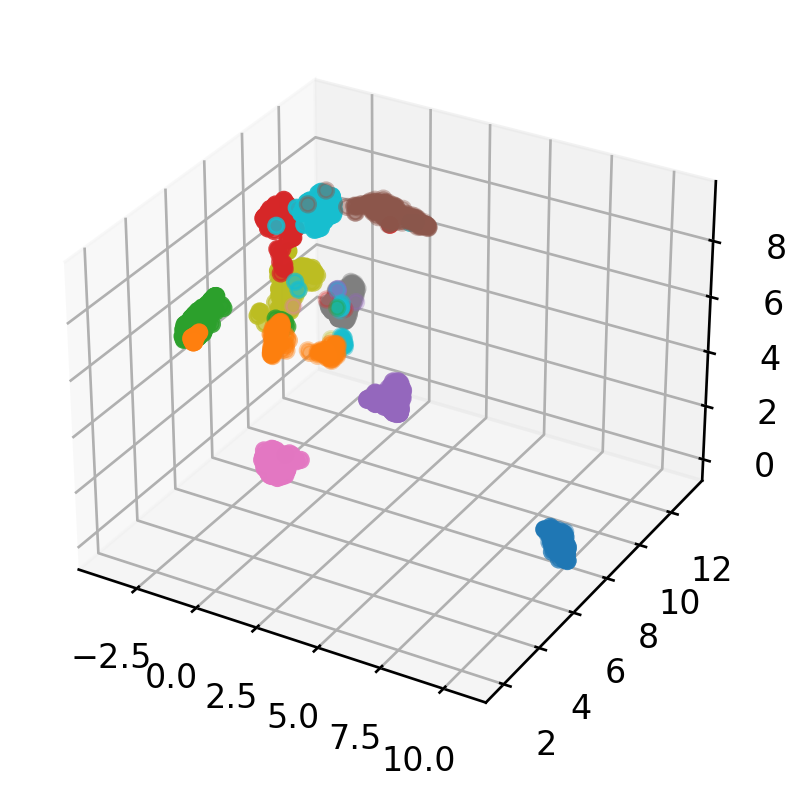
我们还可以以监督的方式使用UMAP来帮助减少数据的维数。

代码

文本

[8]

# Split data into training and testing

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, shuffle=False)

# Configure UMAP hyperparameters

reducer2 = UMAP(n_neighbors=100, n_components=3, n_epochs=1000,

min_dist=0.5, local_connectivity=2, random_state=42,

)

# Training on MNIST digits data - this time we also pass the true labels to a fit_transform method

X_train_res = reducer2.fit_transform(X_train, y_train)

# Apply on a test set

X_test_res = reducer2.transform(X_test)

# Print the shape of new arrays

print('Shape of X_train_res: ', X_train_res.shape)

print('Shape of X_test_res: ', X_test_res.shape)

/opt/conda/lib/python3.8/site-packages/umap/umap_.py:1943: UserWarning: n_jobs value -1 overridden to 1 by setting random_state. Use no seed for parallelism.
  warn(f"n_jobs value {self.n_jobs} overridden to 1 by setting random_state. Use no seed for parallelism.")
Shape of X_train_res:  (1347, 3)
Shape of X_test_res:  (450, 3)

代码

文本

[9]

chart(X_train_res, y_train)

代码

文本

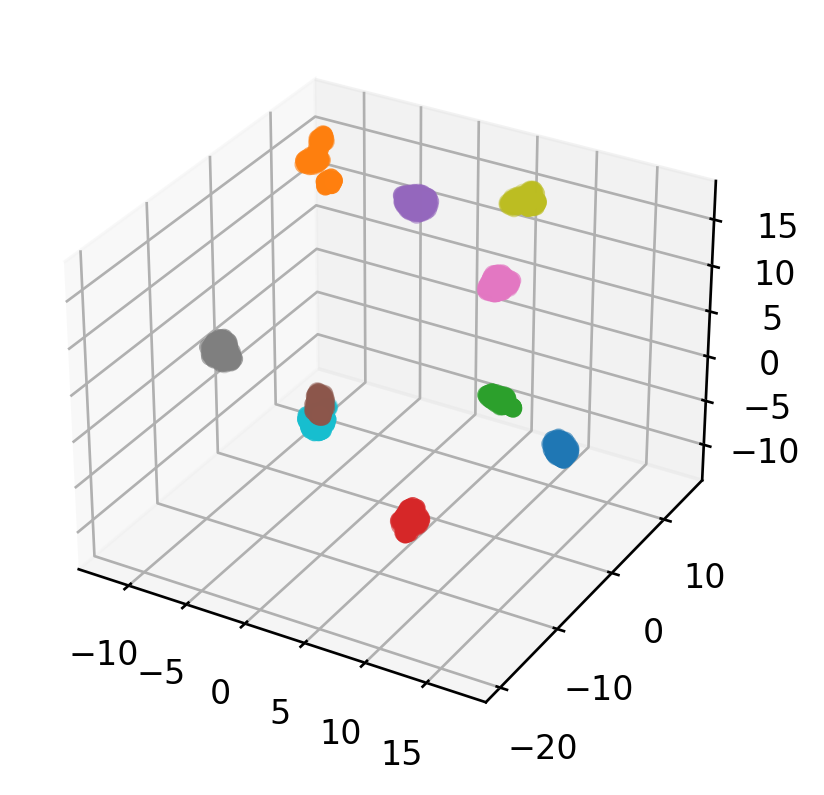
4.总结

感谢您阅读这篇长文，我希望它的每一部分都能让您更深入地了解这个伟大的算法是如何运行的。

一般来说，UMAP具有坚实的数学基础，它通常比t-SNE等类似的降维算法做得更好。

UMAP的秘诀在于保持低维空间中相对全局距离的同时推断局部和全局结构的能力。

代码

文本

Machine Learning

中文

AI4S

python

Machine Learning中文AI4Spython

点个赞吧

本文被以下合集收录

机器学习

zxh136978

更新于 2024-07-10

17 篇1 人关注