分子动力学算法介绍

引言

分子动力学（Molecular Dynamics, MD）是一种通过数值求解牛顿运动方程来模拟和研究分子系统随时间演化的方法。MD广泛应用于物理学、化学、生物学等领域，用于研究原子和分子的行为、相互作用及动力学特性。

势能面

势能面的概念

势能面（Potential Energy Surface, PES）是描述分子系统中势能随原子位置变化的多维函数。在一个多原子体系中，势能面是一个高维空间，表示所有可能的分子构型及其对应的势能。势能面对于理解化学反应路径、过渡态和稳定态等具有重要意义。

特殊点和最低点

在势能面上，有几个重要的点值得关注：

1. 局部最低点（Local Minima）：这些点对应于体系的局部最低势能状态，体系在这些位置是稳定的，可能对应于不同的分子构型或相态。
2. 全局最低点（Global Minimum）：这是势能面的最低点，表示体系的基态，体系在这个位置是最稳定的。
3. 鞍点（Saddle Points）：这些点对应于势能面的过渡态，体系在这些位置的势能是局部最高的，但沿某些方向则为最低。这些点对化学反应和相变等过程至关重要。

计算最低点的方法

找到势能面的最低点是分子动力学中的一个重要任务。常用的方法包括：

1. 梯度下降法（Gradient Descent）：通过沿着势能梯度的负方向不断迭代来找到最低点。适用于简单势能面的优化。
2. 共轭梯度法（Conjugate Gradient）：一种改进的梯度下降法，通过结合前几步的信息加速收敛，适用于大规模体系。
3. 牛顿-拉夫森法（Newton-Raphson）：利用势能的二阶导数（Hessian矩阵）来加速收敛，但计算复杂度较高，适用于势能面光滑的情况。

势能函数及其作用

势能函数的定义

在分子动力学模拟中，势能函数（Potential Energy Function）是描述分子体系中原子或分子间相互作用的数学函数。它决定了体系的势能面，并影响体系的动力学行为和稳定性。

常见的势能函数

1. Lennard-Jones 势：

   • 用途：描述非极性分子间的范德华力相互作用。
   • 公式：$U(r)=4ϵ\left[{\left(\frac{\sigma }{r}\right)}^{12}-{\left(\frac{\sigma }{r}\right)}^6\right]$
   • 参数：$ϵ$为深度势阱，$\sigma$为两原子间相互作用为零的距离。

2. 库仑势：

   • 用途：描述带电粒子间的静电相互作用。
   • 公式：$U(r)=\frac{k_e{q}_1{q}_2}{r}$
   • 参数：$k_e$为库仑常数，$q_1$和$q_2$为两粒子的电荷，$r$为两粒子间的距离。

3. 弹性势：

   • 用途：描述共价键的伸缩和角度弯曲。
   • 公式：
     • 键伸缩：$U(r)=\frac{1}{2}k(r-r_0{)}^2$
     • 角度弯曲：$U(\theta )=\frac{1}{2}k(\theta -{\theta }_0{)}^2$
   • 参数：$k$为力常数，$r_0$为平衡键长，${\theta }_0$为平衡角度。

势能函数的作用

势能函数在MD模拟中起着至关重要的作用，它决定了分子体系的稳定构型和动态行为。通过适当的势能函数，可以模拟不同类型的分子相互作用和化学反应路径。

运动积分算法

运动积分的概念

运动积分是指通过数值方法求解经典力学中的运动方程，以预测粒子在未来时刻的位置和速度。在MD模拟中，运动积分的目标是通过对牛顿运动方程的离散化，计算分子系统随时间的演化过程。

牛顿运动方程为：
$\mathbf{F}=m\mathbf{a}$
$\mathbf{a}=\frac{{\mathrm{d}}^2\mathbf{r}}{\mathrm{d}{t}^2}$
其中，$\mathbf{F}$是作用在粒子上的力，$m$是粒子的质量，$\mathbf{a}$是粒子的加速度，$\mathbf{r}$是粒子的位置。

运动积分在MD算法中的意义

计算运动积分的主要原因是为了模拟和预测分子系统在不同条件下的动态行为。这些行为包括：

1. 分子构型的变化：了解分子在不同温度、压力下的构型变化。
2. 化学反应过程：模拟化学反应的路径和过渡态。
3. 物理性质：计算体系的热力学性质和动力学性质，如扩散系数、粘度等。

常用的积分算法

1. Verlet算法：

   • 优点：算法简洁，数值稳定。
   • 公式：$r(t+\Delta t)=2r(t)-r(t-\Delta t)+a(t)\Delta t^2$
   • 适用场景：常用于简单的分子动力学模拟。

2. Velocity Verlet算法：

   • 优点：能够同时更新位置和速度，提高精度。
   • 公式：
     • $v(t+\frac{\Delta t}{2})=v(t)+\frac{1}{2}a(t)\Delta t$
     • $r(t+\Delta t)=r(t)+v(t+\frac{\Delta t}{2})\Delta t$
     • $v(t+\Delta t)=v(t+\frac{\Delta t}{2})+\frac{1}{2}a(t+\Delta t)\Delta t$
   • 适用场景：适用于需要同时考虑速度和位置更新的场景。

3. Beeman算法：

   • 优点：对速度更新进行了进一步优化，具有更高的精度。
   • 公式：
     • $r(t+\Delta t)=r(t)+v(t)\Delta t+\frac{2}{3}a(t)\Delta t^2-\frac{1}{6}a(t-\Delta t)\Delta t^2$
     • $v(t+\Delta t)=v(t)+\frac{1}{3}a(t+\Delta t)\Delta t+\frac{5}{6}a(t)\Delta t-\frac{1}{6}a(t-\Delta t)\Delta t$
   • 适用场景：适用于需要高精度速度更新的场景。

相空间概念及其在MD中的应用

相空间的概念

相空间（Phase Space）是一个抽象的多维空间，其中每一个维度对应于体系的一个自由度。在经典力学中，对于一个由 (N) 个粒子组成的体系，相空间的维数为 (6N)（每个粒子有3个位置坐标和3个动量坐标）。相空间的一个点表示体系在某一时刻的完全状态，即所有粒子的位置和动量。

相空间中的运动

在相空间中，体系的演化可以视为相空间中一点的轨迹。根据李维尔定理（Liouville's Theorem），在哈密顿系统中，相空间体积是守恒的，即随着时间的推移，相空间中一点的密度不变。这一性质在MD模拟中用于描述体系的统计力学性质。

相空间在MD中的应用

1. 系综的表示：不同的热力学系综可以通过相空间的不同区域来表示。例如，NVE系综对应于相空间中能量恒定的表面。
2. 态点的分布：通过统计相空间中的态点分布，可以计算体系的宏观热力学性质。
3. 时间相关函数：在相空间中，通过轨迹计算时间相关函数（如自相关函数）来研究体系的动力学性质。

系综的选择

在MD模拟中，不同的热力学系综用于描述不同条件下的体系。常见的系综包括：

NVE系综（微正则系综）

• 描述：粒子数（N）、体积（V）和能量（E）保持不变。
• 适用场景：适用于孤立体系的研究，不与外界交换能量。

NVT系综（正则系综）

• 描述：粒子数（N）、体积（V）和温度（T）保持不变。
• 实现方法：通过恒温器（如Berendsen恒温器、Nosé-Hoover恒温器）控制体系温度。
• 适用场景：适用于恒温条件下的体系研究，如生物分子模拟。

NVT 系综的实现

NVT系综中温度的控制通常通过速度重标（Velocity Rescaling）来实现。其基本思想是通过调整粒子的速度来达到目标温度。

from scipy.constants import Boltzmann
import numpy as np

def velocity_rescaling(velocities, target_temperature):
    current_temperature = np.sum(velocities**2) / (3 * len(velocities) * Boltzmann)
    scaling_factor = np.sqrt(target_temperature / current_temperature)
    return velocities * scaling_factor

NPT系综（等温等压系综）

• 描述：粒子数（N）、压强（P）和温度（T）保持不变。
• 实现方法：通过恒压器（如Berendsen恒压器、Parrinello-Rahman恒压器）控制体系压强。
• 适用场景：适用于恒压恒温条件下的体系研究，如相变模拟。

分子动力学模拟的基本步骤

初始化

1. 选择体系：确定模拟体系的类型，如气体、液体、固体或生物分子。选择合适的原子或分子模型和力场参数。
2. 定义初始条件：设置初始原子坐标和速度。初始坐标可以通过实验数据或其他模拟方法获得，初始速度通常通过最大熵分布生成，使体系达到期望的温度。

势能计算

计算体系中所有粒子间的相互作用力，这通常需要通过势能函数进行。势能函数决定了分子体系的相互作用和动态行为。

时间步长选择

选择适当的时间步长（通常在1-2飞秒），以确保数值积分的精度和模拟的稳定性。时间步长过大会导致积分不稳定，时间步长过小会增加计算量。

运动积分

通过数值方法求解牛顿运动方程，更新粒子的位置和速度。常用的运动积分算法包括Verlet算法、Velocity Verlet算法和Beeman算法。

系综控制

根据选择的系综，通过恒温器和恒压器控制体系的温度和压强，确保模拟符合热力学统计平衡态。例如，NVT系综使用恒温器控制温度，NPT系综使用恒温器和恒压器控制温度和压强。

数据采集

在模拟过程中定期采集体系的物理量（如能量、温度、压强、径向分布函数等），用于后续的分析和计算。数据采集的频率需要根据模拟的时间尺度和物理现象的变化速度来确定。

结果分析

通过对模拟数据的统计分析，计算体系的热力学和动力学性质，如自由能、扩散系数、粘度等。分析方法包括时间相关函数、自相关函数、径向分布函数等。

结果分析和应用

计算热力学性质

通过MD模拟，可以计算分子体系的热力学性质，如：

1. 能量：包括总能量、动能、势能和内部能。
2. 温度：通过粒子的动能计算体系的温度。
3. 压强：通过动量流密度计算体系的压强。

计算动力学性质

通过分析粒子的运动轨迹，可以计算体系的动力学性质，如：

1. 扩散系数：通过均方位移计算粒子的扩散系数，描述分子的扩散行为。
2. 粘度：通过自相关函数和动量流密度计算体系的粘度。
3. 自相关函数：用于分析粒子的运动相关性和振动模式。

模拟化学反应

通过MD模拟，可以研究化学反应的路径、过渡态和反应机理。常用的方法包括反应坐标扫描、自由能计算和反应路径优化。

应用领域

MD模拟在许多领域有广泛的应用：

1. 材料科学：研究材料的力学性质、热力学性质和相变行为。
2. 生物分子：模拟蛋白质、核酸和膜的结构与动力学，研究分子识别、配体结合和蛋白质折叠。
3. 化学反应：研究化学反应的动力学、过渡态和反应机理。

总结

分子动力学是一种强大的模拟工具，通过数值积分牛顿运动方程来模拟分子体系的动态行为。通过详细介绍势能面、运动积分算法、相空间概念和系综的选择，本文展示了MD模拟的基本原理和应用方法。分子动力学在材料科学、生物学和化学等领域具有广泛的应用前景，通过调整模拟参数和势能函数，可以深入研究不同条件下的分子行为，进一步理解物理化学现象和生物过程。

使用DPMD计算钪的熔点

钪的基本性质

钪（Scandium，元素符号：Sc）是化学元素周期表中的第21号元素，相对原子质量44.96，属于过渡金属。它呈银白色，密度约为2.985 g/cm³，熔点约为1541°C，沸点约为2830°C。钪在空气中较稳定，但在潮湿环境中容易氧化，常见的化合价为+3。

钪在地壳中的丰度较低，约为22 ppm，主要存在于钪钇矿、钪铝榴石等矿物中，通常作为其他稀土矿物的副产品进行提取。尽管钪在自然界中的含量不高，但其在工业中具有重要应用价值。钪常用于铝合金中以增加强度和减轻重量，尤其在航空航天领域广泛应用。此外，钪还用于制造高强度放电灯，如金属卤化物灯，并在核反应堆中用作中子吸收材料。

钪对生物体没有已知的生物学功能，也不是必需的元素，但其化合物具有一定的毒性。钪于1879年由瑞典化学家拉斯·弗雷德里克·尼尔森（Lars Fredrik Nilson）发现，并命名。总体而言，钪虽然在自然界中含量较少，但因其优良的物理和化学性质，在现代工业中具有不可忽视的重要性。

由Scandium-wikipedia介绍，钪单质晶体为hcp结构，晶格常数$a=330.89pm$，$c=526.80pm$。

输入文件

我们首先需要钪晶体的DP模型。科学智能广场提供了非常丰富的深势模型，我们找到Sc单质晶体的DP-PBE模型：Sc_model.pb文件。

该模型通过DP势分子动力学模拟和第一性原理计算系统地研究了钪的晶格常数、空位/间隙形成能、表面能和扩散系数，α-β相变温度、熔点等力学性能，以及弹性常数和广义层错能（GSFE）曲线。我们利用其原子模型和力场参数进行计算。

其次还需要输入命令文件Sc.in。

根据教程编写命令文件。

输入相对原子质量44.96，选取的深度势能文件为Sc_model.pb，计算时原子速度随机分布，在1200-1600温度内进行计算。设置时间步长为1fs，运行总步数为70000。

这里步长的设置，从计算精度的要求讲宜小不宜大。但是在相同的总时间下减小计算步长对计算量的影响是很大的。从物理图象上说，晶体原子做周期性运动，特征时间应为其振动周期，那么计算步长应该更小才合理。一般而言，晶体分子振动周期约为100fs量级，那么所取的1fs完全满足精度条件，甚至还可以放的更粗略一些。

转到目标文件夹下，输入命令开始计算：

计算结果

最终的计算结果储存在dump.lammpstrj中，包括包括预览视图和文本视图，每个计算过程各个原子的位置都能计算并呈现。

在计算过程中，命令行也会每100次展现计算结果，我们重点观察体积项。由于在一级相变过程中存在体积突变，因此我们可以据此寻找计算的一级相变点，在选取的温度范围内应为固液相变的熔点。

关键数据在下图展示：

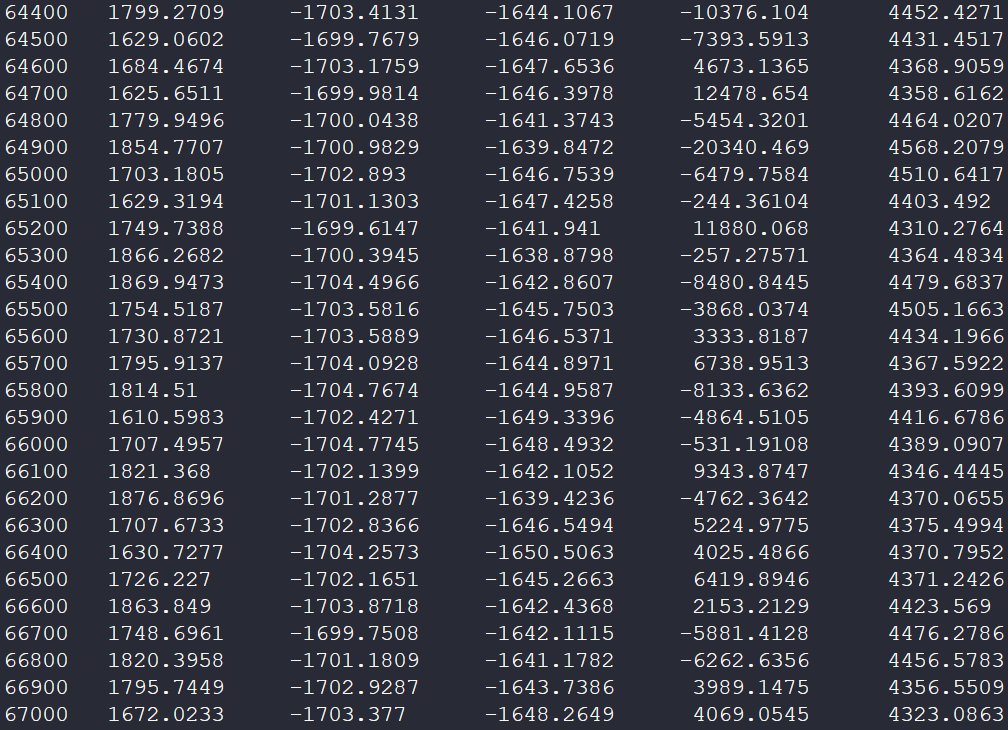
可以发现在1800K左右前后计算的晶体体积相差很大，说明计算结果认为熔点在1800K附近。当然可以根据dump.lammpstrj文件得到更全面的结果。我们需要批量提取数据的python文件：

各文件和输出结果已附加在数据集中。