新建
"高性能跨平台临近表实现" - 算法介绍 及 Python示例
yifeng_zhao
推荐镜像 :Basic Image:bohrium-notebook:2023-04-07
推荐机型 :c2_m4_cpu
赞 1
3
2
目录
©️ Copyright 2023 @ Authors
作者：浙江大学&西湖大学M3 Lab 赵益峰 📨
最后更新日期：2023-09-28
AI4Science 第三届Hackathon挑战 硬核软件开发赛道
共享协议：本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。
📖 上手指南
本文档可在 Bohrium Notebook 上直接运行。你可以点击界面上方按钮
开始连接，选择 bohrium-notebook:2023-04-07 镜像及 c2_m4_cpu 节点配置，稍等片刻即可运行。
代码
文本
一、介绍
代码
文本
临近表介绍
在计算科学和工程领域，临近表（Neighbor List, NBL）是一种重要的数据结构和算法，用于解决各种与空间关联和邻近性有关的问题。 临近表的核心概念涉及到一个目标对象的集合（例如，在分子模拟中，这可能是一组分子的坐标集合），以及从这些对象中抽象而来的邻居关系对应关系。
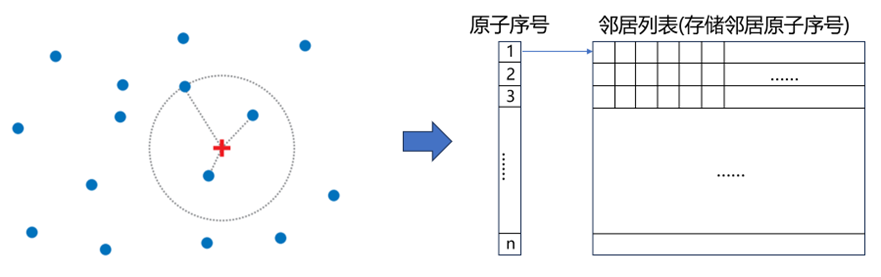
图1 示例点集及临近表提供的对应关系
直观上，临近表可以通过循环遍历目标对象集合来实现，以检查每个对象与其他对象之间的空间关系。然而，随着目标对象数量的增加，这种简单的循环遍历会导致时间复杂度指数爆炸，从而使计算变得非常耗时和低效。因此，为了提高效率，临近表的实现通常会采用更复杂的数据结构和算法。
从应用角度而言，临近表在分子模拟、流体动力学、颗粒模拟、计算机图形学等领域中扮演着至关重要的角色，建立一个跨平台的高效通用架构以为不同领域的研究人员提供统一的工具，促进知识交流和跨领域合作，同时也降低了开发和维护多个专门架构的成本，为科学和工程的创新提供便利。
代码
文本
主要应用场景和解决方案
在临近表的主要应用场景中，我们面临着不同类型的空间。首先是稠密空间，它涉及到在特定区域内，对象或实体之间的距离较小，相对于空间的总体范围，对象数量相对较多，它们密集地堆积在一起，形成连续的分布。其次是稀疏空间，指的是在特定区域内，对象或实体之间的距离较大，相对于空间的总体范围，对象数量相对较少。此外，还存在一类具有不同大小颗粒的空间，通过一些技术，如stencil模板、动态调整等，可以将其归类为前两种空间类型之一。
图2 主要应用场景
代码
文本
二、 算法细节
代码
文本
基于网格实现的临近表 - Grid-based NBL
在介绍Grid-based NBL之前，让我们设想一下最直觉的NBL实现: 考虑一个二维平面上的粒子系统，其中有许多粒子散布在空间中，构建邻居关系，只需要遍历邻居粒子，此时也就是所有粒子，然后检验特征距离，判断是否满足邻居关系的条件，例如欧式距离等。显然，该直觉的NBL实现具有O(n^2)时间复杂度，随着粒子数量的增加，计算成本将急剧增加。
在此基础上，理解Grid-based NBL其实简单了。它的核心思想就是将空间划分为网格单元，并将每个粒子被放置在对应的网格单元中，然后在遍历邻居粒子时，我们只需遍历粒子所在网格单元的邻居单元中的粒子即可，之后检验特征距离的过程是相同的。这样可以大大减少所需遍历的邻居粒子，实现效率的提升。
图3 通过对空间的划分，实现计算效率的显著提升
具体步骤如下图所示，包含三个主要步骤：划分网格，构建颗粒-网格关系，基于网格的相邻关系的颗粒临近表构建。
图4 Grid-based NBL的构建方法
代码
文本
基于八叉树实现的临近表 - Octree NBL
在上述的Grid-based NBL中，通过Grid空间划分可以显著减少处理大规模粒子系统时计算成本，但它仍然存在一些限制，尤其在处理稀疏空间的情况下。在稀疏空间中，粒子的分布可能不均匀，均匀的Grid空间划分，会导致某些网格单元中有很少或没有粒子，而其他网格单元可能非常拥挤，这会导致了计算效率的浪费，特别是对于高维度或大规模的粒子系统，Grid-based NBL需要大量的内存来存储网格单元数据结构，进而影响性能。
图5 两种空间划分的示意图
为了克服Grid-based NBL的限制，Octree NBL应运而生。它与Grid NBL的主要区别在于空间划分的形式以及邻居粒子的遍历方法。Octree NBL的空间划分不仅仅与颗粒的位置有关，还与颗粒的数量密切相关。在具体的实现中，我们以四个颗粒为基准，构建多个耦合体，递归地形成一个树状结构。同时，这个树结构的构建会根据颗粒的位置和聚集密度动态地进行调整。这种划分策略会根据颗粒的分布情况，在颗粒数量较密集的区域增加划分的网格密度，而在稀疏的区域进行相应的调整。此外，Octree NBL的邻居粒子遍历也充分考虑了树结构的特点。通过适当的减枝策略，Octree NBL可以忽略掉一些不想关子树对应的空间，更快速地定位具有相近空间位置的颗粒，从而提高搜索效率。
Octree NBL的具体构建过程如下图所示：
图6 Octree NBL的构建方法
代码
文本
基于Hash实现的临近表 - Hash NBL
通过以上两种临近表的介绍，我们可以注意到它们的核心思想都是通过空间划分或树结构的构建等映射方法，来建立目标对象之间的相邻关系。随后，利用这种相邻关系，减少所需遍历的邻居颗粒，从而实现了邻近表的高效构建。基于该思路，我们尝试构建了一个函数，来直接计算对象的相邻关系，并以此来构建临近表。以三维问题为例，这个函数具有以下三个特征：1. 维度变换：能够把三维空间点映射为能够容易操作的一维线性数据。2. 保持相邻关系：映射后的一维数据保有与三维空间相同的邻居关系。3. 计算廉价。
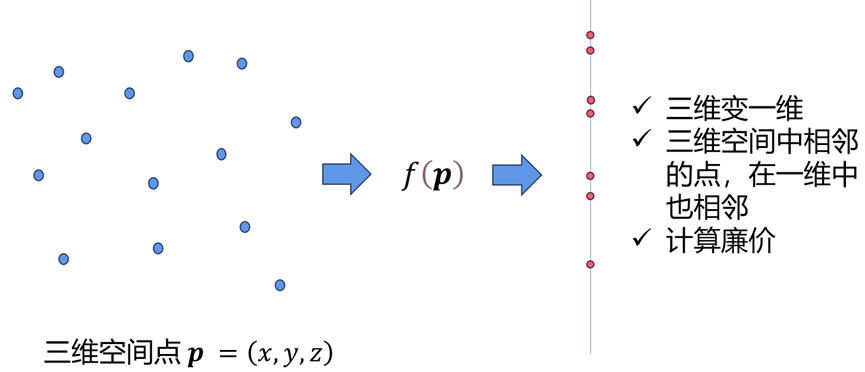
图7 Hash NBL的设想
由于在Hash NBL中，邻居关系可以通过Hash函数直接计算得到，无需依赖空间划分，因此从理论上来说，它具备最高的计算效率。
代码
文本
三、 基于Python的实现示例
代码
文本
为方便大家更好地理解上述三种临近表，此处提供了基于Python的实现。
代码
文本
Grid-based NBL
代码
文本
[ ]
import numpy as np
class GB_NBL_cube:
def __init__(self, cube_size, num_particles, cut_off_radius):
self.cube_size = np.array(cube_size) # cube的大小
# cube离散化后的cell数量
self.lc = np.array(cube_size) / np.array(cut_off_radius)
self.rc = cut_off_radius # cut off radius
self.num_particles = num_particles # 空间中颗粒的数量
# grid_size = cube_size / (cube_size / rc)
self.grid_size = np.array(cube_size) / (self.lc)
# 计算总cell数量，此处不考虑ghost_cell
self.num_cells = int(self.lc[0] * self.lc[1] * self.lc[2])
# 表示颗粒的邻接关系
self.particle_list = []
# 表示cell间的邻接关系
self.cell_list = []
def _xyz2ind(self, xyz):
"""
将坐标转换为对应的 cell 索引
参数:
- xyz: 三维坐标 (NumPy array 或单个值)
返回:
- cell_index: 对应的 cell 索引 (NumPy array 或单个值)
"""
xyz = np.atleast_2d(xyz)
# 将坐标限制在周期性边界内
xyz = np.remainder(xyz, self.cube_size)
cell_index = np.floor_divide(xyz, self.grid_size)
cell_index = cell_index[:, 0] * self.lc[1] * self.lc[2] + cell_index[:, 1] * self.lc[2] + cell_index[:, 2]
cell_index = cell_index.astype(int)
if len(cell_index) == 1:
return cell_index[0]
return cell_index
def _ind2xyz(self, ind):
"""
将 cell 索引转换为对应的中心坐标
参数:
- ind: cell 索引 (NumPy array 或单个值)
返回:
- xyz: 对应的坐标 (NumPy array 或单个值)
"""
ind = np.atleast_1d(ind)
x = ind // (self.lc[1] * self.lc[2]) * self.grid_size[0] + self.grid_size[0] / 2
y = (ind // self.lc[2]) * self.grid_size[1] + self.grid_size[1] / 2
z = ind % self.lc[2] * self.grid_size[2] + self.grid_size[2] / 2
xyz = np.column_stack((x % self.cube_size[0], y % self.cube_size[1], z % self.cube_size[2]))
if len(xyz) == 1:
return xyz[0]
return xyz
def _get_min_diff(self, xyz1, xyz2):
"""
计算考虑周期边界的颗粒间最小距离
参数:
- xyz1: 第一个颗粒的坐标 (NumPy array 或单个值)
- xyz2: 第二个颗粒的坐标 (NumPy array 或单个值)
返回:
- distance: 考虑周期边界的最小镜像距离 (NumPy array 或单个值)
"""
difference = xyz2 - xyz1
difference = np.remainder(difference + self.cube_size / 2, self.cube_size) - self.cube_size / 2
return difference
def constructor(self, inputs):
# 初始化 self.particle_list， self.cell_list
self.particle_list = [[] for _ in range(self.num_particles)]
self.cell_list = [[] for _ in range(self.num_cells)]
# 把所有粒子都添加到对应的 cell 中
particle_inds = self._xyz2ind(inputs)
for particle_seq, particle_ind in enumerate(particle_inds):
self.cell_list[particle_ind].append(particle_seq)
# 建立链接关系, 考虑rc
for particle_seq, xyz in enumerate(inputs):
particle_ind = particle_inds[particle_seq]
adjacent_cells = self.get_neighbor_cells(particle_ind)
for cell_temp in adjacent_cells:
neighbor_particles_temp = self.cell_list[cell_temp]
if neighbor_particles_temp:
for neighbor_particle in neighbor_particles_temp:
if neighbor_particle == particle_seq:
continue
neighbor_xyz = inputs[neighbor_particle]
distance = np.linalg.norm(self._get_min_diff(xyz, neighbor_xyz))
# print(f"particle seq: {particle_seq}, particle neighbor: {neighbor_particle}, diff: {self._get_min_diff(xyz, neighbor_xyz)}, distance: {distance}")
if distance - self.rc <= 1e-10:
self.particle_list[particle_seq].append(neighbor_particle)
def get_neighbor_cells(self, cell_ind):
"""
给定一个 cell 索引，返回其 26 个相邻的 cell 索引，考虑周期性边界条件
参数:
- cell_ind: 给定的 cell 索引
- lc: cell 的离散化数量 (NumPy array)
返回:
- adjacent_cells: 26 个相邻的 cell 索引列表 及 自己本身
"""
i, j, k = self._ind2xyz(np.array(cell_ind))
adjacent_cells = []
for di in [-1, 0, 1]:
for dj in [-1, 0, 1]:
for dk in [-1, 0, 1]:
ni = (i + di * self.grid_size[0])
nj = (j + dj * self.grid_size[1])
nk = (k + dk * self.grid_size[2])
xyz_temp = np.column_stack((ni, nj, nk))
ind_temp = self._xyz2ind(xyz_temp)
adjacent_cells.append(ind_temp)
return set(adjacent_cells)
def get_neighbors(self, particle_seq):
"""
获取给定颗粒序号的邻近颗粒列表
参数:
- particle_seq: 给定的颗粒序号
返回:
- neighbors: 邻近颗粒列表
"""
return self.particle_list[particle_seq]
代码
文本
OCtree NBL
代码
文本
[ ]
from collections import deque
class Octree_nbl:
def __init__(self, size, num_particles, cut_off_radius):
# self.cube_size = np.array(cube_size) # 立方体的大小
self.rc = cut_off_radius # 截断半径
self.num_particles = num_particles
self.center = size / 2
self.size = size # 总长
self.children = [None] * 8
self.positions = [] # 存储粒子位置的NumPy数组
self.particles = [] # neighborlist relatinoships
def insert(self, positions):
# 构建八叉树
for position in positions:
if len(self.positions) < 4:
self.positions.append(position)
else:
is_right = position > self.center
indices = np.sum((is_right) * (2 ** np.arange(3))) # 二进制法计算属于那个子树
if self.children[indices] is None:
child_center = self.center + (is_right - 0.5) * self.size / 2
self.children[indices] = Octree_nbl(child_center, self.size / 2, self.rc)
self.children[indices].insert(np.array([position]))
def constructor(self, positions):
self.insert(positions)
# 构建neighborlist
self.particles = []
for i in range(self.num_particles):
nb_particles_temp = self.query(positions[i])
self.particles.append(nb_particles_temp)
def query(self, position):
nearby_positions = []
# AABB接触法，判断是否进行查询
min_bound = self.center - np.array([self.size / 2, self.size / 2, self.size / 2])
max_bound = self.center + np.array([self.size / 2, self.size / 2, self.size / 2])
# 检查查询范围是否与格子边界有交集
intersects = np.all(min_bound <= position + self.rc) and np.all(max_bound >= position - self.rc)
if intersects: # 如果有交集，直接将节点内所有粒子添加到结果列表
for pos in self.positions:
if np.linalg.norm(pos - position) - self.rc <= 1e-5:
nearby_positions.append(pos)
for child in self.children:
if child is not None:
nearby_positions.extend(child.query(position))
return nearby_positions
def get_neighbors(self, particle_seq):
"""
获取给定颗粒序号的邻近颗粒列表
参数:
- particle_seq: 给定的颗粒序号
返回:
- neighbors: 邻近颗粒列表
"""
return self.particles[particle_seq]
代码
文本
Hash NBL
代码
文本
[ ]
import numpy as np
from collections import defaultdict
import time
def hash_function_float(point, coefficient):
x, y, z = point
# 将浮点坐标映射到整数坐标范围（例如，0到2^16 - 1）
# coefficient = 1.5 # 2^16 - 1
x_int = int(x * coefficient)
y_int = int(y * coefficient)
z_int = int(z * coefficient)
# 将整数坐标合并成一个一维哈希值，使用 Z-order curve 映射
combined = 0
for i in range(16): # 假设每个坐标分量都是 16 位
combined |= (x_int & 1) << (3 * i)
combined |= (y_int & 1) << (3 * i + 1)
combined |= (z_int & 1) << (3 * i + 2)
x_int >>= 1
y_int >>= 1
z_int >>= 1
return combined
class HB_NBL_cube:
def __init__(self, cube_size, num_particles, cut_off_radius):
"""
初始化哈希表邻接格子对象
参数:
- cube_size: 立方体的大小 (一个包含3个值的 NumPy array 或类似的列表)
- num_particles: 颗粒的数量 (整数)
- cut_off_radius: 截断半径，用于确定邻居关系 (浮点数)
"""
self.cube_size = np.array(cube_size) # 立方体的大小
self.rc = cut_off_radius # 截断半径
self.num_particles = num_particles
# 表示颗粒的邻接关系
self.particle_list = [[] for _ in range(num_particles)]
# 哈希表: hashed_value : particle_seq，使用defaultdict构建
self.hash_table = defaultdict(list)
self.hash_list = [[] for _ in range(num_particles)]
self.coefficient = 1 / (cut_off_radius / 2)
self.range_size = 350# 350
self.move_size = 1
def _cal_hash_code(self, inputs):
"""
计算颗粒的哈希值并构建哈希表
参数:
- inputs: 颗粒的坐标数据，一个大小为(num_particles, 3)的 NumPy array
"""
# # 非周期边界
# for i in range(self.num_particles):
# hash_code = hash_function_float(inputs[i], self.coefficient)
# print(inputs[i])
# hash_range = hash_code // self.range_size
# print(hash_code)
# print(hash_range)
# if not self.hash_table[hash_range * self.range_size]:
# self.hash_table[hash_range * self.range_size] = []
# self.hash_table[hash_range * self.range_size].append(i)
# print(hash_range * self.range_size)
# print("___________")
def add_to_hash_table(input_temp, index):
x, y, z = input_temp
input_list = [[x + self.move_size, y, z],
[x - self.move_size, y, z],
[x, y + self.move_size, z],
[x, y - self.move_size, z],
[x, y, z + self.move_size],
[x, y, z - self.move_size]]
hash_range_set = set() # 使用集合来存储唯一的哈希范围值
for value in input_list:
hash_code = hash_function_float(value, self.coefficient)
hash_range_temp = hash_code // self.range_size
hash_range_set.add(hash_range_temp * self.range_size) # 使用add()方法来添加唯一值
for hash_value in hash_range_set:
if not self.hash_table[hash_value]:
self.hash_table[hash_value] = []
self.hash_table[hash_value].append(index)
return hash_range_set # 返回集合
# # 周期边界
for i in range(self.num_particles):
hash_list_temp = []
hash_temp = add_to_hash_table(inputs[i], i)
hash_list_temp.extend(hash_temp)
if any(np.less(inputs[i], self.rc)) or any(np.greater(inputs[i], self.cube_size - self.rc)):
# 颗粒靠近边界，需要构建镜像
# 构建并添加周期边界镜像
for axis in range(3):
if inputs[i, axis] < self.rc:
mirrored_position = inputs[i].copy()
mirrored_position[axis] += self.cube_size[axis]
hash_temp = add_to_hash_table(mirrored_position, i)
hash_list_temp.extend(hash_temp)
if inputs[i, axis] > self.cube_size[axis] - self.rc:
mirrored_position = inputs[i].copy()
mirrored_position[axis] += self.rc
mirrored_position[axis] -= self.cube_size[axis]
hash_temp = add_to_hash_table(mirrored_position, i)
hash_list_temp.extend(hash_temp)
# print(hash_list_temp)
self.hash_list[i] = hash_list_temp
def _get_min_diff(self, xyz1, xyz2):
"""
计算考虑周期边界的颗粒间最小距离
参数:
- xyz1: 第一个颗粒的坐标 (NumPy array 或单个值)
- xyz2: 第二个颗粒的坐标 (NumPy array 或单个值)
返回:
- distance: 考虑周期边界的最小镜像距离 (NumPy array 或单个值)
"""
difference = xyz2 - xyz1
difference = np.remainder(difference + self.cube_size / 2, self.cube_size) - self.cube_size / 2
return difference
def constructor(self, inputs):
"""
构建哈希表和邻居列表，考虑截断半径
参数:
- inputs: 颗粒的坐标数据，一个大小为(num_particles, 3)的 NumPy array
"""
# 创建hash_code表
self._cal_hash_code(inputs)
for particle_seq, particle_xyz in enumerate(inputs):
particle_hash_values = self.hash_list[particle_seq]
for particle_hash_value in particle_hash_values:
# # particle_hash_range = particle_hash_value // self.range_size
# neighbor_particles = set()
# neighbor_particles.update(self.hash_table[particle_hash_value])
# neighbor_particles.update(self.hash_table[particle_hash_value + self.range_size])
# neighbor_particles.update(self.hash_table[particle_hash_value - self.range_size])
# neighbor_particles.update(self.hash_table[particle_hash_range * self.range_size])
# neighbor_particles.update(self.hash_table[(particle_hash_range + 1) * self.range_size])
# neighbor_particles.update(self.hash_table[(particle_hash_range - 1) * self.range_size])
# neighbor_particles.update(self.hash_table[(particle_hash_range + 2) * self.range_size])
# neighbor_particles.update(self.hash_table[(particle_hash_range - 2) * self.range_size])
neighbor_particles = self.hash_table[particle_hash_value]
for neighbor_particle_seq in neighbor_particles:
if neighbor_particle_seq <= particle_seq:
continue
if neighbor_particle_seq in self.particle_list[particle_seq]:
continue
distance = np.linalg.norm(self._get_min_diff(particle_xyz, inputs[neighbor_particle_seq]))
if distance <= self.rc:
self.particle_list[particle_seq].append(neighbor_particle_seq)
self.particle_list[neighbor_particle_seq].append(particle_seq)
def get_neighbors(self, particle_seq):
"""
获取给定颗粒序号的邻近颗粒列表
参数:
- particle_seq: 给定的颗粒序号
返回:
- neighbors: 邻近颗粒列表
"""
return self.particle_list[particle_seq]
代码
文本
四、测试
代码
文本
通过随机生成随机数，我们对上述python示例实现进行了测试
代码
文本
[ ]
print("较稀疏系统的测试结果：")
cube_size = np.array([10, 10, 10])
num_particles = 50 # 平台算力有限，建议不要取太大
cut_off_radius = 1.0
grid_lc_cube = GB_NBL_cube(cube_size, num_particles, cut_off_radius)
octree_lc_cube = Octree_nbl(cube_size, num_particles, cut_off_radius)
h_lc_cube = HB_NBL_cube(cube_size, num_particles, cut_off_radius)
# 生成测试数据
np.random.seed(1)
inputs = np.random.random((num_particles, 3)) * cube_size
print("随机生成的输入数据:")
print(inputs)
######################################
# Grid-basd NBL
# 记录开始时间
start_time = time.time()
# 调用 constructor 方法进行初始化
grid_lc_cube.constructor(inputs)
# 计算代码执行所需的时间
elapsed_time = time.time() - start_time
print(f"代码执行耗时: {elapsed_time} 秒")
######################################
# Octree NBL
# 记录开始时间
start_time = time.time()
# 调用 constructor 方法进行初始化
octree_lc_cube.constructor(inputs)
# 计算代码执行所需的时间
elapsed_time = time.time() - start_time
print(f"代码执行耗时: {elapsed_time} 秒")
######################################
# Hash NBL
# 记录开始时间
start_time = time.time()
# 调用 constructor 方法进行初始化
h_lc_cube.constructor(inputs)
# 计算代码执行所需的时间
elapsed_time = time.time() - start_time
print(f"代码执行耗时: {elapsed_time} 秒")
代码
文本
[ ]
print("较稠密系统的测试结果：")
cube_size = np.array([10, 10, 10])
num_particles = 1000 # 平台算力有限，建议不要取太大
cut_off_radius = 1.0
grid_lc_cube = GB_NBL_cube(cube_size, num_particles, cut_off_radius)
octree_lc_cube = Octree_nbl(cube_size, num_particles, cut_off_radius)
h_lc_cube = HB_NBL_cube(cube_size, num_particles, cut_off_radius)
# 生成测试数据
np.random.seed(1)
inputs = np.random.random((num_particles, 3)) * cube_size
print("随机生成的输入数据:")
print(inputs)
######################################
# Grid-basd NBL
# 记录开始时间
start_time = time.time()
# 调用 constructor 方法进行初始化
grid_lc_cube.constructor(inputs)
# 计算代码执行所需的时间
elapsed_time = time.time() - start_time
print(f"代码执行耗时: {elapsed_time} 秒")
######################################
# Octree NBL
# 记录开始时间
start_time = time.time()
# 调用 constructor 方法进行初始化
octree_lc_cube.constructor(inputs)
# 计算代码执行所需的时间
elapsed_time = time.time() - start_time
print(f"代码执行耗时: {elapsed_time} 秒")
######################################
# Hash NBL
# 记录开始时间
start_time = time.time()
# 调用 constructor 方法进行初始化
h_lc_cube.constructor(inputs)
# 计算代码执行所需的时间
elapsed_time = time.time() - start_time
print(f"代码执行耗时: {elapsed_time} 秒")
代码
文本
五、结论
代码
文本
可以发现这三种NBL在不同的系统中表现各异，Grid NBL在稠密系统中表现良好，但由于在稀疏系统中会划分较多的空网格，造成了性能下降；Octree NBL的表现恰与此相反；而Hash NBL则在两类系统中都保持了较好且稳定的表现，基本实现了设计目的。
代码
文本
已赞1
本文被以下合集收录
AI4S
凝聚态平方
更新于 2024-03-18
32 篇0 人关注
计算材料学
hjchen
更新于 2023-10-12
24 篇0 人关注
推荐阅读
公开
《计算材料学》（分子动力学）LAMMPS实例
JH_Wang
更新于 2024-07-18
4 赞5 转存文件
公开
一篇带你了解 Bohrium Notebook 的使用
Hui_Zhou
发布于 2023-11-24
3 赞