

决策树与可解释性|决策树(Decision Tree)在材料学中的应用
1. 决策数简介
引言:
决策树()是一种非参数的有监督学习方法,它能够从一系列有特征和标签的数据中总结出决策规则,并用树状图的结构来呈现这些规则,以解决分类和回归问题。它们从根节点开始,通过分裂属性将数据分割成较小的子集,直至叶节点,每个叶节点代表一个预测结果。
决策树算法容易理解,适用各种数据,在解决各种问题时都有良好表现,尤其是以树模型为核心的各种集成算法,在各个行业和领域都有广泛的应用。
决策树的特点:
决策树的优点包括模型的直观性和可解释性。然而,它们也容易过拟合,即模型在训练数据上表现很好但在新数据上表现差。为了防止过拟合,可以采用剪枝技术。
在回归问题中,决策树能够预测连续值。在材料科学中,决策树可以用于发现新材料的潜在属性或预测材料性能。
Python的sklearn库提供了决策树算法的实现,支持分类(DecisionTreeClassifier)和回归(DecisionTreeRegressor)问题。
本教程AIMS:
本教程将使用一个材料科学中的数据,用决策树算法对材料进行分类并总结分类规则。
- 掌握如何使用 sklearn 建立决策树模型,理解参数、属性、接口
- 分类树重要属性和参数|建立一棵树
- 回归树剪枝与可视化
- 通过绘制决策树图
Reference:
- Suwarno, S.; Dicky, G.; Suyuthi, A.; Effendi, M.; Witantyo, W.; Noerochim, L.; Ismail, M. Machine Learning Analysis of Alloying Element Effects on Hydrogen Storage Properties of AB2 Metal Hydrides. Int. J. Hydrogen Energy 2022, 47 (23), 11938–11947. https://doi.org/10.1016/j.ijhydene.2022.01.210.
案例背景
向清洁和可持续能源的过渡以克服对日益稀缺的化石燃料的依赖,是可持续发展的基础。氢能是一种很有前途的能源载体,可以燃料电池的形式转化为电能。氢的能量密度约为 ,大大高于标准化石燃料(),同时在燃烧过程中只产生水蒸气作为副产品,清洁无污染。然而,需要储氢设备来向燃料电池供应氢,这限制了氢能的应用。轻型燃料电池汽车需要大约 的氢气才能行驶 公里。但在环境温度和大气压下, 气体形式的氢气将占据 的体积。因此,目前正进行许多研究以实现高容量储氢。
常用的储氢方法有高压气瓶储氢、低温液态储氢和固体材料储氢。高压气瓶储氢具有最高的储氢容量,但需要在非常高的压力()下可用,这带来了安全问题,低温液态储氢同样不适合在室温下使用。相比之下,储氢合金可吸收氢气形成金属氢化物,其在晶格间隙位置上吸收的氢能够在室温和大气压下储存,同时又兼具有较高的储氢容量,因而成为有前途的储氢方式。
金属氢化物可分为离子氢化物、共价氢化物和金属间氢化物。金属间氢化物被认为是其中最有前途的储氢材料。金属间氢化物被表征为五个金属氢化物家族,即 和 。在这些家族中, 金属氢化物显示出突出的储氢和电池应用的潜力。其中元素 可由第 族元素(、 和 )或镧系元素( 和 )形成,而 可由过渡和非过渡金属形成,如 和 。 合金结晶为立方 或六方 结构的 相晶体。这取决于合金成分,特别是元素的外部电子密度和原子尺寸。立方相因具有更高的晶格空隙率,一般具有更高的储氢容量。
在这里,我们收集并整理了 1998 年至 2019 年发表的储氢合金储氢容量研究的数据。建立了 模型,将 合金的化学组成与储氢性质联系起来,即生成热()、立方相丰度 ()和氢重量百分比(%)。该模型旨在获得合金元素在储氢性能中的作用的新见解,并可用于研究人员指导他们的实验工作。
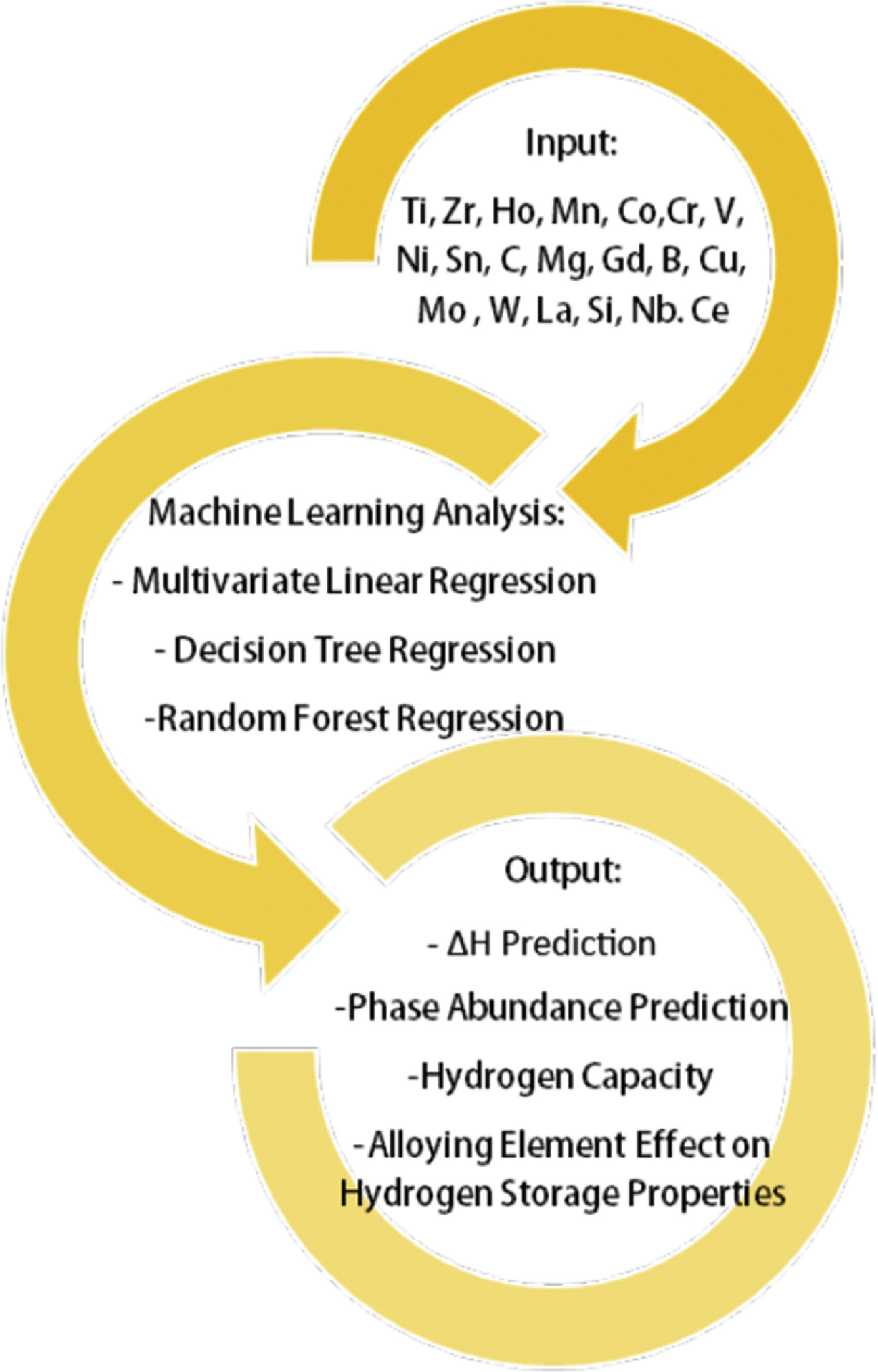
数据集介绍
本数据集针对 合金金属氢化物的储氢性能,首先提供了 个不同合金的储氢性质数据。这些数据包含在文件 “AB2_Hydrogen.xlsx" 表中。
- 表第一列为数据来源参考文献的序号
- 第 ~ 列给出了吸氢合金各元素 ( ) 含量,以原子比例形式给出
- 第 , , 列给出了合金中B、A的含量和比例;
- 第 ,给出了该金属氢化物反应的生成热( )和熵变( )
- 第 , 列给出了该金属氢化物反应的立方相丰度 ()和六方相丰度 ()
- 第 列给出了氢重量百分比(%)。
本文将使用合金元素作为特征,金属氢化物的生成焓ΔH作为标签
2 分类树(DecisionTreeClassifier)
- 代码示例:
classsklearn.tree.DecisionTreeClassifier(criterion=’gini’, splitter=’best’, max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, class_weight=None, presort=False)
DecisionTreeClassifier 是 sklearn 库中用于分类问题的决策树模型。它通过构建一棵决策树来预测样本的类别。模型的主要参数包括:
criterion:衡量分裂质量的函数,常用的有 "gini"(基尼不纯度)和 "entropy"(信息增益)。splitter:选择分裂节点的策略,"best" 表示选择最优分裂,"random" 表示随机分裂。max_depth:树的最大深度,用来控制过拟合。min_samples_split:分裂内部节点所需的最小样本数。min_samples_leaf:叶节点所需的最小样本数,也是用来控制过拟合的重要参数。max_features:寻找最佳分裂时考虑的特征数量。random_state:控制随机性的种子值。
决策树的优点在于模型易于理解,可视化展示决策过程,但也容易过拟合,特别是当树太深时。通过调整参数,比如增加 min_samples_split 或设置 max_depth,可以帮助减轻过拟合问题。
2.1 重要参数
2.1.1 criterion 参数与创建决策树模型
为了要将表格转化为一棵树,决策树需要找出最佳节点和最佳的分枝方法,对分类树来说,衡量这个“最佳”的指标叫做“不纯度”。通常来说,不纯度越低,决策树对训练集的拟合越好。现在使用的决策树算法在分枝方法上的核心大多是围绕在对某个不纯度相关指标的最优化上。
不纯度基于节点来计算,树中的每个节点都会有一个不纯度,并且子节点的不纯度一定是低于父节点的,也就是说,在同一棵决策树上,叶子节点的不纯度一定是最低的。
Criterion这个参数正是用来决定不纯度的计算方法的。sklearn提供了两种选择:
1)输入”“,使用信息熵(Entropy) 2)输入”“,使用基尼系数(Gini Impurity) 其中 代表给定的节点, 代表标签的任意分类, 代表标签分类 在节点 上所占的比例。注意,当使用信息熵时,sklearn 实际计算的是基于信息熵的信息增益(),即父节点的信息熵和子节点的信息熵之差。
比起基尼系数,信息熵对不纯度更加敏感,对不纯度的惩罚最强。但是 在实际使用中,信息熵和基尼系数的效果基本相同。信息熵的计算比基尼系数缓慢一些,因为基尼系数的计算不涉及对数。另外,因为信息熵对不纯度更加敏感,所以信息熵作为指标时,决策树的生长会更加“精细”,因此对于高维数据或者噪音很多的数据,信息熵很容易过拟合,基尼系数在这种情况下效果往往比较好。当然,这不是绝对的。
| 参数 | criterion |
|---|---|
| 如何影响模型? | 确定不纯度的计算方法,帮忙找出最佳节点和最佳分枝,不纯度越低,决策树对训练集的拟合越好 |
| 可能的输入有哪些? | 不填默认基尼系数,填写gini使用基尼系数,填写entropy使用信息增益 |
| 怎样选取参数? | 通常就使用基尼系数,数据维度很大,噪音很大时使用基尼系数 维度低,数据比较清晰的时候,信息熵和基尼系数没区别 当决策树的拟合程度不够的时候,使用信息熵 两个都试试,不好就换另外一个 |
决策树的基本流程简单概括如下:
- 计算全部特征的不纯度指标 →
- 选取不纯度指标最优的特征来分枝 →
- 进行第一个特征分枝后,计算全部特征的不纯度指标 →
- 选取不纯度指标最优的特征继续分枝……
- 在创建决策树之前,我们先导入数据
A. 导入数据集和需要的模块
| Journal | Ti | Zr | Mn | Co | Cr | V | Ni | Sn | Al | ... | Ce | Y | B | A | B/A | ΔH | ΔS | C14 | C15 | wt% | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1.000000 | 0.000000 | 0.850000 | 0.000000 | 1.000000 | 0.050000 | 0.000000 | 0.0 | 0.000000 | ... | 0.0 | 0.0 | 2.0 | 1.0 | 2.0 | 14.70 | 93.7 | 100.0 | 0.0 | NaN |
| 1 | 1 | 1.000000 | 0.000000 | 0.700000 | 0.000000 | 1.000000 | 0.100000 | 0.000000 | 0.0 | 0.000000 | ... | 0.0 | 0.0 | 2.0 | 1.0 | 2.0 | 17.70 | 101.0 | 100.0 | 0.0 | NaN |
| 2 | 1 | 1.000000 | 0.000000 | 0.550000 | 0.000000 | 1.000000 | 0.150000 | 0.000000 | 0.0 | 0.000000 | ... | 0.0 | 0.0 | 2.0 | 1.0 | 2.0 | 18.60 | 99.9 | 100.0 | 0.0 | NaN |
| 3 | 1 | 1.000000 | 0.000000 | 0.400000 | 0.000000 | 1.000000 | 0.200000 | 0.000000 | 0.0 | 0.000000 | ... | 0.0 | 0.0 | 2.0 | 1.0 | 2.0 | 20.20 | 103.0 | 100.0 | 0.0 | NaN |
| 4 | 1 | 0.959596 | 0.040404 | 1.000000 | 0.000000 | 1.000000 | 0.000000 | 0.000000 | 0.0 | 0.000000 | ... | 0.0 | 0.0 | 2.0 | 1.0 | 2.0 | 15.10 | 93.0 | 100.0 | 0.0 | NaN |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 309 | 50 | 0.357798 | 0.642202 | 0.132653 | 0.132653 | 0.125000 | 0.173469 | 0.522959 | 0.0 | 0.017857 | ... | 0.0 | 0.0 | 2.0 | 1.0 | 2.0 | 36.82 | 110.0 | 0.0 | 0.0 | 1.27 |
| 310 | 50 | 0.356863 | 0.643137 | 0.163539 | 0.163539 | 0.152815 | 0.214477 | 0.640751 | 0.0 | 0.021448 | ... | 0.0 | 0.0 | 2.0 | 1.0 | 2.0 | 36.72 | 110.0 | 0.0 | 0.0 | 1.33 |
| 311 | 50 | 0.358650 | 0.641350 | 0.146982 | 0.146982 | 0.139108 | 0.194226 | 0.577428 | 0.0 | 0.018373 | ... | 0.0 | 0.0 | 2.0 | 1.0 | 2.0 | 37.03 | 110.0 | 0.0 | 0.0 | 1.38 |
| 312 | 50 | 0.360784 | 0.639216 | 0.163539 | 0.166220 | 0.155496 | 0.214477 | 0.651475 | 0.0 | 0.021448 | ... | 0.0 | 0.0 | 2.0 | 1.0 | 2.0 | 34.83 | 110.0 | 0.0 | 0.0 | 1.24 |
| 313 | 50 | 0.359833 | 0.640167 | 0.152231 | 0.149606 | 0.139108 | 0.196850 | 0.590551 | 0.0 | 0.020997 | ... | 0.0 | 0.0 | 2.0 | 1.0 | 2.0 | 36.53 | 110.0 | 0.0 | 0.0 | 1.42 |
314 rows × 31 columns
B. 数据预处理:删除数据量过少的元素
我将选择作为要预测的标签,初步设置为大于等于 的是放热(标记为 ),小于 的是不放热(标记为 )。
Index(['Journal', 'Ti', 'Zr', 'Mn', 'Co', 'Cr', 'V', 'Ni', 'Sn', 'Al', 'C',
'Mg', 'Gd', 'Fe', 'B (Boron)', 'Cu', 'Mo', 'W', 'La', 'Si', 'Nb', 'Ce',
'Y', 'B', 'A', 'B/A', 'ΔH', 'ΔS', 'C14', 'C15', 'wt%'],
dtype='object')| Journal | Ti | Zr | Mn | Co | Cr | V | Ni | Sn | Al | ... | Y | B | A | B/A | ΔH | ΔS | C14 | C15 | wt% | exothermic | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1.000000 | 0.000000 | 0.850000 | 0.000000 | 1.000000 | 0.050000 | 0.000000 | 0.0 | 0.000000 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 14.70 | 93.7 | 100.0 | 0.0 | NaN | 0.0 |
| 1 | 1 | 1.000000 | 0.000000 | 0.700000 | 0.000000 | 1.000000 | 0.100000 | 0.000000 | 0.0 | 0.000000 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 17.70 | 101.0 | 100.0 | 0.0 | NaN | 0.0 |
| 2 | 1 | 1.000000 | 0.000000 | 0.550000 | 0.000000 | 1.000000 | 0.150000 | 0.000000 | 0.0 | 0.000000 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 18.60 | 99.9 | 100.0 | 0.0 | NaN | 0.0 |
| 3 | 1 | 1.000000 | 0.000000 | 0.400000 | 0.000000 | 1.000000 | 0.200000 | 0.000000 | 0.0 | 0.000000 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 20.20 | 103.0 | 100.0 | 0.0 | NaN | 0.0 |
| 4 | 1 | 0.959596 | 0.040404 | 1.000000 | 0.000000 | 1.000000 | 0.000000 | 0.000000 | 0.0 | 0.000000 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 15.10 | 93.0 | 100.0 | 0.0 | NaN | 0.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 309 | 50 | 0.357798 | 0.642202 | 0.132653 | 0.132653 | 0.125000 | 0.173469 | 0.522959 | 0.0 | 0.017857 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 36.82 | 110.0 | 0.0 | 0.0 | 1.27 | 0.0 |
| 310 | 50 | 0.356863 | 0.643137 | 0.163539 | 0.163539 | 0.152815 | 0.214477 | 0.640751 | 0.0 | 0.021448 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 36.72 | 110.0 | 0.0 | 0.0 | 1.33 | 0.0 |
| 311 | 50 | 0.358650 | 0.641350 | 0.146982 | 0.146982 | 0.139108 | 0.194226 | 0.577428 | 0.0 | 0.018373 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 37.03 | 110.0 | 0.0 | 0.0 | 1.38 | 0.0 |
| 312 | 50 | 0.360784 | 0.639216 | 0.163539 | 0.166220 | 0.155496 | 0.214477 | 0.651475 | 0.0 | 0.021448 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 34.83 | 110.0 | 0.0 | 0.0 | 1.24 | 0.0 |
| 313 | 50 | 0.359833 | 0.640167 | 0.152231 | 0.149606 | 0.139108 | 0.196850 | 0.590551 | 0.0 | 0.020997 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 36.53 | 110.0 | 0.0 | 0.0 | 1.42 | 0.0 |
314 rows × 32 columns
Ti 30 Zr 38 Mn 53 Co 178 Cr 82 V 95 Ni 156 Sn 225 Al 203 C 313 Mg 308 Gd 313 Fe 207 B (Boron) 305 Cu 309 Mo 304 W 311 La 298 Si 309 Nb 312 Ce 313 Y 290 dtype: int64
经过统计,发现数据中存在一些大部分合金都不含有的元素,因此在训练决策树之前我们先对数据进行预处理,删掉绝大多数合金中含量为0的元素。这里我们以 Y 金属(在 个合金数据中含量为 )作为分界点。
Index(['C', 'Mg', 'Gd', 'B (Boron)', 'Cu', 'Mo', 'W', 'La', 'Si', 'Nb', 'Ce'], dtype='object')
如上图所示,以金属 Y 为分界金属,可从特征元素中将含量较少的金属元素剔除。
要删除的元素 ['C', 'Mg', 'Gd', 'B (Boron)', 'Cu', 'Mo', 'W', 'La', 'Si', 'Nb', 'Ce'] -------------------------------------------------------------------------------- 删除后的数据
| Journal | Ti | Zr | Mn | Co | Cr | V | Ni | Sn | Al | ... | Y | B | A | B/A | ΔH | ΔS | C14 | C15 | wt% | exothermic | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1.000000 | 0.000000 | 0.850000 | 0.000000 | 1.000000 | 0.050000 | 0.000000 | 0.0 | 0.000000 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 14.70 | 93.7 | 100.0 | 0.0 | NaN | 0.0 |
| 1 | 1 | 1.000000 | 0.000000 | 0.700000 | 0.000000 | 1.000000 | 0.100000 | 0.000000 | 0.0 | 0.000000 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 17.70 | 101.0 | 100.0 | 0.0 | NaN | 0.0 |
| 2 | 1 | 1.000000 | 0.000000 | 0.550000 | 0.000000 | 1.000000 | 0.150000 | 0.000000 | 0.0 | 0.000000 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 18.60 | 99.9 | 100.0 | 0.0 | NaN | 0.0 |
| 3 | 1 | 1.000000 | 0.000000 | 0.400000 | 0.000000 | 1.000000 | 0.200000 | 0.000000 | 0.0 | 0.000000 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 20.20 | 103.0 | 100.0 | 0.0 | NaN | 0.0 |
| 4 | 1 | 0.959596 | 0.040404 | 1.000000 | 0.000000 | 1.000000 | 0.000000 | 0.000000 | 0.0 | 0.000000 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 15.10 | 93.0 | 100.0 | 0.0 | NaN | 0.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 309 | 50 | 0.357798 | 0.642202 | 0.132653 | 0.132653 | 0.125000 | 0.173469 | 0.522959 | 0.0 | 0.017857 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 36.82 | 110.0 | 0.0 | 0.0 | 1.27 | 0.0 |
| 310 | 50 | 0.356863 | 0.643137 | 0.163539 | 0.163539 | 0.152815 | 0.214477 | 0.640751 | 0.0 | 0.021448 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 36.72 | 110.0 | 0.0 | 0.0 | 1.33 | 0.0 |
| 311 | 50 | 0.358650 | 0.641350 | 0.146982 | 0.146982 | 0.139108 | 0.194226 | 0.577428 | 0.0 | 0.018373 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 37.03 | 110.0 | 0.0 | 0.0 | 1.38 | 0.0 |
| 312 | 50 | 0.360784 | 0.639216 | 0.163539 | 0.166220 | 0.155496 | 0.214477 | 0.651475 | 0.0 | 0.021448 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 34.83 | 110.0 | 0.0 | 0.0 | 1.24 | 0.0 |
| 313 | 50 | 0.359833 | 0.640167 | 0.152231 | 0.149606 | 0.139108 | 0.196850 | 0.590551 | 0.0 | 0.020997 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 36.53 | 110.0 | 0.0 | 0.0 | 1.42 | 0.0 |
314 rows × 21 columns
C. 划分训练集和测试集
| Journal | Ti | Zr | Mn | Co | Cr | V | Ni | Sn | Al | ... | Y | B | A | B/A | ΔH | ΔS | C14 | C15 | wt% | exothermic | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1.000000 | 0.000000 | 0.850000 | 0.000000 | 1.000000 | 0.050000 | 0.000000 | 0.0 | 0.000000 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 14.70 | 93.7 | 100.0 | 0.0 | NaN | 0.0 |
| 1 | 1 | 1.000000 | 0.000000 | 0.700000 | 0.000000 | 1.000000 | 0.100000 | 0.000000 | 0.0 | 0.000000 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 17.70 | 101.0 | 100.0 | 0.0 | NaN | 0.0 |
| 2 | 1 | 1.000000 | 0.000000 | 0.550000 | 0.000000 | 1.000000 | 0.150000 | 0.000000 | 0.0 | 0.000000 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 18.60 | 99.9 | 100.0 | 0.0 | NaN | 0.0 |
| 3 | 1 | 1.000000 | 0.000000 | 0.400000 | 0.000000 | 1.000000 | 0.200000 | 0.000000 | 0.0 | 0.000000 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 20.20 | 103.0 | 100.0 | 0.0 | NaN | 0.0 |
| 4 | 1 | 0.959596 | 0.040404 | 1.000000 | 0.000000 | 1.000000 | 0.000000 | 0.000000 | 0.0 | 0.000000 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 15.10 | 93.0 | 100.0 | 0.0 | NaN | 0.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 309 | 50 | 0.357798 | 0.642202 | 0.132653 | 0.132653 | 0.125000 | 0.173469 | 0.522959 | 0.0 | 0.017857 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 36.82 | 110.0 | 0.0 | 0.0 | 1.27 | 0.0 |
| 310 | 50 | 0.356863 | 0.643137 | 0.163539 | 0.163539 | 0.152815 | 0.214477 | 0.640751 | 0.0 | 0.021448 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 36.72 | 110.0 | 0.0 | 0.0 | 1.33 | 0.0 |
| 311 | 50 | 0.358650 | 0.641350 | 0.146982 | 0.146982 | 0.139108 | 0.194226 | 0.577428 | 0.0 | 0.018373 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 37.03 | 110.0 | 0.0 | 0.0 | 1.38 | 0.0 |
| 312 | 50 | 0.360784 | 0.639216 | 0.163539 | 0.166220 | 0.155496 | 0.214477 | 0.651475 | 0.0 | 0.021448 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 34.83 | 110.0 | 0.0 | 0.0 | 1.24 | 0.0 |
| 313 | 50 | 0.359833 | 0.640167 | 0.152231 | 0.149606 | 0.139108 | 0.196850 | 0.590551 | 0.0 | 0.020997 | ... | 0.0 | 2.0 | 1.0 | 2.0 | 36.53 | 110.0 | 0.0 | 0.0 | 1.42 | 0.0 |
314 rows × 21 columns
D. 建立模型
在决策树中做决策的方法包括基尼系数和信息熵,他们都是衡量数据不确定性或纯度的指标,用于决策树算法中选择最优分裂属性。
- 信息熵是度量数据集不确定性的另一种方法,基于信息论。数据集的信息熵越小,其包含的信息量越少,数据集的纯度越高。信息熵的计算公式是 。
0.9954337899543378
- 基尼系数反映了从数据集中随机选择两个样本,其类别标签不一致的概率。基尼系数越小,数据集的纯度越高。计算公式是 ,其中 是某类别在数据集中的相对频率。
0.8105263157894737
基尼系数和信息熵的主要区别在于计算方法不同,但都旨在衡量数据集的不纯度。在实际应用中,这两种方法没有绝对的优劣之分,选择哪一种主要基于问题本身的需求和数据的特性。
E. 画出一棵树
我们发现,生成的决策树模型比较大,我们不对决策树模型进行解读,先进行剪枝处理,再对最终的决策树模型进行解读。
2.1.2 random_state & splitter
random_state用来设置分枝中的随机模式的参数,默认None,在高维度时随机性会表现更明显,低维度的数据(比如鸢尾花数据集),随机性几乎不会显现。输入任意整数,会一直长出同一棵树,让模型稳定下来。
splitter也是用来控制决策树中的随机选项的,有两种输入值,输入best,决策树在分枝时虽然随机,但是还是会优先选择更重要的特征进行分枝(重要性可以通过属性 feature_importances_ 查看),输入random,决策树在分枝时会更加随机,树会因为含有更多的不必要信息而更深更大,并因这些不必要信息而降低对训练集的拟合。这也是防止过拟合的一种方式。当你预测到你的模型会过拟合,用这两个参数来帮助你降低树建成之后过拟合的可能性。当然,树一旦建成,我们依然是使用剪枝参数来防止过拟合。
0.8105263157894737
上面的训练将会依据我们的训练数据生成一个较大的决策树图,决策树大的好处是能够对数据进行更加细致的划分,但是很可能出现模型过拟合的情况,而对于一些位置数据的划分效果不好,因此,通常我们会对较大的决策树进行剪枝处理。
2.1.3 剪枝参数
在不加限制的情况下,一棵决策树会生长到衡量不纯度的指标最优,或者没有更多的特征可用为止。这样的决策树往往会过拟合,这就是说, 它会在训练集上表现很好,在测试集上却表现糟糕。 我们收集的样本数据不可能和整体的状况完全一致,因此当一棵决策树对训练数据有了过于优秀的解释性,它找出的规则必然包含了训练样本中的噪声,并使它对未知数据的拟合程度不足。
为了让决策树有更好的泛化性,我们要对决策树进行剪枝。 剪枝策略对决策树的影响巨大,正确的剪枝策略是优化决策树算法的核心。 sklearn为我们提供了不同的剪枝策略:
0.9954337899543378
max_depth
一般
max_depth用作树的”精修“限制树的最大深度,超过设定深度的树枝全部剪掉
这是用得最广泛的剪枝参数,在高维度低样本量时非常有效。决策树多生长一层,对样本量的需求会增加一倍,所以限制树深度能够有效地限制过拟合。在集成算法中也非常实用。实际使用时,建议从 开始尝试,看看拟合的效果再决定是否增加设定深度。
min_samples_leaf & min_samples_split
min_samples_leaf限定一个节点在分枝后的每个子节点都必须包含至少min_samples_leaf个训练样本,否则分枝就不会发生,或者,分枝会朝着满足每个子节点都包含min_samples_leaf个样本的方向去发生一般搭配
max_depth使用,在回归树中有神奇的效果,可以让模型变得更加平滑。这个参数的数量设置得太小会引起过拟合,设置得太大就会阻止模型学习数据。一般来说,建议从 开始使用。如果叶节点中含有的样本量变化很大,建议输入浮点数作为样本量的百分比来使用。同时,这个参数可以保证每个叶子的最小尺寸,可以在回归问题中避免低方差,过拟合的叶子节点出现。对于类别不多的分类问题, 通常就是最佳选择。min_samples_split限定一个节点必须要包含至少min_samples_split个训练样本,这个节点才允许被分枝,否则分枝就不会发生。
- max_features & min_impurity_decrease
max_features限制分枝时考虑的特征个数,超过限制个数的特征都会被舍弃。和max_depth异曲同工,max_features是用来限制高维度数据的过拟合的剪枝参数,但其方法比较暴力,是直接限制可以使用的特征数量而强行使决策树停下的参数,在不知道决策树中的各个特征的重要性的情况下,强行设定这个参数可能会导致模型学习不足。如果希望通过降维的方式防止过拟合,建议使用 , 或者特征选择模块中的降维算法。min_impurity_decrease限制信息增益的大小,信息增益小于设定数值的分枝不会发生。这是在sklearn 0.19版本种更新的功能,在0.19版本之前时使用min_impurity_split。
The score after pruning is 0.8210526315789474
决策树解读
- 根节点信息解读:

Ti <= 0.685:这是决策树在当前节点上做出决策的条件。意味着如果某个样本在“Ti”这个特征上的值小于或等于0.685,那么它会被分到左侧的子节点;否则,它会被分到右侧的子节点。这里的“Ti”代表某个具体的特征,可能是材料的成分比例、温度、压力等任何一个能影响到最终分类的因素。gini = 0.25:基尼不纯度(Gini impurity),是一种衡量数据集混杂程度的指标,范围从0到1。值越低表示数据集越“纯”,即在当前节点下的样本属于同一个类别的概率越高。这里的0.25表示在当前节点下,数据集有一定的混杂度。samples = 219:这表示当前节点包含的样本总数。也就是说,在分到这个节点的样本有219个。value = [187, 32]:这代表当前节点包含的样本中,各个类别的数量。假设我们的目标是预测材料是否具有某种特性(比如是不是热导材料),这里的数组表示在这219个样本中,有187个属于第一类(比如不是热导材料),32个属于第二类(比如是热导材料)。class = Heat:这表示如果当前节点是一个叶子节点(即没有进一步的分支),那么它会将样本分类到“Heat”这个类别。在多数情况下,叶子节点会选择最多数的类别作为该节点的类别。
- 子节点信息解读

子节点的显示信息可解读为:
gini=0.0:这是基尼不纯度,一个衡量标准,用于评估分割的质量。基尼不纯度表示在这个节点上的数据混合度。值为0意味着这个节点是完全纯净的,也就是说,所有的样本都属于同一个类。在这个案例中,所有的61个样本都被正确地分类到了同一个类别,没有混杂其他类别的样本。
samples=61:这表示在当前节点包含的样本数量,这里有61个样本。
value=[61,0]:这个数组展示了每个类别的样本数量。在二分类问题中,这个数组有两个值。第一个值(61)表示第一个类别的样本数量,第二个值(0)表示第二个类别的样本数量。这个子节点的所有样本都被分类到第一个类别,没有样本被分类到第二个类别。
class = Heat:这指的是当前节点样本的主要(或纯净的)类别。由于这个节点是完全纯净的(gini=0),所以这里的所有样本都被归类为“heat”。
总的来说,这个子节点是一个完全纯净的节点,它的所有个样本都被准确分类为“Heat”类别,没有任何误分类。这样的节点在决策树中是理想的末端节点(叶节点),因为它们不需要进一步的分割来区分样本。
确认最优的剪枝参数
怎么来确定每个参数的值呢?这时候,我们就要使用确定超参数的曲线来进行判断了,继续使用我们已经训练好的决策树模型 clf。超参数的学习曲线,是一条以超参数的取值为横坐标,模型的度量指标为纵坐标的曲线,它是用来衡量不同超参数取值下模型的表现的线。在我们建好的决策树里,我们的模型度量指标就是 score。
- 思考:
- 剪枝参数一定能够提升模型在测试集上的表现吗? - 调参没有绝对的答案,一切都是看数据本身。
- 这么多参数,一个个画学习曲线?
剪枝参数的默认值会让树无尽地生长,这些树在某些数据集上可能非常巨大,对内存消耗很大。所以如果你手中的数据集非常大,通常都要进行剪枝处理,因此提前设定这些参数来控制树的复杂性和大小会比较好。
2.1.4 目标权重参数
- class_weight & min_weight_fraction_leaf
完成样本标签平衡的参数。样本不平衡是指在一组数据集中,标签的一类天生占有很大的比例。比如说,在银行要判断“一个办了信用卡的人是否会违约”,就是是vs否(1%:99%)的比例。这种分类状况下,即便模型什么也不做,全把结果预测成“否”,正确率也能有99%。因此我们要使用class_weight参数对样本标签进行一定的均衡,给少量的标签更多的权重,让模型更偏向少数类,向捕获少数类的方向建模。该参数默认None,此模式表示自动给与数据集中的所有标签相同的权重。
有了权重之后,样本量就不再是单纯地记录数目,而是受输入的权重影响了,因此这时候剪枝,就需要搭配min_ weight_fraction_leaf这个基于权重的剪枝参数来使用。另请注意,基于权重的剪枝参数(例如min_weight_ fraction_leaf)将比不知道样本权重的标准(比如min_samples_leaf)更少偏向主导类。如果样本是加权的,则使用基于权重的预修剪标准来更容易优化树结构,这确保叶节点至少包含样本权重的总和的一小部分。
2.2 重要属性和接口
属性是在模型训练之后,能够调用查看的模型的各种性质。对决策树来说,最重要的是 feature_importances_,能够查看各个特征对模型的重要性。
sklearn中许多算法的接口都是相似的,比如说我们之前已经用到的 fit 和 score,几乎对每个算法都可以使用。除了这两个接口之外,决策树最常用的接口还有 apply 和 predict。apply 中输入测试集返回每个测试样本所在的叶子节点的索引,predict输入测试集返回每个测试样本的标签。返回的内容一目了然并且非常容易,大家自己下去试试看。
array([0.14292216, 0.16433898, 0.0121381 , 0.14565721, 0. ,
0.14565721, 0.08459588, 0.07192949, 0. , 0. ,
0. , 0.23276096, 0. , 0. , 0. ])| Importance | |
|---|---|
| Y | 0.232761 |
| Ti | 0.164339 |
| Cr | 0.145657 |
| Mn | 0.145657 |
| Journal | 0.142922 |
| V | 0.084596 |
| Ni | 0.071929 |
| Zr | 0.012138 |
| Co | 0.000000 |
| Sn | 0.000000 |
| Al | 0.000000 |
| Fe | 0.000000 |
| B | 0.000000 |
| A | 0.000000 |
| B/A | 0.000000 |
结果中 B 为 AB2 合金中 B 的比例,A 为 AB2 合金中 A 的比例,一般皆为 1:2
Journal 表现出较为靠前的重要性,表明对于实验数据,不同的文献来源可能会引起较大的偏差。
array([ 6, 9, 9, 9, 9, 22, 22, 22, 9, 10, 6, 10, 22, 9, 9, 22, 22,
9, 6, 9, 9, 6, 9, 22, 9, 22, 9, 6, 6, 22, 10, 9, 22, 9,
22, 18, 22, 6, 9, 18, 9, 9, 22, 10, 9, 6, 22, 9, 10, 22, 22,
22, 14, 9, 6, 6, 9, 9, 9, 22, 22, 7, 22, 6, 7, 9, 9, 9,
6, 22, 9, 10, 22, 9, 10, 9, 9, 17, 10, 9, 9, 20, 9, 9, 7,
9, 6, 6, 9, 10, 9, 17, 22, 7, 22])array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])至此,我们已经学完了分类树 DecisionTreeClassifier 和用决策树绘图的所有基础。我们讲解了决策树的基本流程,分类树的七个参数,一个属性,四个接口,以及绘图所用的代码。
- 七个参数:criterion,两个随机性相关的参数(random_state,splitter),四个剪枝参数(max_depth, ,min_sample_leaf,max_feature,min_impurity_decrease)
- 一个属性:feature_importances_
- 四个接口:fit,score,apply,predict
有了这些知识,基本上分类树的使用大家都能够掌握了,接下来再到实例中去磨练就好。
3 回归树算法(DecisionTreeRegressor)
在Scikit-learn中,回归树(DecisionTreeRegressor)主要用于处理回归问题,即目标变量(或称为标签)是连续性的数值。回归树通过将特征空间划分成不同的区域,并在每个区域内对目标变量的值进行预测,来解决回归问题。使用回归树的步骤包括实例化模型、训练模型与数据拟合、以及使用训练好的模型进行预测。
它可以通过DecisionTreeRegressor类在Scikit-learn中实现,该类提供了许多参数(如max_depth, min_samples_split等)来调整树的结构和解决过拟合或欠拟合的问题。
实例
回归树可视化选择 吸氢金属合金材料的 曲线的实验数据进行展示。
() 曲线是一定温度下合金中氢浓度与氢吸收/解吸压力曲线,是在特定应用下选择吸氢材料的重要参考。
sklearn 中的回归树:
classsklearn.tree.DecisionTreeRegressor(criterion=’mse’, splitter=’best’, max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, presort=False)
3.1 重要参数
回归树衡量分枝质量的指标,支持的标准有三种:
1)输入 "squared_error" 使用均方误差 mean squared error(MSE),父节点和叶子节点之间的均方误差的差额作为特征选择的标准,这种方法通过使用叶子节点的均值来最小化 损失
2)输入 "friedman_mse" 使用费尔德曼均方误差,这种指标使用弗尔德曼针对潜在分枝中的问题改进后的均方误差
3)输入 "absolute_error" 使用绝对平均误差 (meanabsoluteerror),这种指标使用叶节点的中值来最小化 损失
属性中最重要的依然是 feature_importances_,接口依然是apply, fit, predict, score最核心。
- 数据集介绍
PCT曲线中包含如下几列:
Vacuometer1(Pm(Pa))
- 解释:金属氢化物吸附氢气的平衡压力(Pm),单位为帕斯卡(Pa)。
- 背景:平衡压力是描述氢在金属氢化物中的吸附和解吸过程中的一个关键参数。它反映了金属氢化物与氢气之间的相互作用力。
Vacuometer1(Pg(Pa))
- 解释:金属氢化物脱附氢气的平衡压力(Pg),单位同样为帕斯卡(Pa)。一般吸附氢气的压力高于脱附氢气的压力。
Velocity
- 解释:这里的 Velocity 是指氢气在样品中的传输速度。
- 背景:传输速度是评价氢在金属氢化物中扩散效率的一个指标。较高的传输速度意味着氢气能够迅速进入或离开金属氢化物,这对于快速储氢和释放氢气具有重要意义。
Capacity
- 解释:表示氢气在样品中的存储容量。
- 背景:储氢容量是衡量金属氢化物储氢能力的一个重要参数。较高的储氢容量表明金属氢化物能够在单位体积或质量下存储更多的氢气,是评价储氢材料性能的重要指标。
Velocity(L/s)
- 样品中氢气流动的速度,数值与Velocity列一样,单位换算为升每秒(L/s)。
Capacity(Pa·L)
- 解释:样品的氢存储容量,数值与Capacity列一样,单位换为帕斯卡·升(Pa·L)。
这些数据列分别代表了 PCT 曲线中的重要参数,它们共同描述了金属氢化物在不同压力条件下的氢吸附和解吸行为。理解这些参数对于研究和开发高效储氢材料具有重要意义。
3.1.1 读取数据
| Vacuometer1(Pm(Pa)) | Vacuometer1(Pg(Pa)) | Velocity | Capacity | Velocity(L/s) | Capacity(Pa·L) | |
|---|---|---|---|---|---|---|
| 0 | 0.09032 | 0.000371 | 25582.66086 | 9.503959 | 25.582661 | 0.009504 |
| 1 | 0.09035 | 0.000374 | 25426.24960 | 19.010833 | 25.426250 | 0.019011 |
| 2 | 0.09068 | 0.000372 | 25636.54527 | 28.552755 | 25.636545 | 0.028553 |
| 3 | 0.09059 | 0.000376 | 25384.99087 | 38.084819 | 25.384991 | 0.038085 |
| 4 | 0.09086 | 0.000376 | 25433.75899 | 47.645369 | 25.433759 | 0.047645 |
| ... | ... | ... | ... | ... | ... | ... |
| 10055 | 0.05535 | 0.000381 | 15256.25489 | 68838.308140 | 15.256255 | 68.838308 |
| 10056 | 0.05517 | 0.000380 | 15218.37312 | 68844.097210 | 15.218373 | 68.844097 |
| 10057 | 0.05522 | 0.000381 | 15220.17452 | 68849.891530 | 15.220175 | 68.849892 |
| 10058 | 0.05504 | 0.000384 | 15023.18079 | 68855.666440 | 15.023181 | 68.855666 |
| 10059 | 0.05517 | 0.000382 | 15142.21392 | 68861.455300 | 15.142214 | 68.861455 |
10060 rows × 6 columns
3.1.2 划分特征与标签
0.9355869551372221
3.1.3 训练并绘制决策树模型
3.2 交叉验证/剪枝参数优化
通过交叉验证(cross_val_score)评估不同深度下模型的性能,并记录每次的交叉验证得分。然后,通过绘制交叉验证得分的曲线,可以直观地观察不同剪枝程度对模型性能的影响。
[<matplotlib.lines.Line2D at 0x7f4155a8e5e0>]
3.3 回归树可视化
选择数据中的前600个数据进行回归树模型训练与模型性能评估
/tmp/ipykernel_100/645056539.py:2: FutureWarning: Support for multi-dimensional indexing (e.g. `obj[:, None]`) is deprecated and will be removed in a future version. Convert to a numpy array before indexing instead. X_100 = df_PCT['Velocity'][:num][:, np.newaxis]
3.3.1 最大深度为2
<matplotlib.legend.Legend at 0x7f4155370670>
| Xtest | Ytest | Ypred | |
|---|---|---|---|
| 1 | 25426.24960 | 19.010833 | 666.245506 |
| 8 | 25283.90650 | 85.932929 | 666.245506 |
| 14 | 24843.96242 | 143.621768 | 666.245506 |
| 17 | 24794.08202 | 172.566575 | 666.245506 |
| 21 | 24655.12166 | 211.228625 | 666.245506 |
| 48 | 23555.17549 | 474.293022 | 666.245506 |
| 52 | 23711.91823 | 513.186785 | 666.245506 |
| 85 | 22747.34659 | 824.117528 | 666.245506 |
| 92 | 22619.95106 | 889.485376 | 666.245506 |
| 103 | 22537.96464 | 992.142804 | 666.245506 |
| 122 | 22665.84824 | 1169.896207 | 666.245506 |
| 127 | 22289.33125 | 1216.245403 | 666.245506 |
| 162 | 21910.12790 | 1528.816623 | 2024.322557 |
| 173 | 22143.71905 | 1625.964738 | 2024.322557 |
| 181 | 22133.95921 | 1696.653750 | 2024.322557 |
| 186 | 22064.54149 | 1740.905574 | 2024.322557 |
| 187 | 22001.46090 | 1749.750161 | 2024.322557 |
| 190 | 22033.00119 | 1776.344266 | 2024.322557 |
| 194 | 22020.10661 | 1811.742680 | 2024.322557 |
| 200 | 21948.43498 | 1864.754816 | 2024.322557 |
| 205 | 21968.28040 | 1908.963732 | 2024.322557 |
| 224 | 21922.11888 | 2076.944842 | 2024.322557 |
| 231 | 21752.78505 | 2138.857534 | 2024.322557 |
| 239 | 21987.84075 | 2209.565322 | 2024.322557 |
| 245 | 21810.16789 | 2262.517106 | 2024.322557 |
| 266 | 21819.70041 | 2448.298693 | 2024.322557 |
| 283 | 21823.52899 | 2598.890027 | 2024.322557 |
| 299 | 21578.23749 | 2740.449449 | 3253.974562 |
| 312 | 21636.61313 | 2855.472161 | 3253.974562 |
| 315 | 21662.31651 | 2882.044985 | 3253.974562 |
| 320 | 21625.38985 | 2926.293999 | 3253.974562 |
| 333 | 21611.62111 | 3041.391096 | 3253.974562 |
| 343 | 21531.69286 | 3129.772072 | 3253.974562 |
| 346 | 21482.94306 | 3156.287248 | 3253.974562 |
| 348 | 21751.17747 | 3173.972957 | 2024.322557 |
| 354 | 21559.40410 | 3227.028753 | 3253.974562 |
| 355 | 21836.51252 | 3235.914030 | 2024.322557 |
| 365 | 21493.77121 | 3324.263392 | 3253.974562 |
| 366 | 21501.82285 | 3333.102792 | 3253.974562 |
| 384 | 21559.79415 | 3492.100467 | 3253.974562 |
| 400 | 21395.18945 | 3633.389209 | 3253.974562 |
| 427 | 21031.58628 | 3868.502647 | 4569.413882 |
| 432 | 21076.19200 | 3910.967644 | 4569.413882 |
| 434 | 20987.14861 | 3927.905280 | 4569.413882 |
| 439 | 21208.51241 | 3970.370933 | 4569.413882 |
| 446 | 21113.14060 | 4029.700459 | 4569.413882 |
| 457 | 21184.86963 | 4122.958215 | 4569.413882 |
| 477 | 21200.72260 | 4292.510860 | 4569.413882 |
| 479 | 21110.46839 | 4309.488784 | 4569.413882 |
| 480 | 21200.72260 | 4317.966953 | 4569.413882 |
| 482 | 21152.59541 | 4334.938738 | 4569.413882 |
| 484 | 21086.80728 | 4351.891505 | 4569.413882 |
| 495 | 21063.11872 | 4445.091676 | 4569.413882 |
| 499 | 21063.11872 | 4478.970657 | 4569.413882 |
| 524 | 20989.58870 | 4690.535281 | 4569.413882 |
| 525 | 21049.97171 | 4699.005790 | 4569.413882 |
| 526 | 21060.46621 | 4707.482628 | 4569.413882 |
| 569 | 20869.02983 | 5070.599500 | 4569.413882 |
| 580 | 20903.23588 | 5163.318633 | 4569.413882 |
| 594 | 20856.21615 | 5281.268233 | 4569.413882 |
3.3.2 最大深度为5
<matplotlib.legend.Legend at 0x7f4155095f40>
3.3.3 最大深度为10
[<matplotlib.lines.Line2D at 0x7f4155624670>]
可以看到,当设置剪枝参数 max_depth=2 时,学习程度不足,而当设置剪枝参数 max_depth=10 时,模型学习到了许多噪音,出现了过拟合。而当剪枝参数 max_depth=5 时,模型学习的比较合适。
到目前为止,我们就得到了一个模型效果还行的决策树模型。
随堂作业
吸氢金属通常指的是能够在其金属结构中吸收并储存氢气的材料,这类材料在能源存储、传感器和催化剂等领域具有重要应用。请使用以下数据集 hydrogen_metal_data_300.csv,用决策树算法判断材料是否为吸氢金属:
数据集介绍
数据集中提供了四个特征,用以判断一个材料是否可作为有效的吸氢金属:
- 吸氢容量大小:高/低(一个材料吸收氢气的能力,高吸氢容量表明材料能够储存更多的氢气)
- 吸放氢平衡压:高/低(吸氢和放氢时所需的压力,低平衡压有利于在较低的外界压力下吸放氢)
- 使用温度:高/低(材料正常工作的温度范围,低温度使用对设备要求较低,更易实现)
- 循环寿命:长/短(材料能够进行吸放氢反应的次数,长寿命表示材料可重复使用多次)
特征数据介绍
为了简化问题,我们可以将吸氢容量大小、吸放氢平衡压、使用温度和循环寿命的特征分别编码为 和 ,其中 代表低/短, 代表高/长。接下来,我们会生成这样的数据集,并用决策树算法(如 、 或 )来训练模型,最后绘制出决策树。
数据集中包含 组数据。每一行代表一个材料,列包括了我们关心的四个特征:吸氢容量大小、吸放氢平衡压、使用温度和循环寿命,以及这些特征组合下的材料是否为吸氢金属( 表示是吸氢金属, 表示不是)。
作业要求
读取数据集并预览
划分数据集为测试集和训练集
提示:获取列标签并转换为列表可使用:
df.columns.tolist()使用sklearn中的决策树算法
DecisionTreeClassifier对训练集构建决策树模型进行剪枝操作 (最大深度设置为 )
使用训练的决策树模型对测试集数据进行模型性能评估
可选: 准确率(accuracy_score), 精确度(precision_score), 召回率(recall_score), F1分数(f1_score), 混淆矩阵(confusion_matrix)
画出特征重要性条形图
| Hydrogen Capacity | Equilibrium Pressure | Operating Temperature | Cycle Life | Is Hydrogen Metal | |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 |
| 2 | 0 | 1 | 0 | 0 | 1 |
| 3 | 0 | 0 | 1 | 0 | 1 |
| 4 | 1 | 1 | 1 | 0 | 0 |
| ... | ... | ... | ... | ... | ... |
| 295 | 1 | 1 | 1 | 1 | 0 |
| 296 | 1 | 1 | 1 | 0 | 0 |
| 297 | 0 | 1 | 0 | 0 | 1 |
| 298 | 0 | 1 | 1 | 0 | 0 |
| 299 | 1 | 0 | 0 | 0 | 1 |
300 rows × 5 columns
0.8208333333333333
The score after pruning is 0.8208333333333333
模型测试结果: 准确率: 0.85 精确度: 0.84375 召回率: 0.8709677419354839 F1 SCORE: 0.8571428571428571 混淆矩阵: [[24 5] [ 4 27]]






