



文献案例|支持向量机(SVM)材料科学实践
1 教学案例|可视化演示、核函数、模型实现、参数优化
1.1 线性支持向量机分类在低维空间中的可视化演示
使用生物炭数据集 [2],数据集详情请见 3.2 小节。该数据集已经过处理以满足教学需要。
1.1.1 导入数据集,预处理并可视化
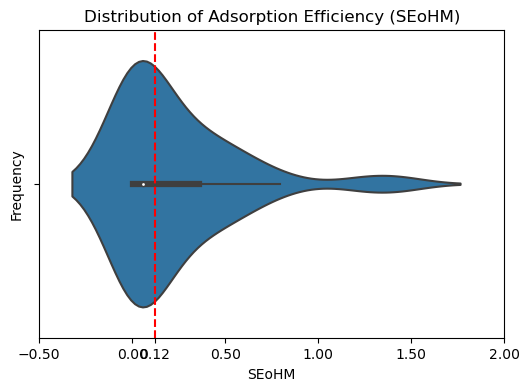
固体生物炭材料中的重金属吸附效率 SEoHM 根据以下方程计算:
其中 是金属的初始浓度(), 是金属的平衡浓度(), 是溶液体积(), 是固体材料质量()。
在这里,我们认为当 SEoHM > 0.12 (数据)时,吸附效果合格。
1.1.2 画决策边界
使用 matplotlib.axes.Axes.coutour([X, Y], Z, [levels], **kwargs) 函数绘制决策边界。
contour 函数是我们专门用来绘制等高线的函数。等高线,本质上是在二维图像上表现三维图像的一种形式,其中两维 X 和 Y 是两条坐标轴上的取值,而Z表示高度。Contour 就是将由 X 和 y 构成平面上的所有点中,高度一致的点连接成线段的函数,在同一条等高线上的点一定具有相同的 Z 值。我们可以利用这个性质来绘制我们的決策边界。
要明白绘制决策边界的意义,首先要理解 contour 函数:
| 参数 | 含义 |
|---|---|
| X, Y | 选填。两维平面上所有的点的横纵坐标取值,一般要求是二维结构并且形状需要与 Z 相同,往往通过 numpy.meshgrid() 这样的函数来创建。如果 X 和 Y 都是一维,则 Z 的结构必须为(len(Y),len(X)。如果不填写,则默认 X=range(Z.shape[1)), Y=range(Z.shaper[O])。 |
| Z | 必填。平面上所有的点所对应的高度。 |
| levels | 可不填,不填默认显示所有的等高线,填写用于确定等高线的数量和位置。如果填写整数 n,则显示 n 个数据区间,即绘制 n+1 条等高线。水平高度自动选择。如果填写的是数组或列表,则在指定的高度级别绘制等高线。列表或数组中的值必须按递增顺序排列。 |
使用 np.meshgrid 函数建立 coutour 函数所需的网格

我们的决策边界是
在决策边界的两边找出两个超平面,使得超平面到决策边界的相对距离为1。我们只需要在我们的样本构成的平面上,把所有到决策边界的距离为 0 的点相连,就是我们的决策边界,而把所有到决策边界的相对距离为 1 的点相连,就是我们的两个平行于决策边界的支持向量了。此时,我们的 Z 就是平面上的任意点到达决策边界的距离。
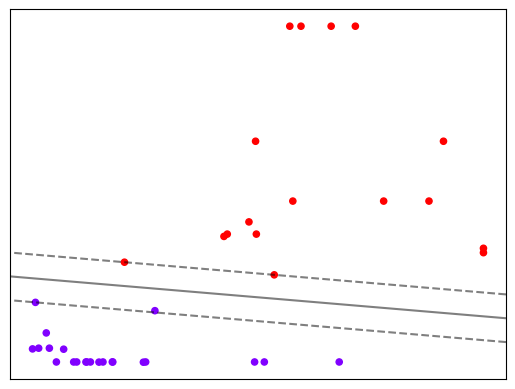
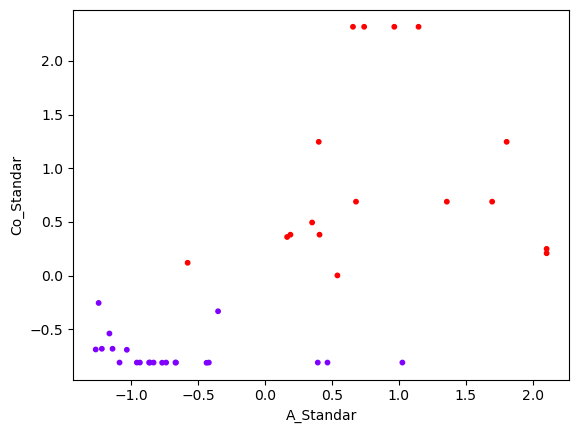
从这个图里可以简单判断,环境金属含量 Co 与灰分百分比 A 都与吸附效率呈正相关,且环境金属含量 Co 起显著的主要影响。
1.1.3 维度变换
当我们使用不同的特征来查看数据:
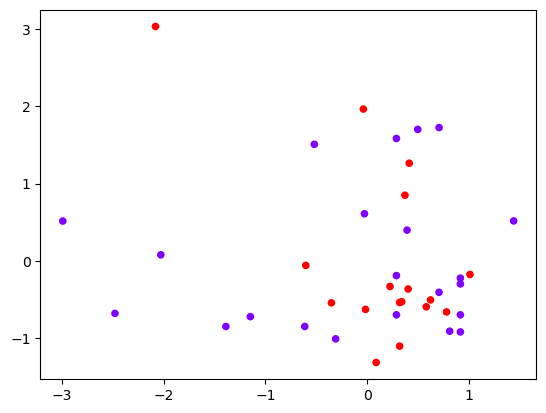
让我们再试一下刚才绘制线性决策边界的方式,看看是否能够再划分数据。
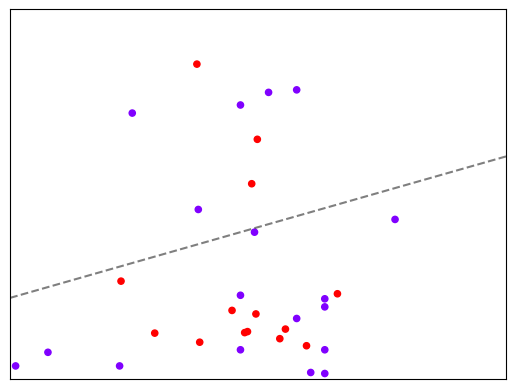
明显,现在线性 SVM 已经不适合于我们的状况了,我们无法找出一条直线来划分我们的数据集,让直线的两边分别是两种类别。
这个时候,如果我们能够在原本的 X 和 y 的基础上,添加一个维度 h,变成三维,我们可视化这个数据,来看看添加维度让我们的数据如何变化。
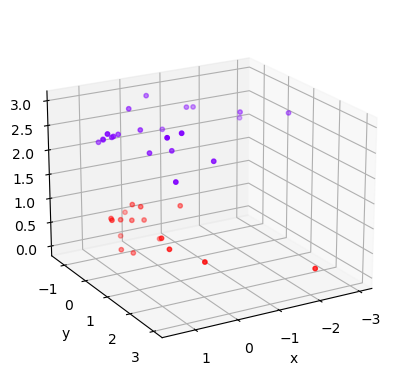
此时我们的数据在三维空间中,我们的超平面就是一个二维平面。明显我们可以用一个平面将两个数据集分开,这个平面就是我们的超平面。 我们刚才计算 h,并将 h 作为数据的第三维度来将数据升维的过程,被称为"核变换”,即是将数据投影到高维空间中,以寻找能够将数据完美分割的超平面。为了详细解释这个过程,我们需要引入 SVM 中的核心概念:核函数。
1.2 核函数
"核技巧"(Kernel Trick),是一种能够使用数据原始空间中的向量计算来表示升维后的空间中的点积结果的数学方式。具体表现为 而这个原始空间中的点积函数 ,就被叫做'核函数"(Kernel Function)。
核函数的意义:
- 有了核函数之后,我们无需去担心 究竟应该是什么样,因为非线性 SVM 中的核核函数都是正定核函数 (positive definite kernel functions),他们都满足美世定律(Mercer's theorem),确保了高维空问中任意两个向量 的点积一定可以被低维空问中的这两个向量的某种计算来表示(多数时候是点积的某种变换)。
- 使用核函数计算低维度中的向量关系可大大简化计算
- 计算是在原始空间中进行,所以避免了维度灾难的问题
参数 kernel 在 sklearn 中的几个选项:
| 输入 | 含义 | 解决问题 | 核函数的表达式 | 参数 gamma | 参数 degree | 参数 coef0 |
|---|---|---|---|---|---|---|
| “linear” | 线性核 | 线性 | No | No | No | |
| ”poly” | 多项式核 | 偏线性 | Yes | Yes | Yes | |
| “sigmoid” | 双曲正切核 | 非线性 | Yes | No | Yes | |
| “rbf” | 高斯径向基 | 偏非线性 | Yes | No | No |
1.2.1 查看不同核函数的区别
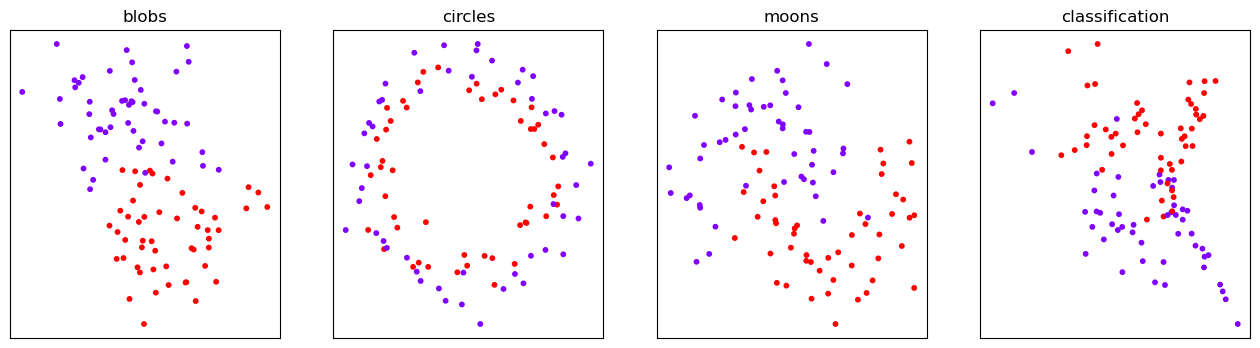
同样的,我们使用上一小节中的等高线画法,来绘制一个不同核函数的分类效果。

可以观察到,线性核函数和多项式核函数在非线性数据上表现会浮动,如果数据相对线性可分,则表现不错,如果是像环形数据那样彻底不可分的,则表现糟糕。在线性数据集上,线性核函数和多项式核函数即便有扰动项也可以表现不错,可见多项式核函数是虽然也可以处理非线性情况,但更偏向于线性的功能。
sigmoid核函数就比较尴尬了,它在非线性数据上强于两个线性核函数,但效果明显不如 rbt,它在线性数据上完全比不上线性的核函数们,对扰动项的抵抗也比较弱,所以它功能比较弱小,很少被用到。
rbf,高斯径向基核函数基本在任何数据集上都表现不错,属于比较万能的核函数。无论如何先试试看高斯径向基核函数,它适用于核转换到很高的空间的情况,在各种情况下往往效果都很不错,如果 rbf 效果不好,那我们再试试看其他的核函数。另外,多项式核函数多被用于图像处理之中。
1.3 模型实现|SVM 预测高熵合金相态(分类)
本案例与「第 2 节」中实践案例相同,经过简化供教学示范使用。
1.3.1 案例背景
高熵合金(HEAs)是一类独特的多主元素合金(MPEAs),可以作为单相固溶体结晶。自 2004 年被提出以来,HEAs 引起了广泛的关注,不仅因为其优越的性能,还因为它为合金设计开辟了一个广阔的新领域。到目前为止,MPEAs 的组成空间中极小的部分已经通过试错方法进行了研究,周期表中有 80 多种金属元素,有效识别 MPEAs 的相位并找到所有可能的 HEA 组成是一个巨大的挑战。目前,研究人员使用高配位熵、混合焓、原子尺寸差等参数来识别HEAs,但这些参数并不稳健。热力学计算方法(如CALPHAD)和第一性原理计算在计算相稳定性方面更有效,但受限于计算成本和数据范围。机器学习(ML)在从现有数据中提取隐含关系方面表现出优势。支持向量机(SVM)是另一种著名的 ML 算法,它需要较少的训练样本,并具有许多内在优点,包括良好的理论基础、凸性、优秀的泛化能力和高计算速度。因此,这项研究采用了机器学习方法,构建了一个支持向量机(SVM)模型,将该模型应用于 16 个元素的组成空间,预测了多种高熵合金的相态。[2.2]
1.3.2 数据集介绍
在这里,我们选择参考文献 [2.3] 中的数据集,该数据集收集了 408 个经实验合成的 MPEA 样品,包含 648 个微观结构表征。我们只考虑最常见的铸态样品,以排除加工条件和热力学处理的影响。排除含有稀土元素或轻元素(除 Al 外)的样品以及相不确定的样品,以降低复杂性。不考虑密堆积六方 HEA,因为它们通常包含稀土元素。
然后,我们得到了一个包含 322 个不同铸态 MPEA 样品的数据集,其中包含 3-9 个组分元素。其中,有 18 个样品具有单个 BCC 相,43 个样品具有单个 FCC 相。其余的 261 个样品具有多相、金属间化合物或非晶相,用“NSP”标记,表示“不形成单相固溶体”。三元到九元 MPEA 的百分比以及 BCC、FCC 和 NSP 相的比例如图 (a) 所示。大多数样品由五个或六个元素组成,而单相 HEA 仅占很小一部分。数据集中有 18 个元素(Al、Ti、V、Cr、Mn、Fe、Co、Ni、Cu、Y、Zr、Nb、Mo、Ag、Hf、Ta、W 和 Au),它们的出现次数如图 (b) 所示。我们发现 Fe、Ni、Cr、Co 和 Al 在 200 个以上的样品中出现,而 Hf、Ag 和 Au 仅出现一次。

特征构建|MPEAs的热力学参数被用作候选特征,可以通过以下方程计算:
其中,、、、 和 分别表示第 i 个元素的摩尔分数、原子半径、熔点、价电子浓度和 Pauling 电负性。N 是组成元素的数量,R 是气体常数。 是二元液态合金的混合焓,来源于 Miedema's 理论 [3]。
最稳定的二元化合物的形成焓 可以从参考文献 [4] 中得出,也被认为是候选特征。
1.3.3 代码实现
| Alloy | VEC | Tm | HIM | rd | ΔH | SC | χd | Ref. | Phase | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | HfNbTiZr | 4.25 | 2331.25 | -22 | 0.05 | 3.59 | 1.39 | 0.09 | [S1] | BCC |
| 1 | MoNbTaW | 5.50 | 3157.75 | -193 | 0.02 | -9.90 | 1.39 | 0.19 | [S2] | BCC |
| 2 | NbTaTiV | 4.75 | 2541.00 | -122 | 0.04 | -0.11 | 1.39 | 0.03 | [S3] | BCC |
| 3 | Al0.25NbTaTiV | 4.65 | 2446.41 | -428 | 0.04 | -10.75 | 1.53 | 0.03 | [S3] | BCC |
| 4 | Al0.5NbTaTiV | 4.56 | 2362.33 | -428 | 0.04 | -19.08 | 1.58 | 0.03 | [S3] | BCC |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 317 | CoCrCuFeMnNiTiV | 7.50 | 1811.00 | -435 | 0.05 | -12.11 | 2.08 | 0.09 | [S10] | NSP |
| 318 | Al0.125CoCrCuFeMnNiTiV | 7.43 | 1797.49 | -677 | 0.06 | -14.12 | 2.13 | 0.09 | [S10] | NSP |
| 319 | Al0.125CoCrCuFeNiTiMnV | 7.43 | 1797.49 | -677 | 0.06 | -14.12 | 2.13 | 0.09 | [S10] | NSP |
| 320 | Al0.67CoCrCuFeMnNiTiV | 7.15 | 1743.15 | -677 | 0.06 | -21.53 | 2.19 | 0.08 | [S10] | NSP |
| 321 | Al0.67CoCrCuFeNiTiMnV | 7.15 | 1743.15 | -677 | 0.06 | -21.53 | 2.19 | 0.08 | [S10] | NSP |
322 rows × 10 columns
The average accuracy under kernel linear is 0.8062310949788264 00:19:889425 The average accuracy under kernel rbf is 0.8131276467029643 00:00:062660 The average accuracy under kernel poly is 0.8304900181488204 02:21:674404 The average accuracy under kernel sigmoid is 0.8062310949788264 00:00:026650

可以看到多项式核占用了大部分的计算时间,但是为什么 rbf 核效果还略差呢?
其实,这里真正的问题是数据的量纲问题。回忆一下我们如何求解决策边界,如何判断点是否在决策边界的一边?是靠计算-距离”,虽然我们不能说SVM是完全的距离类模型,但是它严重受到数据量纲的影响。让我们来探索一下数据集的量纲:
| count | mean | std | min | 1% | 5% | 50% | 95% | 99% | max | |
|---|---|---|---|---|---|---|---|---|---|---|
| VEC | 322.0 | 7.329907 | 0.902012 | 3.80 | 4.5789 | 5.5065 | 7.500 | 8.4285 | 8.7937 | 9.50 |
| Tm | 322.0 | 1766.319006 | 205.083744 | 1339.67 | 1458.3140 | 1533.8645 | 1739.475 | 2048.0805 | 2442.7014 | 3157.75 |
| HIM | 322.0 | -628.745342 | 384.504808 | -2505.00 | -2505.0000 | -677.0000 | -677.000 | -115.0000 | -97.0000 | -22.00 |
| rd | 322.0 | 0.054658 | 0.018896 | 0.00 | 0.0121 | 0.0300 | 0.050 | 0.0900 | 0.1079 | 0.14 |
| ΔH | 322.0 | -18.375031 | 10.706515 | -49.15 | -43.8022 | -34.9025 | -18.255 | -0.7630 | 6.1829 | 7.66 |
| SC | 322.0 | 1.678820 | 0.169074 | 1.10 | 1.1963 | 1.3900 | 1.680 | 1.9300 | 2.1458 | 2.19 |
| χd | 322.0 | 0.079752 | 0.024018 | 0.02 | 0.0300 | 0.0600 | 0.070 | 0.1300 | 0.1779 | 0.19 |
- 从上表各特征的平均值(mean 列) 可以看出量纲不统一;
- 从最小值、最大值分别与1%数据,99%数据比较看出无明显偏布;(为什么要在标准化前查看数据有无偏布?)
因此我们对训练集进行标准化处理后重新建立模型;
The average accuracy under kernel linear is 0.8408348457350272 00:00:021493 The average accuracy under kernel rbf is 0.8513611615245008 00:00:020910 The average accuracy under kernel poly is 0.8270417422867513 00:00:019253 The average accuracy under kernel sigmoid is 0.7958862673926195 00:00:023404
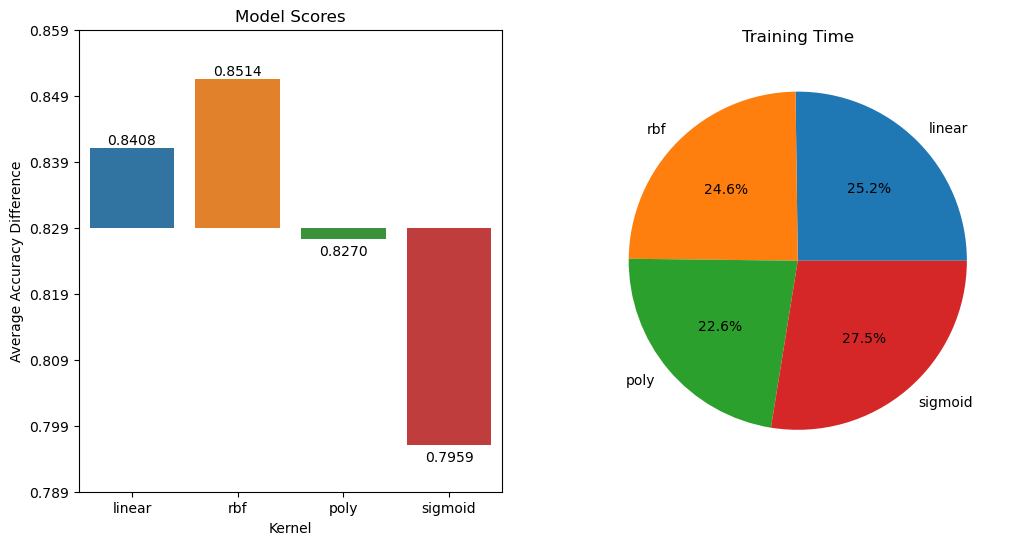
量纲统一之后,可以观察到,所有核函数的运算时间都大大地减少了,尤其是对于线性核和多项式核来说。其次,rbf 表现出了非常优秀的结果。经过我们的探索,我们可以得到的结论是:
- 线性核,尤其是多项式核函数在高次项时计算非常缓慢
- rbf 不擅长处理量纲不统一的数据集
幸运的是,这两个缺点都可以由数据无量纲化来解决。因此,SVM 执行之前,非常推荐先进行数据的无量纲化! 到了这一步,我们是否已经完成建模了呢?虽然 rbf 效果已经很好了,但还没有胜过两个两个线性核,但是不要忘了它还有很多核函数相关参数可以调整,接下来我们就来看看这些参数。
1.4 参数优化
在知道如何选取核函数后,我们还要观察一下除了 kernel 之外的核函数相关的参数。对于线性核函数,“kernel"是唯一能够影响它的参数,但是对于其他三种非线性核函数,他们还受到参数 gamma,degree 以及 coef0 的影响。 让我们再看一下各类核函数的表达式:
| 输入 | 含义 | 解决问题 | 核函数的表达式 | 参数 gamma | 参数 degree | 参数 coef0 |
|---|---|---|---|---|---|---|
| “linear” | 线性核 | 线性 | No | No | No | |
| ”poly” | 多项式核 | 偏线性 | Yes | Yes | Yes | |
| “sigmoid” | 双曲正切核 | 非线性 | Yes | No | Yes | |
| “rbf” | 高斯径向基 | 偏非线性 | Yes | No | No |
参数 gamma 就是表达式中的 γ,degree 就是多项式核函数的次数 d,参数 coef0 就是常数项 r。其中,高斯径向基核函数受到 gamma 的影响,而多项式核函数受到全部三个参数的影响。
| 参数 | 描述 |
|---|---|
| degree | 整数,可不填,默认 3 多项式核函数(’poly’)的次数,如果核函数没有选择 "poly",这个参数会被忽略 |
| gamma | 浮点数,可不填,默认'auto" 核函数的系数,仅在参数 kernel 的选项为”rbf“ , ”poly“ 和 ”sigmoid“ 的时候有效 输入”auto”,自动使用 1/(n_features) 作为 gamma 的取值 输入“scale”,则使用 1/(n_features*X.std() 作为 gamma 的取值 输入”auto_deprecated",则表示没有传递明确的 gamma 值(不推荐使用) |
| coef0 | 浮点数,可不填,默认 = 0.0 核函数中的常数项,它只在参数 kernel 为 poly 和 sigmoid 的时候有效。 |
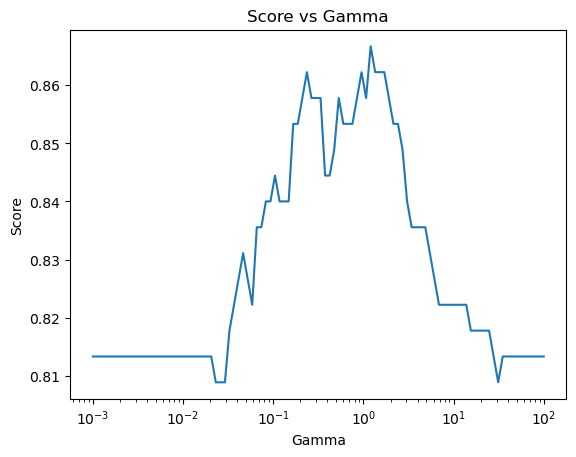
1.4.1 rbf 核|搜索最佳的 gamma 值
The best parameters is 1.2045035402587825 with a score of 0.8666666666666668
1.4.2 多项式核|使用网格搜索
由于多项式核函数涉及的参数更多,我们使用 sklearn 的网格搜索功能,对 degree, gamma, coef0 三个参数进行穷尽搜索。
由于 degree 加入后参数搜索较慢,我们先设置 degree = 1,对 gamma, coef0 两个参数进行穷尽搜索。
The best parameters are {'coef0': 0.0, 'gamma': 1.2742749857031335} with a score of 0.8523076923076923
00:14:038359
练习|下面,我们加入 degree 参数,对 degree, gamma, coef0 三个参数进行搜索,欢迎读者根据上述示例自行完成代码,进行课后练习。
课后练习答案:网格搜索
# ##################### Timing Warning:> 8 hours #########################
from sklearn.model_selection import StratifiedShuffleSplit
from sklearn.model_selection import GridSearchCV
degree_range = np.linspace(1,2,2)
gamma_range = np.logspace(-2,2,20)
coef0_range = np.linspace(0,5,20)
param_grid = dict(degree = degree_range, gamma = gamma_range, coef0 = coef0_range)
time0 = time()
cv = StratifiedShuffleSplit(n_splits=5, test_size=0.2, random_state=0)
grid = GridSearchCV(SVC(kernel="poly"), param_grid=param_grid, cv=cv)
grid.fit(Xs, Y)
print(f"The best parameters are {grid.best_params_} with a score of {grid.best_score_}")
print(datetime.datetime.fromtimestamp(time()-time0).strftime("%M:%S:%f"))
1.5 小结
到了这里,我们就得到了一个表现较好的 SVM 模型。
SVM 的优势在于其具有强大的学习能力的同时也具有较快的计算速度。但是面对特征量较多,较为“臃肿”的数据,由于其核函数需要升维处理,这会极大的影响其计算速度,甚至导致其不收敛(得不出训练结果),这种情况下只能使用不带核函数的支持向量机,但这会使 SVM 的效果大打折扣。因此对于 SVM 在材料中的应用时应优先考虑其数据集中特征数 n 与样本数 m 的比例,一般有以下选用原则:
- 如果相较于 𝑚 而言,𝑛 要大许多,即训练集数据量不够支持我们训练一个复杂的非线性模型,我们选用逻辑回归模型或者不带核函数的支持向量机。
- 如果 𝑛 较小,而且 𝑚 大小中等,例如 𝑛 在 1-1000 之间,而 𝑚 在 10-10000 之间,使用高斯核函数的支持向量机。
- 如果 𝑛 较小,而 𝑚 较大,例如 𝑛 在 1-1000 之间,而 𝑚 大于50000,则使用支持向量机会非常慢,解决方案是创造、增加更多的特征,然后使用逻辑回归或不带核函数的支持向量机。
SVM 的优点:
- SVM是一个凸优化问题,求得的解一定是全局最优。
- 不仅适用于线性线性问题还适用于非线性问题。
- 拥有高维样本空间的数据也能用SVM,这是因为数据集的复杂度只取决于支持向量而不是数据集的维度,这在某种意义上避免了“维数灾难”。
- 理论基础比较完善(例如神经网络就更像一个黑盒子)。
SVM 的缺点:
- 涉及m阶矩阵的计算(m为样本的个数), 因此SVM不适用于超大数据集。
- 只适用于二分类问题(多分类问题需要使用相应策略,如ovo和ovr)。
2 实践案例|SVM 预测高熵合金相态(分类)
2.1 案例背景
高熵合金(HEAs)是一类独特的多主元素合金(MPEAs),可以作为单相固溶体结晶。自 2004 年被提出以来,HEAs 引起了广泛的关注,不仅因为其优越的性能,还因为它为合金设计开辟了一个广阔的新领域。到目前为止,MPEAs 的组成空间中极小的部分已经通过试错方法进行了研究,周期表中有 80 多种金属元素,有效识别 MPEAs 的相位并找到所有可能的 HEA 组成是一个巨大的挑战。目前,研究人员使用高配位熵、混合焓、原子尺寸差等参数来识别HEAs,但这些参数并不稳健。热力学计算方法(如CALPHAD)和第一性原理计算在计算相稳定性方面更有效,但受限于计算成本和数据范围。机器学习(ML)在从现有数据中提取隐含关系方面表现出优势。支持向量机(SVM)是另一种著名的 ML 算法,它需要较少的训练样本,并具有许多内在优点,包括良好的理论基础、凸性、优秀的泛化能力和高计算速度。因此,这项研究采用了机器学习方法,构建了一个支持向量机(SVM)模型,将该模型应用于 16 个元素的组成空间,预测了多种高熵合金的相态。[2.2]
2.2 数据集介绍
在这里,我们选择参考文献 [2.3] 中的数据集,该数据集收集了 408 个经实验合成的 MPEA 样品,包含 648 个微观结构表征。我们只考虑最常见的铸态样品,以排除加工条件和热力学处理的影响。排除含有稀土元素或轻元素(除 Al 外)的样品以及相不确定的样品,以降低复杂性。不考虑密堆积六方 HEA,因为它们通常包含稀土元素。
然后,我们得到了一个包含 322 个不同铸态 MPEA 样品的数据集,其中包含 3-9 个组分元素。其中,有 18 个样品具有单个 BCC 相,43 个样品具有单个 FCC 相。其余的 261 个样品具有多相、金属间化合物或非晶相,用“NSP”标记,表示“不形成单相固溶体”。三元到九元 MPEA 的百分比以及 BCC、FCC 和 NSP 相的比例如图 (a) 所示。大多数样品由五个或六个元素组成,而单相 HEA 仅占很小一部分。数据集中有 18 个元素(Al、Ti、V、Cr、Mn、Fe、Co、Ni、Cu、Y、Zr、Nb、Mo、Ag、Hf、Ta、W 和 Au),它们的出现次数如图 (b) 所示。我们发现 Fe、Ni、Cr、Co 和 Al 在 200 个以上的样品中出现,而 Hf、Ag 和 Au 仅出现一次。

特征构建|MPEAs的热力学参数被用作候选特征,可以通过以下方程计算:
其中,、、、 和 分别表示第 i 个元素的摩尔分数、原子半径、熔点、价电子浓度和 Pauling 电负性。N 是组成元素的数量,R 是气体常数。 是二元液态合金的混合焓,来源于 Miedema's 理论 [3]。
最稳定的二元化合物的形成焓 可以从参考文献 [4] 中得出,也被认为是候选特征。所有样品的特征都经过归一化处理:
2.3 数据预处理
导入数据集
| Alloy | VEC | Tm | HIM | rd | ΔH | SC | χd | Ref. | Phase | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | HfNbTiZr | 4.25 | 2331.25 | -22 | 0.05 | 3.59 | 1.39 | 0.09 | [S1] | BCC |
| 1 | MoNbTaW | 5.50 | 3157.75 | -193 | 0.02 | -9.90 | 1.39 | 0.19 | [S2] | BCC |
| 2 | NbTaTiV | 4.75 | 2541.00 | -122 | 0.04 | -0.11 | 1.39 | 0.03 | [S3] | BCC |
| 3 | Al0.25NbTaTiV | 4.65 | 2446.41 | -428 | 0.04 | -10.75 | 1.53 | 0.03 | [S3] | BCC |
| 4 | Al0.5NbTaTiV | 4.56 | 2362.33 | -428 | 0.04 | -19.08 | 1.58 | 0.03 | [S3] | BCC |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 317 | CoCrCuFeMnNiTiV | 7.50 | 1811.00 | -435 | 0.05 | -12.11 | 2.08 | 0.09 | [S10] | NSP |
| 318 | Al0.125CoCrCuFeMnNiTiV | 7.43 | 1797.49 | -677 | 0.06 | -14.12 | 2.13 | 0.09 | [S10] | NSP |
| 319 | Al0.125CoCrCuFeNiTiMnV | 7.43 | 1797.49 | -677 | 0.06 | -14.12 | 2.13 | 0.09 | [S10] | NSP |
| 320 | Al0.67CoCrCuFeMnNiTiV | 7.15 | 1743.15 | -677 | 0.06 | -21.53 | 2.19 | 0.08 | [S10] | NSP |
| 321 | Al0.67CoCrCuFeNiTiMnV | 7.15 | 1743.15 | -677 | 0.06 | -21.53 | 2.19 | 0.08 | [S10] | NSP |
322 rows × 10 columns
让我们挑选两个特征,在低维空间中可视化查看数据的分布情况。在这里,我们绘制了 和 两个向量空间
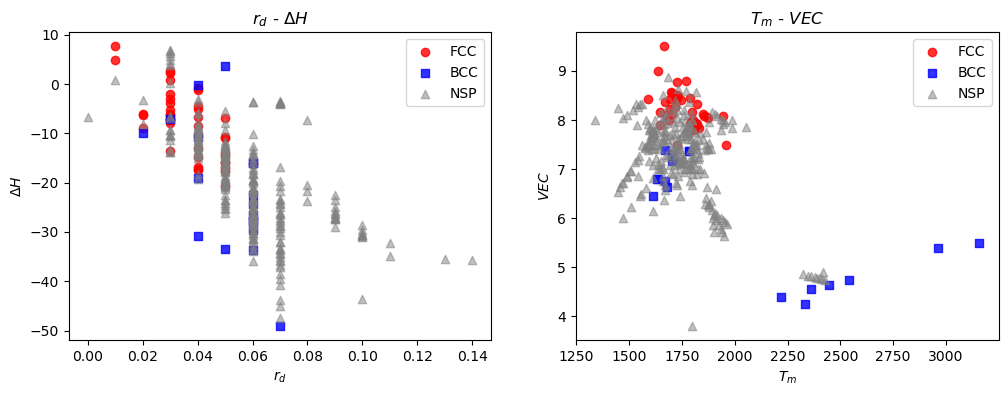
在 空间中,我们发现样本高度重叠且相位无法区分。在 空间中,VEC 似乎可以很好地区分 BCC 和 FCC 样本,但仍无法区分单相样本和 NSP 样本。
2.4 模型参数
支持向量机(SVM)模型是使用 Scikit-Learn 库构建的。径向基函数(Radial basis function,RBF)
被用作核函数,其中 表示第 个(第 个)样本的特征, 是核系数。模型训练采用了惩罚参数 。通过使用核函数,输入数据可以映射到高维甚至无限维空间,然后构造和优化超平面和支持向量以区分不同类别。一对一方法用于多分类问题(SVC 函数中默认该方法处理多分类问题)[6]。所采用的数据集包含322个经过铸造的高熵合金样本,其中 90% 用于训练,剩下的 10% 用于测试。采用 10 折交叉验证来评估 SVM 模型的性能:将训练集随机分成10个不相交的子集,依次将其中九个用于训练,剩下的一个用于验证。因此,训练(交叉验证)准确率被定义为10个训练(交叉验证)准确率的平均值。通过网格搜索方法优化 G 和 C :取G和C的值为和 ( 和 ),并选择实现最高验证准确率的 和 对。
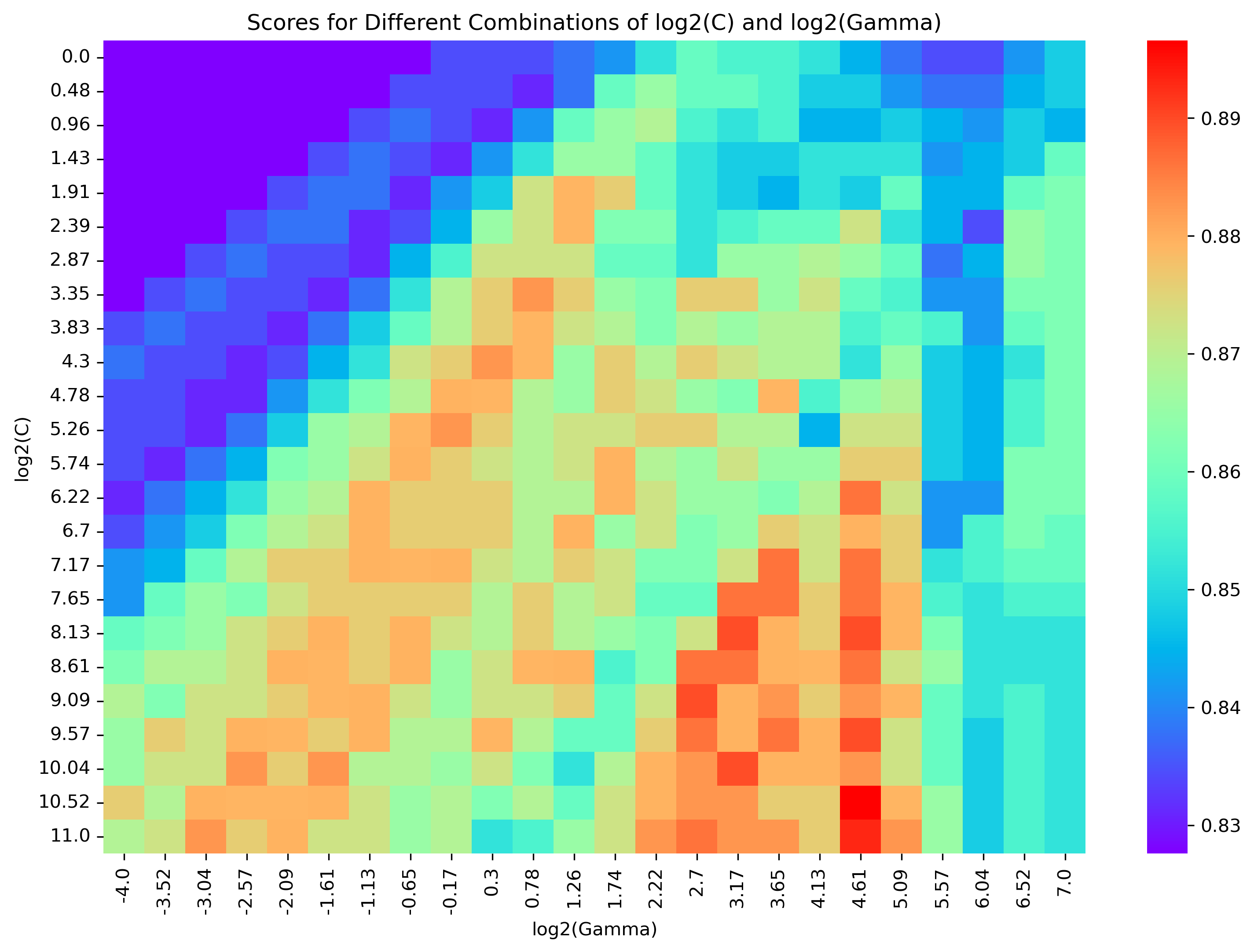
The best parameters are {'C': 1470.141322413518, 'gamma': 24.398078943191457}
with a score of 0.8965517241379309
Training Time: 00:22:648997
网格搜索的热力学图可视化
2.5 特征工程
接下来,我们使用上述样本和候选特征构建了一个 SVM 模型,并进行了前向特征搜索过程。
特征集从一个空集开始,然后,候选特征一个接一个地放入特征集。当包含一个特征时,具有 的 SVM 模型达到最高的 CV 精度,配置熵 的 CV 精度最低。在寻找第二个特征时,其余特征依次与 VEC 组合,特征子集 {VEC,rd} 达到最高精度。类似地,剩余特征被依次选出。当包含更多特征时,由于过拟合,验证精度会降低。
最后,特征子集 达到全局最高的 CV 精度。
Features: ['VEC'],
Score: 0.8655172413793103,
Best Parametric: {'C': 103.65545083522001, 'gamma': 128.0}
Features: ['Tm'],
Score: 0.8310344827586207,
Best Parametric: {'C': 7.308448734856074, 'gamma': 33.98806965960612}
Features: ['HIM'],
Score: 0.8275862068965518,
Best Parametric: {'C': 1.0, 'gamma': 0.0625}
Features: ['rd'],
Score: 0.8310344827586207,
Best Parametric: {'C': 2.7034142736280864, 'gamma': 91.88383265084488}
Features: ['ΔH'],
Score: 0.8482758620689654,
Best Parametric: {'C': 280.22362532728795, 'gamma': 65.95811486412865}
Features: ['SC'],
Score: 0.8310344827586207,
Best Parametric: {'C': 74.40828201477521, 'gamma': 128.0}
Features: ['χd'],
Score: 0.8344827586206897,
Best Parametric: {'C': 1.0, 'gamma': 17.513976582955497}
Round 1:
Max score: 0.8655172413793103
Selected features: ['VEC']
Best Parametric: {'C': 1.0, 'gamma': 17.513976582955497}
------------------------------
Features: ['VEC', 'Tm'],
Score: 0.8655172413793103,
Best Parametric: {'C': 74.40828201477521, 'gamma': 128.0}
Features: ['VEC', 'HIM'],
Score: 0.8724137931034482,
Best Parametric: {'C': 1055.3298378260583, 'gamma': 91.88383265084488}
Features: ['VEC', 'rd'],
Score: 0.8862068965517242,
Best Parametric: {'C': 757.5605485175992, 'gamma': 65.95811486412865}
Features: ['VEC', 'ΔH'],
Score: 0.8862068965517242,
Best Parametric: {'C': 14.182962020497952, 'gamma': 24.398078943191457}
Features: ['VEC', 'SC'],
Score: 0.8793103448275863,
Best Parametric: {'C': 2048.0, 'gamma': 33.98806965960612}
Features: ['VEC', 'χd'],
Score: 0.8448275862068966,
Best Parametric: {'C': 280.22362532728795, 'gamma': 2.3964013730337004}
Round 2:
Max score: 0.8862068965517242
Selected features: ['VEC', 'rd']
Best Parametric: {'C': 280.22362532728795, 'gamma': 2.3964013730337004}
------------------------------
Features: ['VEC', 'rd', 'Tm'],
Score: 0.8793103448275863,
Best Parametric: {'C': 53.41342291001935, 'gamma': 65.95811486412865}
Features: ['VEC', 'rd', 'HIM'],
Score: 0.886206896551724,
Best Parametric: {'C': 74.40828201477521, 'gamma': 2.3964013730337004}
Features: ['VEC', 'rd', 'ΔH'],
Score: 0.9,
Best Parametric: {'C': 14.182962020497952, 'gamma': 47.34753428234995}
Features: ['VEC', 'rd', 'SC'],
Score: 0.8965517241379309,
Best Parametric: {'C': 10.181132099880642, 'gamma': 128.0}
Features: ['VEC', 'rd', 'χd'],
Score: 0.8620689655172413,
Best Parametric: {'C': 2.7034142736280864, 'gamma': 128.0}
Round 3:
Max score: 0.9
Selected features: ['VEC', 'rd', 'ΔH']
Best Parametric: {'C': 2.7034142736280864, 'gamma': 128.0}
------------------------------
Features: ['VEC', 'rd', 'ΔH', 'Tm'],
Score: 0.9,
Best Parametric: {'C': 38.342421968539206, 'gamma': 24.398078943191457}
Features: ['VEC', 'rd', 'ΔH', 'HIM'],
Score: 0.9103448275862069,
Best Parametric: {'C': 201.15641167488735, 'gamma': 2.3964013730337004}
Features: ['VEC', 'rd', 'ΔH', 'SC'],
Score: 0.8965517241379312,
Best Parametric: {'C': 201.15641167488735, 'gamma': 12.57227572968046}
Features: ['VEC', 'rd', 'ΔH', 'χd'],
Score: 0.8999999999999998,
Best Parametric: {'C': 10.181132099880642, 'gamma': 17.513976582955497}
Round 4:
Max score: 0.9103448275862069
Selected features: ['VEC', 'rd', 'ΔH', 'HIM']
Best Parametric: {'C': 10.181132099880642, 'gamma': 17.513976582955497}
------------------------------
Features: ['VEC', 'rd', 'ΔH', 'HIM', 'Tm'],
Score: 0.9,
Best Parametric: {'C': 3.766027352595564, 'gamma': 12.57227572968046}
Features: ['VEC', 'rd', 'ΔH', 'HIM', 'SC'],
Score: 0.8896551724137931,
Best Parametric: {'C': 144.39860989827966, 'gamma': 0.6363207562425401}
Features: ['VEC', 'rd', 'ΔH', 'HIM', 'χd'],
Score: 0.9034482758620689,
Best Parametric: {'C': 74.40828201477521, 'gamma': 4.650517625923451}
Round 5:
Max score: 0.9034482758620689
Selected features: ['VEC', 'rd', 'ΔH', 'HIM', 'χd']
Best Parametric: {'C': 74.40828201477521, 'gamma': 4.650517625923451}
------------------------------
Features: ['VEC', 'rd', 'ΔH', 'HIM', 'χd', 'Tm'],
Score: 0.8965517241379309,
Best Parametric: {'C': 14.182962020497952, 'gamma': 2.3964013730337004}
Features: ['VEC', 'rd', 'ΔH', 'HIM', 'χd', 'SC'],
Score: 0.8931034482758621,
Best Parametric: {'C': 27.52381784051041, 'gamma': 0.886435126281122}
Round 6:
Max score: 0.8965517241379309
Selected features: ['VEC', 'rd', 'ΔH', 'HIM', 'χd', 'Tm']
Best Parametric: {'C': 27.52381784051041, 'gamma': 0.886435126281122}
------------------------------
Features: ['VEC', 'rd', 'ΔH', 'HIM', 'χd', 'Tm', 'SC'],
Score: 0.8965517241379309,
Best Parametric: {'C': 1470.141322413518, 'gamma': 24.398078943191457}
Round 7:
Max score: 0.8965517241379309
Selected features: ['VEC', 'rd', 'ΔH', 'HIM', 'χd', 'Tm', 'SC']
Best Parametric: {'C': 1470.141322413518, 'gamma': 24.398078943191457}
------------------------------
Test accuracy: 0.8484848484848485

更换不同的随机数种子,进行 10 次前向特征选择,将每次选择的特征进行加权处理,最终计算每个特征权重,并依据权重排序。
上一步的运算时间实在有点久! 我们这里直接将权重结果可视化展示:

反映了组成元素的电子特性; 表示由于不同原子半径产生的晶格应变的尺度;、 和 的组合描述了热力学性质。这里的特征选择过程暗示,电子和晶格应变的贡献可能比热力学效应更为主导。
参数 和 反映了形成金属间化合物的可能性。对于在数据集中占据大比例的 NSP 样本具有多个固溶相,它们没有被选出。
通过对MPEAs的电子、应变和热力学特征进行表征,特征子集{,,,,}应该对相的形成进行全面评估。
2.6 模型预测
高性能的 SVM 模型可以用于寻找新的高熵合金(HEAs)。我们首先考虑了数据集中的元素,因此选择了由 16 种元素(Al、Ti、V、Cr、Mn、Fe、Co、Ni、Cu、Y、Zr、Nb、Mo、Hf、Ta和W)组成的成分空间。当 N 从 3 到 8 时,共有 种元素组合。通过该模型,预测了所有这些候选者的相,并在其中得到了 369 种 FCC 和 267 种 BCC HEAs,它们包含 4 到 8 种组成元素。当 N = 4时,四元合金候选中的 HEAs 比例约为 5.44%。随着 N 的增加,由于形成金属间化合物的可能性增加,HEAs 的比例减少。HEAs 的数量继续增加,并在 N = 6 时达到最大值。此外,预测的大部分 BCC HEAs 由四或五种元素组成,而大部分 FCC 等原子 HEAs 由六或七种元素组成。
还记得 2.2 中各个特征的构造方式吗:
其中,、、、 和 分别表示第 i 个元素的摩尔分数、原子半径、熔点、价电子浓度和 Pauling 电负性。N 是组成元素的数量,R 是气体常数。 是二元液态合金的混合焓,来源于 Miedema's 理论 [3]。最稳定的二元化合物的形成焓 可以从参考文献 [4] 中得出,也被认为是候选特征。
建立一个高熵合金 Python 对象,方便快速获取相关性质
WARNING: Running pip as the 'root' user can result in broken permissions and conflicting behaviour with the system package manager. It is recommended to use a virtual environment instead: https://pip.pypa.io/warnings/venv
Entropy: 11.52634446553133 Melting temperature: 3155.65 Valence electron concentration: 5.5 Atomic size ratio: 0.030386856273138245 Electronegativity difference: 0.25258661880630184
接下来,我们将遍历每个元素组合,并使用 HighEntropyAlloy 对象的方法来计算相应的性质。最后,我们将这些性质添加到 Dataframe 中。
元素数量在 3~9 之间的所有组合数量为:39066
由于 计算所需的 计算软件需要作者授权,这里我们使用特征子集 对合金的晶格类型进行预测。
建立该特征子集的 SVM 分类模型:
The best parameters are {'C': 1470.141322413518, 'gamma': 12.57227572968046}
with a score of 0.8909090909090909
Training Time: 00:28:359674
由于上一步骤运行的计算时间较长,我们已经运算完并将相关结果保存在数据文件夹中,在这里我们导入这个数据文件夹,并预测 16 种元素(Al、Ti、V、Cr、Mn、Fe、Co、Ni、Cu、Y、Zr、Nb、Mo、Hf、Ta和W)组成的成分空间
| Composition | SC | Tm | VEC | rd | χd | |
|---|---|---|---|---|---|---|
| Predicted_Phase | ||||||
| BCC | 3596 | 3596 | 3596 | 3596 | 3596 | 3596 |
| FCC | 901 | 901 | 901 | 901 | 901 | 901 |
| NSP | 34569 | 34569 | 34569 | 34569 | 34569 | 34569 |
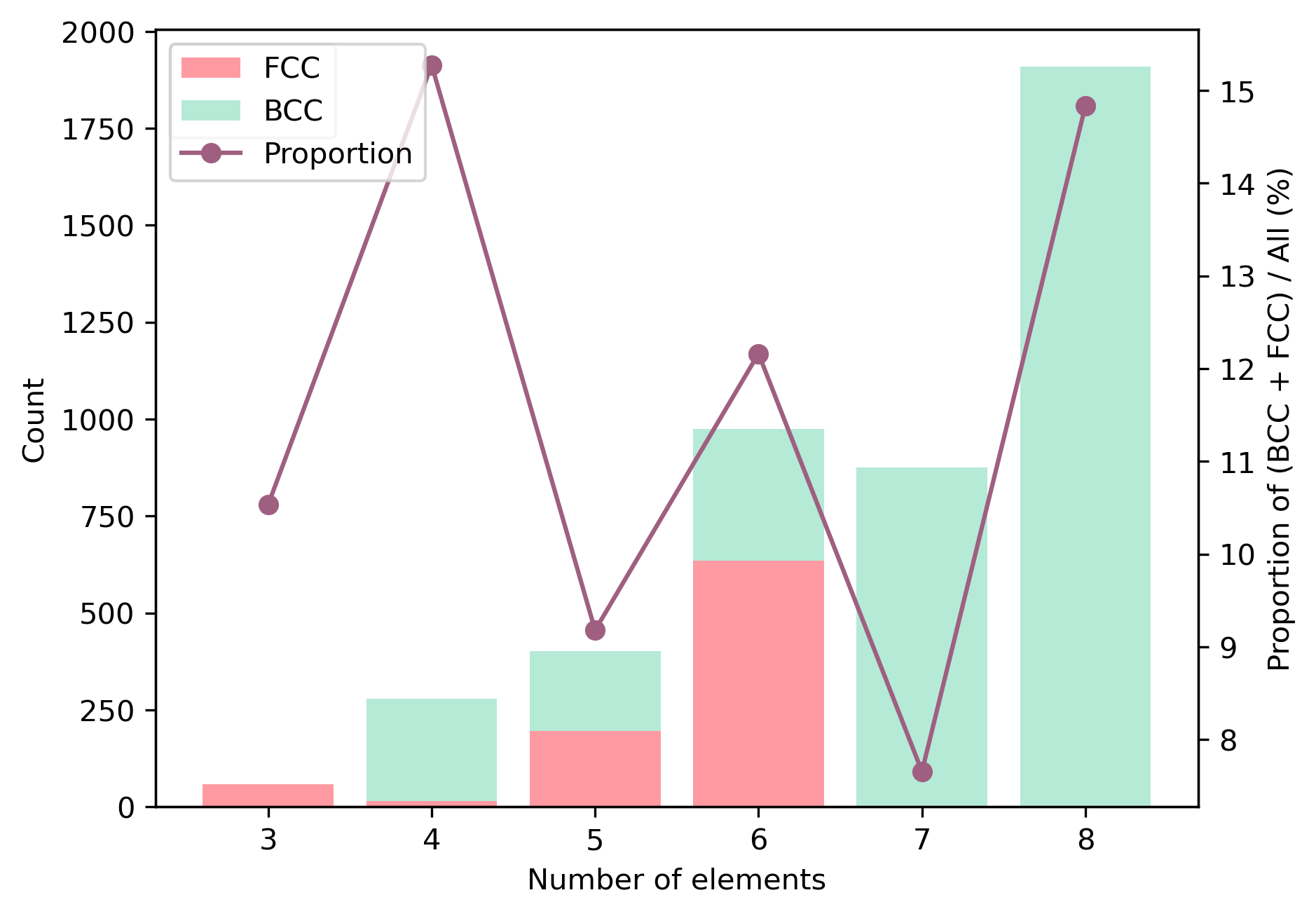
通过该模型,预测了所有这些候选成分的相,并在其中得到了 901 种 FCC 和 3596 种BCC HEAs,它们包含3到8种组成元素。
3 快速案例|SVM 预测生物炭材料废水处理性能(回归)
3.1 案例背景
水被认为是人类生活不可或缺的成分。根据全球水情报(GWI)的调查,全世界有超过12亿人没有清洁水可供使用。根据 Programme 和 UNWater 的统计(2009年),全世界平均每天有 200 多万吨工业、农业和生活废水排放到水环境中。废水严重影响人类健康,估计每天有 14,000 人死于废水。此外,废物对水的污染也是生物圈急剧变化的主要原因。根据科学家的说法,砷、镉、铬、铅、汞、杀虫剂和辐射是废水中的主要污染物。水资源短缺也推动了污染成分的浓度,水中重金属含量显著增加。因此,废水处理是一个严重影响人类健康的紧迫问题,需要整个社区的合作。
据研究,废水中的重金属是最危险和最难处理的问题。它们是造成人类健康风险和其他癌症(如肝癌、肺癌、胃癌)的最关键污染物。近年来,有几种去除重金属的方法,如物理化学方法(例如,机械筛选、流体动力分级、摩擦洗涤、磁分离、重力浓缩、浮选和静电分离、化学沉淀、离子交换和电化学沉积)、化学沉淀、膜过滤、混凝和絮凝、电渗析、电化学处理和生物方法。其中,生物方法(即生物炭系统)已被证实能最大限度地去除水/废水中的重金属。
根据之前研究人员的研究,生物炭系统的重金属吸附效率在很大程度上取决于其材料性质、金属来源和环境条件。因此,使用人工智能(AI)模型根据生物炭的特性、金属来源和环境条件等预测生物炭系统的重金属吸附效率(SEoHM),指出生物炭系统在水/废水中吸附重金属的可行性,对改善水质非常重要。
3.2 数据集介绍
为了开展这项研究,从之前的 12 项研究中收集了 353 项重金属吸附观测数据集。
数据集特征包括生物炭特征、吸附条件、重金属与生物炭的初始浓度比以及重金属特征。然而,重金属的性质,如离子半径、电荷数和电负性,表明与重金属的吸附效率不显著(朱等人,2019)。因此,在本研究中,它们不用于预测 SEoHM(Sorption efficiency of heavy metals,种金属吸附效率)。相反,本研究采用 13 个考虑生物炭特性,金属源,环境条件的输入变量对 SEoHM 进行预测,如生物炭表面积(BSA)、灰分百分比(A)、阳离子交换容量(CEC)、生物炭粒度(PSB)、废水中生物炭的pH值(pHww)、生物炭中碳的百分比(C)、氧碳比(O/C)、氢碳比(H/C)、氧氮与碳的比值[(O~N)/C]、溶液pH值(pHsol)、废水中重金属浓度(CO)、热解温度(TP)、环境温度(Tenvi)。因变量为重金属吸附效率(SEoHM)。
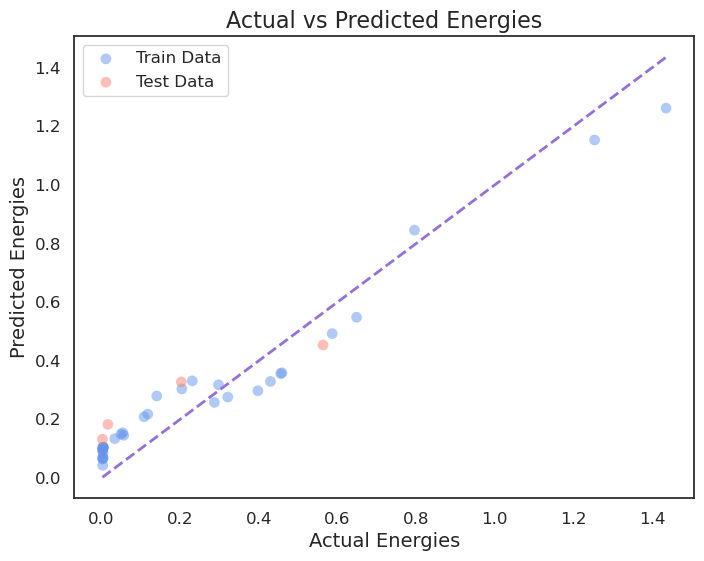
3.3 代码实现
The average accuracy under kernel linear is -0.38870686920126424 00:00:012162 The average accuracy under kernel poly is -0.2004902491068136 00:00:007593 The average accuracy under kernel rbf is 0.6345481566136117 00:00:006772 The average accuracy under kernel sigmoid is -0.8727672854453289 00:00:008205
4 参考
本案例第 1 节 SVM 可视化与核函数中使用了 Bilibili——菜菜 Sklearn 中的绘制技巧。
本案例中的数据集来自于论文:
生物炭数据集:Ke, B.; Nguyen, H.; Bui, X.-N.; Bui, H.-B.; Choi, Y.; Zhou, J.; Moayedi, H.; Costache, R.; Nguyen-Trang, T. Predicting the Sorption Efficiency of Heavy Metal Based on the Biochar Characteristics, Metal Sources, and Environmental Conditions Using Various Novel Hybrid Machine Learning Models. Chemosphere 2021, 276, 130204. https://doi.org/10.1016/j.chemosphere.2021.130204.
高熵合金案例:Li, Y.; Guo, W. Machine-Learning Model for Predicting Phase Formations of High-Entropy Alloys. Phys. Rev. Materials 2019, 3 (9), 095005. https://doi.org/10.1103/PhysRevMaterials.3.095005.
高熵合金数据集:Miracle, D. B.; Senkov, O. N. A Critical Review of High Entropy Alloys and Related Concepts. Acta Materialia 2017, 122, 448–511. https://doi.org/10.1016/j.actamat.2016.08.081.
Miedema's 理论:
F. D. Boer, R. Boom, W. C. M. Mattens, A. R. Miedema, andA.K.Niessen,inCohesion in Metals: Transition Metal Alloys, edited by F. R. de Boer and D. G. Pettifor, Vol. 1 (North-Holland, Amsterdam, 1988).
R. Zhang, S. Zhang, Z. He, J. Jing, and S. Sheng, Comput. Phys. Commun. 209, 58 (2016). https://doi.org/10.1016/j.cpc.2016.08.013
最稳定的二元化合物的形成焓 :
M. C. Troparevsky, J. R. Morris, P. R. C. Kent, A. R. Lupini, andG.M.Stocks,Phys. Rev. X 5, 011041 (2015). https://journals.aps.org/prx/abstract/10.1103/PhysRevX.5.011041
一对一方法(One-vs-One,简称OvO) 是一种处理多类分类问题的策略。在这种策略中,为每一对类别训练一个单独的分类器。具体来说,如果有 K 个类别,那么需要训练 K(K-1)/2 个二分类器。在测试阶段,根据所有 K(K-1)/2 个二分类器的投票结果来确定测试样本所属的类别。









