空间站广场

论文

Notebooks

比赛

课程

Apps

我的主页

我的Notebooks

我的论文库

我的足迹

我的工作空间

任务

节点

文件

数据集

镜像

项目

数据库

公开

SINDy: 从数据中反推系统的动力学

notebook

python

科学计算

从算法原理到代码实现

notebookpython科学计算从算法原理到代码实现

yefengcan@dp.tech

发布于 2023-09-25

推荐镜像 :Basic Image:ubuntu:22.04-py3.10-pytorch2.0

推荐机型 :c2_m4_cpu

导入依赖库

引子：开普勒与牛顿

算法介绍

代码实现

示例1: 二维振子

示例2：Lotka–Volterra模型

导入依赖库

代码

文本

[158]

import numpy as np

from scipy.integrate import odeint

import matplotlib.pyplot as plt

代码

文本

引子：开普勒与牛顿

开普勒在长期的观测中，收集了大量行星运动的数据，总结出了开普勒三大定律。但是，这些从数据中总结出的规律并没有解释行星椭圆轨道背后的原因。直到牛顿发现了牛顿定律，不仅解释了行星椭圆轨道背后的原因，也概括了一切宏观低速物体的运动规律。正是普适的动力学规律的发现，让人类能够在几百年后登上月球。

运用统计学、机器学习从数据中挖掘信息的方法（对应开普勒范式）在近年得到了长足的发展，但从数据中提取数据满足的动力学方程（对应于牛顿范式）进展则相对缓慢。这篇notebook介绍一种简单而有效的从动力学数据中反推系统满足的动力学方程的方法Sparse Identification of Nonlinear Dynamics (SINDy)，配合降噪以及降维的手段，该方法可以准确地还原出包括流体力学系统在内的复杂动力学系统的动力学方程。notebook只是用一个简单的例子简要说明该算法，如果想知道更多细节可以参考原文。

原文链接：https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4839439/

代码

文本

算法介绍

假定一个动力学系统满足微分方程：

$\frac{d}{d t} x (t) = f (x (t))$

从数据中可以搜集到系统在离散时间点的动力学轨迹。我们把轨迹按照下图所示的方式组织成矩阵：

alt image.png

其中 $\dot{X}$ 可以通过数值微分得到。SINDy的主要想法是用一系列基函数来展开 $f (x)$ 。基函数的选取有一定的任意性，通常需要考虑系统本身的对称性以及需要对物理过程的理解。例如，基函数可以包含多项式、三角函数以及指数函数等。我们将基函数在轨迹的各个时间点上的取值整理成下面的 $Θ$ 矩阵：

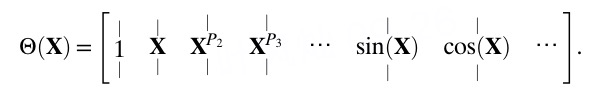
alt image.png

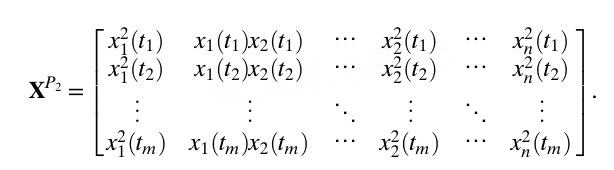
其中 $X^{P_{k}}$ 代表k次多项式。例如 alt image.png

我们假定 $f$ 可以用上面这些基函数近似。 $x$ 的第k个分量的动力学方程为 $\frac{d}{d t} x_{k} (t) = f_{k} (x_{k} (t))$ ，设 $f_{k}$ 用各基函数展开的系数向量为 $ξ_{k}$ ，设 $Ξ = [ξ_{1}, ξ_{2} ... ξ_{n}]$ ，那么

$\dot{X} = Θ (X) Ξ$

我们求解上面这个方程得到 $Ξ$ ，上面这个方程其实就描述了系统的动力学。在求解上面这个方程的过程中，算法假定 $Ξ$ 是稀疏的，也就是系统的动力学可以只由少数几项非线性项描述。因此在求解上面这个方程时，可以采用一种叫做sequential thresholded least-squares的方法：首先找到上面方程的最小二乘解作为初始猜测，然后将解当中小于某个阈值的元素全部设为0，然后再通过最小二乘估计估计其他非零项，如此反复直至收敛。原始论文中给出了该算法的matlab版本： alt image.png

下图概括了算法的全流程： alt image.png

代码

文本

代码实现

在这里，我们只选择多项式作为基函数。如果要加入三角函数、指数函数等是简单的，稍加修改即可。

代码

文本

[159]

def generate_polynomial(X, power):

if power == 0:

return np.ones_like(X)

elif X.shape[1] == 1:

return X ** power

poly = []

for p in range(power + 1):

poly.append((X[:, 0].reshape(-1, 1) ** (power - p)) * generate_polynomial(X[:, 1:], p))

return np.hstack(poly)

def generate_theta(X, max_power):

thetas = []

for p in range(max_power + 1):

thetas.append(generate_polynomial(X, p))

return np.hstack(thetas)

代码

文本

下面这段代码实现了sequential thresholded least-squares算法

代码

文本

[160]

def thresholded_least_square(X, X_dot, Theta, threshold, n_iter=10):

Xi = np.linalg.solve(Theta.T @ Theta, Theta.T @ X_dot)

n = X.shape[1]

for k in range(n_iter):

small_inds = np.abs(Xi) < threshold

Xi[small_inds] = 0

for i in range(n):

big_inds = np.logical_not(small_inds[:, i])

theta = Theta[:, big_inds]

Xi[big_inds, i] = np.linalg.solve(theta.T @ theta, theta.T @ X_dot[:, i])

return Xi

代码

文本

解出 $Ξ$ 后，反推出的系统动力学可以由下面的函数描述：

代码

文本

[161]

def inferred_dynamics(X, t, Theta, Xi):

return (Theta(X) @ Xi).reshape(-1)

代码

文本

示例1: 二维振子

这里我们考虑一个很简单的情形，考虑从数据中重建下面这个系统的动力学方程

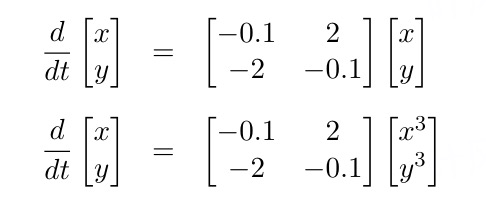
alt image.png

代码

文本

[6]

def linear_oscillator(x, t, K):

return x @ K.T

def nonlinear_oscillator(x, t, M):

return (x ** 3) @ M.T

代码

文本

先考虑线性的振子。我们数值给出系统的动力学轨迹：

代码

文本

[17]

x = np.array([2, 0])

t = np.linspace(0, 25, 500)

K = np.array([[-0.1, 2], [-2, -0.1]])

sol = odeint(linear_oscillator, x, t, args=(K,))

plt.plot(t, sol[:, 0])

plt.plot(t, sol[:, 1])

代码

文本

构造上面的 $X$ 和 $\dot{X}$ 矩阵。其中 $\dot{X}$ 由数值微分来估计：

代码

文本

[18]

X = (sol[:-1, :] + sol[1:, :]) / 2

dt = t[1] - t[0]

X_dot = (sol[1:, :] - sol[:-1, :]) / dt

代码

文本

构建基函数，这里我们用五次以内的多项式逼近:

代码

文本

[19]

Theta = generate_theta(X, 5)

代码

文本

用sequential thresholded least-squares方法求解，可以看出方法较为准确地还原出了上面的 $K$ 矩阵

代码

文本

[20]

Xi = thresholded_least_square(X, X_dot, Theta, 5e-2)

array([[ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [-0.10025119, -2.00166243],
       [ 2.00166244, -0.10025118],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ]])

代码

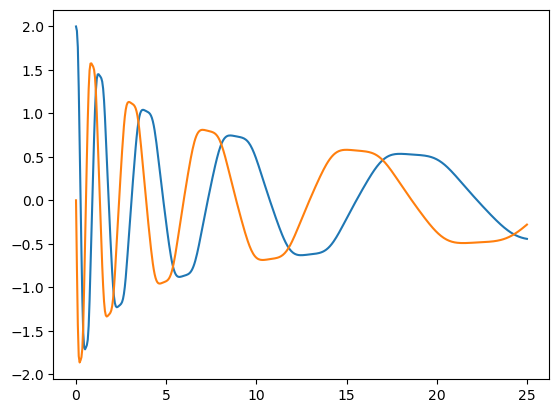
文本

我们对比一下反推出的轨迹和原始轨迹。我们可以发现二者吻合得很好

代码

文本

[21]

inferred = odeint(inferred_dynamics, x, t, args = (lambda X: generate_theta(X.reshape(1, -1), 5), Xi))

代码

文本

[22]

plt.plot(t, inferred[:, 0], '--')

plt.plot(t, inferred[:, 1], '--')

plt.plot(t, sol[:, 0])

plt.plot(t, sol[:, 1])

plt.xlabel('t')

plt.ylabel('x')

代码

文本

非线性振子的情况大同小异：

代码

文本

[7]

x = np.array([2, 0])

t = np.linspace(0, 25, 500)

K = np.array([[-0.1, 2], [-2, -0.1]])

sol = odeint(nonlinear_oscillator, x, t, args=(K,))

plt.plot(t, sol[:, 0])

plt.plot(t, sol[:, 1])

代码

文本

[8]

X = (sol[:-1, :] + sol[1:, :]) / 2

dt = t[1] - t[0]

X_dot = (sol[1:, :] - sol[:-1, :]) / dt

代码

文本

[9]

Theta = generate_theta(X, 5)

代码

文本

[11]

Xi = thresholded_least_square(X, X_dot, Theta, 5e-2)

array([[ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [-0.11181626, -2.02829761],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 2.02889589, -0.09706269],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ]])

代码

文本

[12]

inferred = odeint(inferred_dynamics, x, t, args = (lambda X: generate_theta(X.reshape(1, -1), 5), Xi))

代码

文本

[16]

plt.plot(t, inferred[:, 0], '--')

plt.plot(t, inferred[:, 1], '--')

plt.plot(t, sol[:, 0])

plt.plot(t, sol[:, 1])

plt.xlabel('t')

plt.ylabel('x')

代码

文本

示例2：Lotka–Volterra模型

Lotka-Volterra模型描述一个生态系统中两个物种（捕食者与猎物）之间的相互作用。设 $x$ 为猎物的种群密度， $y$ 为捕食者的种群密度，系统的动力学由下面的微分方程组描述：

$\frac{d x}{d t} = αx - β x y$

$\frac{d y}{d t} = δ x y - γ y$

代码

文本

[228]

def Lotka_Volterra_model(X, t, alpha, beta, delta, gamma):

x, y = X[0], X[1]

return np.array([alpha * x - beta * x * y, delta * x * y - gamma * y])

代码

文本

[229]

x = np.random.uniform(low=0, high=1, size=(2, ))

t = np.linspace(0, 100, 500)

代码

文本

[230]

parameter_set = tuple(np.random.uniform(size = (4,)))

sol = odeint(Lotka_Volterra_model, x, t, args = parameter_set)

代码

文本

[237]

plt.plot(sol[:, 0], label = 'prey')

plt.plot(sol[:, 1], label = 'predator')

plt.xlabel('t')

plt.ylabel('x')

plt.legend()

代码

文本

[232]

X = (sol[:-1, :] + sol[1:, :]) / 2

dt = t[1] - t[0]

X_dot = (sol[1:, :] - sol[:-1, :]) / dt

Theta = generate_theta(X, 5)

代码

文本

[233]

Xi = thresholded_least_square(X, X_dot, Theta, 5e-2)

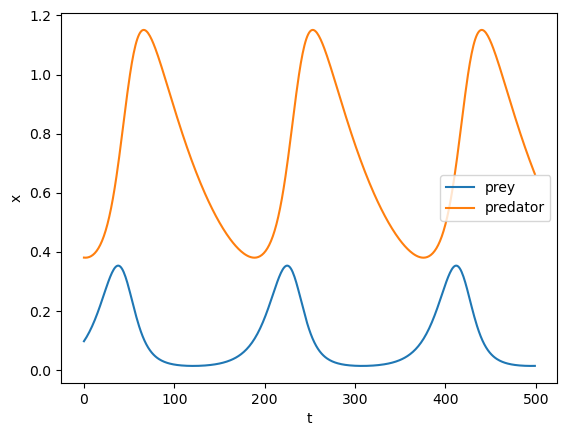
array([[ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.51205957,  0.        ],
       [ 0.        , -0.0676224 ],
       [ 0.        ,  0.        ],
       [-0.73575856,  0.64090381],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ]])

代码

文本

[234]

parameter_set

(0.512015496719407,
 0.7357229810974245,
 0.6408070224834814,
 0.06760830207119717)

代码

文本

可见推断出的参数与实际参数几乎一致

代码

文本

[235]

inferred = odeint(inferred_dynamics, x, t, args = (lambda X: generate_theta(X.reshape(1, -1), 5), Xi))

代码

文本

[236]

plt.plot(t, inferred[:, 0], '--')

plt.plot(t, inferred[:, 1], '--')

plt.plot(t, sol[:, 0])

plt.plot(t, sol[:, 1])

plt.xlabel('t')

plt.ylabel('x')

代码

文本

推断出的动力学与实际观测也高度吻合。

代码

文本

[ ]

代码

文本

notebook

python

科学计算

从算法原理到代码实现

notebookpython科学计算从算法原理到代码实现

点个赞吧

本文被以下合集收录

动力学

林灵鸿

更新于 2024-08-27

1 篇0 人关注

识别方程

lucky me

更新于 2023-11-28

1 篇0 人关注