空间站广场

论文

Notebooks

比赛

课程

Apps

我的主页

我的Notebooks

我的论文库

我的足迹

我的工作空间

任务

节点

文件

数据集

镜像

项目

数据库

公开

细看成岭又成峰——动力学轨迹的主成分分析

Scikit-Learn

pca

Molecular Dynamics

Tutorial

中文

notebook

Scikit-LearnpcaMolecular DynamicsTutorial中文notebook

Wentao

发布于 2023-07-10

数据集

AI4SCUP-CNS-BBB(v1)

细看成岭又成峰——分子动力学轨迹的主成分分析

作者: Wentao Guo guowentao@dp.tech

推荐镜像：bohrium-notebook

推荐计算资源：CPU

内容：本教程主要介绍 1.主成分分析(PCA, Principal Component Analysis) 2.通过主成分分析提取动力学轨迹的几何变化信息

使用方式: 您可在 Bohrium Notebook 上直接运行。您可以点击界面上方蓝色按钮 开始连接，选择 bohrium-notebook 镜像及任何一款节点配置，稍等片刻即可运行。如您遇到任何问题，请联系 bohrium@dp.tech 。

共享协议: 本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。

代码

文本

什么是主成分分析(PCA)?

主成分分析(PCA, Principal Component Analysis）是一种用于分析和简化数据集的统计技术，常用于降低数据的维度。它由卡尔·皮尔逊在1901年发明，是特征分析中最简单的多元统计方法之一。

PCA的核心其实就是两个字:降维.举个简单的例子,当我们在山峰的一侧观察的时候,眼睛(或相机)所接收到的信息就是由山峰投影在二维平面上的画面.这个降低维度的过程往往意味着信息的损耗.苏东坡在游览庐山时曾有感而发:

“横看成岭侧成峰,远近高低各不同”.

后人常对这《题西林壁》诗词进行深入的文学以及哲学分析,但这句话其实非常生动直接地体现了降维这一过程导致的结果:从一个投影面观察庐山时,山脚下不同位置游览者所看到的只能是“岭”或者是“峰”.但庐山的真面目,也就是完整的三维信息,即不仅仅是“岭”,也并不仅限于“峰”.

这里就自然而然的引发了一个有趣的思考:有没有一种观察角度,让我能以二维的形式,最大程度地获取庐山三维的信息呢? 看到这里的你其实已经充分理解了主成分分析的核心思想: 将原始高维数据投影至低维子空间数据的同时,最大程度地保留(与任务相关的)数据的信息 这种投影所基于的就是数据中最重要的特征,这些特征被称作主成分(PC, principal compotens),它们代表着原始数据中变化最大的方向.直观理解,主成分分析即是通过数学来抓取数据的特征,找到主成分(们)以便于后续的对数据进行操作和分析.

回到庐山的例子,根据主成分的信息,我们期待找到一个最好的观察庐山的(投影)角度 —— 在这个方向上我所看到的庐山的投影,能让我即看到“岭”,又看到”峰“,甚至能够在量化的角度上去描述庐山更像”岭“还是更像”峰“.

下面让我们一起欣赏一下庐山的3D建模图,你有没有发现从正面来看确实是长长山岭,而从侧面看就是险峻的山峰了?

代码

文本

代码

文本

如何实现主成分分析(PCA)?

作为一种重要的数据处理以及分析手段,很多学科都把主成分分析(PCA)作为必修内容,尤其以数学、数据驱动专业(统计学、计算机科学、数据科学等)为背景的同学想必对这一概念已了然于胸.由于其强大的普适性和直观性,主成分分析的功能在很多程序语言中都被打包为可直接调用的工具(比如python中的sklearn,R中的PCA功能).

下面我们会以公式和python代码结合的形式来对葡萄酒数据进行主成分分析,以帮助不熟悉的同学快速地理解主成分分析的具体操作.在这个过程中我们会使用sklean自带的wine数据集,通过对不同环境下产生的三种葡萄酒信息进行降维,以观察他们在13个属性上的差异(酒精浓度、苹果酸浓度、颜色强度、色调、脯氨酸浓度等).除了这13个属性外,数据中还保留了每一瓶酒的类别,我们会通过不同的颜色来区分这三类酒.该数据集中包含178瓶酒(样本)的信息.

代码

文本

[1]

# 载入需要的工具

import numpy as np

import sklearn

import matplotlib.pyplot as plt

from sklearn.preprocessing import StandardScaler

from sklearn.datasets import make_blobs

from mpl_toolkits.mplot3d import Axes3D

np.random.seed(0)

# 从sklearn的数据集中载入wine数据集

wine_data = sklearn.datasets.load_wine()

X = wine_data.data[:,:] # 载入每瓶酒(样本)的变量

y = wine_data.target # 载入每瓶酒酒(样本)的种类

print("样本数目为: ",len(y))

print("变量数目为: ",X.shape[1])

样本数目为:  178
变量数目为:  13

代码

文本

数据载入后,我们还需要一些前处理(preprocess)操作:标准化每个变量,使他们的均值为0,方差为1.

对数据的预操作(如归一化,标准化)可以使后续数据的分析更好.在PCA的任务下,标准化可以帮助我们解决:

量纲问题：数据集中的各个特征可能具有不同的单位和量纲，如长度单位可能是米、厘米等，重量单位可能是千克、克等。这些不同的单位在进行PCA时可能会导致某些特征对结果的影响过大。通过标准化，我们可以消除这种量纲带来的影响，使得各个特征具有相同的尺度。
方差问题：不同特征的方差可能差别很大，如果不进行标准化处理，那么方差较大的特征将主导PCA的结果，导致方差较小的特征被忽略。标准化后，所有特征的方差都变为1，从而避免了这个问题。
性能问题：标准化后的数据更容易满足很多算法（如梯度下降法）的假设和要求，从而能够提高模型的性能。
效率问题：标准化后的数据分布更为集中，有利于提高计算效率，加快PCA的计算速度。

代码

文本

[2]

# 第一步: 标准化数据集

X = StandardScaler().fit_transform(X)

代码

文本

我们首先引入方差的概念以帮助大家定量化地理解什么是“信息量”

在PCA中,信息量就是数据的多样性。比如对于一个全中国大学生的数据集合，数据集中第一个变量为大学生的年龄,第二个变量为大学生的高考分数.显然,我们能在第二个变量中获得的更多的信息量,因为大学生年龄相似(数据分散性小),但是高考分数不尽相同(数据分散性大)。

回到方差,我们从一维(单一变量)数据开始并逐渐拓展到多维(多变量)数据.

根据定义,我们可以通过求数据点与平均值的差的平方的均值来计算一维数据的方差(variance): $Va r (x) = \frac{1}{n} i = 1 \sum n (x_{i} - \overset{x}{ˉ})^{2}$

但是根据我们的预处理操作,数据标准化后,因为平均值被平移至0,数据的方差也被标准化为1,那么对于每一个变量来说: $Va r (\tilde{x}) = \frac{1}{n} i = 1 \sum n \tilde{x}_{i}^{2} = 1$

其中n为样本的总数,在这个例子中, $n = 178$

为了描述不同之间变量的相关性,我们这里引用协方差(covariance)来描述:

根据定义,每一对变量(这里以变量 $X_{a}$ , $X_{b}$ 为例,你可以想象为酒的酸度和甜度)的协方差计算公式: $C o v (x_{a}, x_{b}) = \frac{1}{n - 1} i = 1 \sum n \tilde{x}_{ai} * \tilde{x}_{bi}$

方差是协方差的一种特殊情况，即当两个变量是相同的情况。

那么为什么分母从 $n$ 变成了 $n - 1$ 呢?简单来说,当前 $n - 1$ 个值可以自由地放飞自我的时候,最后一个,也就是第 $n$ 个值必须老老实实地配合前 $n - 1$ 个值来满足均值的前提要求.因此第 $n$ 个数据没有信息量,它由前 $n - 1$ 个值和均值所决定,如果我们除以 $n$ 而非 $n - 1$ ,那么方差/协方差会比样本真实的情况偏小,当样本较大时,我们会将 $n - 1$ 近似为 $n$ .这其中其实暗含“有偏”和“无偏”的概念,感兴趣的朋友可以点击超链接自行探索.

那么怎么储存每一对协方差信息呢?这里我们利用协方差矩阵 $C$ 来表示: $C = \frac{1}{n} X X^{T}$

如果两变量的协方差为0,那么意味着他们线性不相关(正交),协方差的绝对值越大,说明两变量的线性相关性越强(如下图)

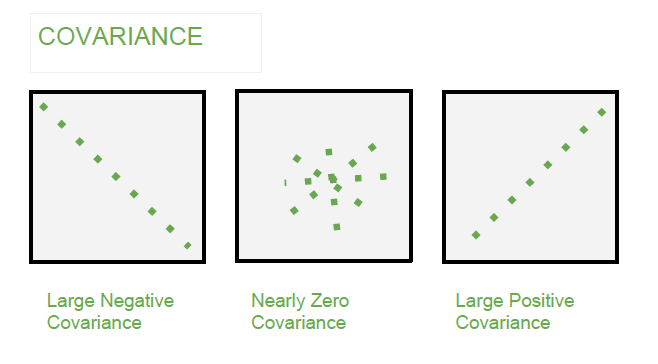
为了让主成分,也就是新变量能够保留更多的原始信息,我们需要主成分之间的线性相关性尽可能小.为了让降维后变量的线性相关性尽可能小,我们需要让每对不同变量的协方差为0,即让他们相互正交.那么现在我们的目标就变得更加清晰:我们需要通过一种变换方式令数据的协方差矩阵除对角以为的其他元素化为0,即矩阵对角化,从而得到新的主成分(们).

代码

文本

[3]

# 第二步: 计算变量矩阵X的协方差矩阵

cov_matrix = np.cov(X, rowvar=False)

#在这里协方差矩阵描述每一对变量的相关性,因此大小为13*13

print("协方差矩阵的形状",cov_matrix.shape)

协方差矩阵的形状 (13, 13)

代码

文本

下面就是见证奇迹的时刻——我们会将协方差矩阵的对角化

假设我们新的协方差矩阵为 $C_{n e w}$ ,原方差矩阵为 $C$ ,投影前的矩阵为 $X$ ,投影后的矩阵为 $PX = Z$ ,那么: $C_{n e w} = \frac{1}{n} Z Z^{T} = \frac{1}{n} (PX) (PX)^{T} = \frac{1}{n} PX X^{T} P^{T} = p (\frac{1}{n} X X^{T}) P^{T} = PC P^{T}$

根据协方差矩阵的表达式,我们可以得知它是一个实对称矩阵(以主对角线为对称轴，各元素对应相等的矩阵,根据 $C o v (x_{a}, x_{b}) = C o v (x_{b}, x_{a})$ ),因为方差/协方差非负.根据线性代数,实对称矩阵具有一个非常重要的特性:一个 $m$ 行 $m$ 列的实对称矩阵 $C$ 一定可以找到 $m$ 个正交特征向量,而这些特征向量通过堆叠组成矩阵 $E$ ,而 $E^{T} CE$ 则是一个对角化的矩阵.根据上面的公式,我们可以自然而然的联系 $P$ 和 $E$ .因此,我们将协方差对角化的问题转化为对 $C$ 的特征值分解问题.通过求解协方差矩阵的特征值( $C_{n e w}$ 对角元素)与特征向量(P)来得到新的成分.

注意操作到这里的时候我们只是把原变量线性变换为相互正交的变量(成分),并没有确定哪些是更重要的变量(主成分).

补充:有关实对称矩阵的相关知识点

代码

文本

[4]

# 第三步: 求解协方差矩阵的特征值和特征向量

eigenvalues, eigenvectors = np.linalg.eigh(cov_matrix)

print("特征值的数目:",len(eigenvalues)) # 特征值的数目和原数据的变量数一致

print("特征值:",eigenvalues)

print("特征向量矩阵的形状:",eigenvectors.shape) # 特征矩阵为13*13的实对称矩阵

特征值的数目: 13
特征值: [0.10396199 0.16972374 0.22706428 0.25232001 0.29051203 0.35046627
 0.55414147 0.64528221 0.85804868 0.92416587 1.45424187 2.51108093
 4.73243698]
特征向量矩阵的形状: (13, 13)

代码

文本

代码

文本

之后,我们将特征向量按其对应的特征值从大到小排列.

代码

文本

[5]

# 第四步: 根据特征值从大到小排列其对应的特征向量

sorted_indices = np.argsort(eigenvalues)[::-1]

sorted_eigenvalues = eigenvalues[sorted_indices]

sorted_eigenvectors = eigenvectors[:, sorted_indices]

print("排序后的特征值:",sorted_eigenvalues)

排序后的特征值: [4.73243698 2.51108093 1.45424187 0.92416587 0.85804868 0.64528221
 0.55414147 0.35046627 0.29051203 0.25232001 0.22706428 0.16972374
 0.10396199]

代码

文本

那么特征值怎么能够代表特征向量对于协方差大小的贡献呢?

根据矩阵乘法的定义,我们知道:

$A = [a_{11} a_{12} a_{13}]$

$B = b_{11} b_{21} b_{31} b_{12} b_{22} b_{32}$

$C = A B = [a_{11} b_{11} + a_{12} b_{21} + a_{13} b_{31} a_{11} b_{12} + a_{12} b_{22} + a_{13} b_{32}]$

在这个过程中,运算可以被看作是一种投影,即将二维矩阵 $B$ 的每一个元素变换到以 $A$ 向量所代表的空间去,而C即是投影的结果.在这个过程中,只要A比B的维度小,那么投影出的C便实现了对B的降维.而C中元素值的大小就是将B投影后的标量大小.当我们在对角化协方差矩阵的时候,其中矩阵乘法的部分恰恰符合投影的思路——协方差矩阵投影后,标量越大的特征值对应着特征向量的方向方差越大.

假设我们的特征值为 $λ_{1}, λ_{2} ... λ_{13}$ ,特征向量为 $u_{1}, u_{2} ... u_{13}$ ,总方差为 $S$ ,那么满足:

$i = 1 \sum 13 λ = S$

在我们的例子中总方差为 $S = 13$

同时,我们用更通用的解释方差explained variance来度量数据集中多少变化可以归因于每个主成分（特征向量). $E x pl ain e d Va r ian ce = \frac{λ _{i}}{\sum _{i = 1}^{13} λ _{i}}$

代码

文本

根据特征值的大小,我们将提取最靠前的K个特征向量(主成分!)以构成投影的子空间.

为了能够直观的看到降维后的数据,我们选择维度=2,也就是保留特征值第一大和第二大的特征向量.

代码

文本

[6]

# 为了更好的理解特征值和总方差的关系,让我们看一看特征值的和是否为总方差

# 注意因为我们已经标准化了数据,那么在每一维上的方差都为1,而十三维数据的总方差为13

# 将所有特征值加起来:

print("特征值的和:",sum(sorted_eigenvalues))

特征值的和: 13.073446327683616

代码

文本

我们将提取最靠前的K个特征向量以构成投影的子空间.为了能够直观的看到降维后的数据,我们选择维度=2,也就是保留特征值第一大和第二大的特征向量

代码

文本

[7]

# 第五步: 选择排序最前的k对特征值及特征向量

k = 2

selected_eigenvectors = sorted_eigenvectors[:, :k]

#为了得到投影后的新变量,我们也只需要用矩阵内积的运算$Z = PX$

# 第六步: 将原来的数据投影在上一步所选特征向量所组成的 K=2 维空间上

X_pca = np.dot(X, selected_eigenvectors)

代码

文本

通过绘图我们可以可视化对样本变量降维的结果.

代码

文本

[8]

# 第七步: 通过画图可视化结果,我们将呈现一张2*2的大图,同时每次会在大图中加入一张小图

fig = plt.figure(figsize=(10, 10))

# 图一:以前三个变量为三维坐标的散点图

ax = fig.add_subplot(221, projection='3d')

ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=y)

# 在散点图中画出前两个主成分(特征向量)代表的方向

for length, vector in zip(sorted_eigenvalues[:2], sorted_eigenvectors.T[:2]):

v = vector * 2 * np.sqrt(length)

plt.plot([0, v[0]], [0, v[1]], '-k', lw=3)

ax.set_xlabel('x1') # 设置X轴名称:变量X1

ax.set_ylabel('x2') # 设置Y轴名称:变量X2

ax.set_zlabel('x3') # 设置Z轴名称:变量X3

plt.title('Figure1: 3D Visualization of Real Data with PCA vectors') # 设置图一标题

# 图二: 以x1,x2为变量画出二维散点图

ax = fig.add_subplot(222)

ax.scatter(X[:, 0], X[:, 1], c=y)

ax.set_xlabel('x1') # 设置X轴名称:变量X1

ax.set_ylabel('x2') # 设置Y轴名称:变量X2

plt.title('Figure2: 2D Projection on x1 and x2') # 设置图二标题

# 图二: 以x1,x3为变量画出二维散点图

ax = fig.add_subplot(223)

ax.scatter(X[:, 0], X[:, 2], c=y)

ax.set_xlabel('x1') # 设置X轴名称:变量X1

ax.set_ylabel('x3') # 设置X轴名称:变量X3

plt.title('Figure3: 2D Projection on x1 and x3') # 设置图三标题

# 图四画出投影在第一主成分和第二主成分的二维散点图

ax = fig.add_subplot(224)

ax.scatter(X_pca[:, 0], X_pca[:, 1], c=y)

ax.set_xlabel('First Principal Component (PC1)') # 设置X轴名称:第一主成分

ax.set_ylabel('Second Principal Component (PC2)') # 设置Y轴名称:第二主成分

plt.title('Figure4: Visualization of PCA result') # 设置图四标题

plt.show()

代码

文本

图一是根据前三个变量(酒精浓度、苹果酸含量、含灰量)画出的所有样本分布,可以看出三种酒之间并没有明显的边界,但在空间上它们的确有所区分.

如果将数据直接投影在两种变量空间上:如图2酒精浓度 $x_{1}$ 和苹果酸含量 $x_{2}$ ,图3酒精浓度 $x_{1}$ ,含灰量 $x_{3}$ ,我们可以发现在牺牲其他维度信息后,数据的特征几乎完全不能够被保留.

图四则是将样本投影在第一特征向量(主成分PC1)和第二特征向量(主成分PC2)的数据结果.可以看出在方差最大(PC1)和第二大(PC2)方向的投影下,样本的信息被保留的很好——三种酒在空间中的分布区域有着明显的分别.通过这一过程,高维的样本信息通过有效压缩被三维生物(我们)直观地感受.

除此以外,我们还可以通过分解所得到的特征向量和特征值得到其他信息:

特征值决定了解释的总方差的比例：所有特征值的总和表示数据集中的总方差。每个特征值与特征值总和的比例表示由相应主成分解释的总方差的比例。
特征向量决定了数据集的坐标系,排在最前面的特征向量给出了样本数据变化最大的方向
特征向量提供了对特征重要性的洞察：特征向量包含原始特征的系数们,而这些系数的大小可以指示每个特征对主成分的贡献或重要性.

下面让我们看一看主成分的具体形式,以观察我们如何对于原始特征进行重构,以及特征值们对原数据方差的描述占比,并观察特征值的累积贡献度.

代码

文本

[9]

# 输出排序好的特征向量和相应的特征值 (注意这里排列好的特征向量从前往后就是从主至次的主成分们)

for ind,value in enumerate(sorted_eigenvectors):

print("第"+str(ind+1)+"的主成分为:",np.round(sorted_eigenvectors[ind],decimals=1),"\n"+"方差描述占比:",np.round(sorted_eigenvalues[ind]/sum(sorted_eigenvalues),decimals=2))

# 定义一个函数来可视化特征值累积贡献

def plot_cumulative_eigenvalues(eigenvalues):

# 计算累积特征值除以总特征值的比率

cumulative_sum = np.cumsum(eigenvalues)

total_sum = np.sum(eigenvalues)

cumulative_percentage = cumulative_sum / total_sum

# 画出累积特征值的分布

num_components = len(eigenvalues)

x = np.arange(1, num_components + 1) # X轴表示第几个特征值所对应的累积特征值

plt.plot(x, cumulative_percentage, marker='o')

# 设置轴坐标和标题

plt.xlabel('Number of Principal Components') # 设置X轴名称:主成分的累积数目

plt.ylabel('Cumulative Variance Explained') # 设置Y轴名称: 累积方差

plt.title('Cumulative Eigenvalue Contribution') # 设置图片标题

# 设置图的X轴,Y轴范围以及格点

plt.xlim(0, num_components+1) # 设置X轴范围

plt.ylim(min(cumulative_percentage)-0.1, 1.1) # 设置Y轴范围

plt.grid(True)

plt.show()

# 根据定义的函数画出酒数据集的累积特征值贡献

plot_cumulative_eigenvalues(sorted_eigenvalues)

第1的主成分为: [-0.1  0.5  0.2 -0.  -0.3 -0.2  0.1 -0.4  0.5  0.2  0.2  0.3  0. ] 
方差描述占比: 0.36
第2的主成分为: [ 0.2  0.2 -0.1  0.5  0.  -0.5 -0.4 -0.1 -0.1 -0.3 -0.1 -0.1  0. ] 
方差描述占比: 0.19
第3的主成分为: [ 0.   0.3 -0.6 -0.2 -0.1 -0.2  0.1  0.2 -0.3 -0.   0.5  0.  -0.1] 
方差描述占比: 0.11
第4的主成分为: [ 0.2 -0.  -0.6  0.1  0.1  0.1  0.3 -0.4  0.2  0.1 -0.5  0.1  0.1] 
方差描述占比: 0.07
第5的主成分为: [-0.1  0.3 -0.1 -0.4  0.7 -0.  -0.3  0.2  0.3  0.1 -0.1 -0.1  0.1] 
方差描述占比: 0.07
第6的主成分为: [-0.4  0.1 -0.1  0.2 -0.1  0.1  0.   0.4  0.3 -0.3 -0.3  0.3 -0.5] 
方差描述占比: 0.05
第7的主成分为: [-0.4 -0.  -0.2  0.2 -0.1  0.   0.1  0.2  0.  -0.2  0.   0.   0.8] 
方差描述占比: 0.04
第8的主成分为: [ 0.3  0.  -0.2 -0.2 -0.5  0.3 -0.6  0.2  0.2  0.2 -0.1 -0.   0.1] 
方差描述占比: 0.03
第9的主成分为: [-0.3  0.  -0.1  0.4  0.1  0.5 -0.4 -0.4 -0.2  0.1  0.2  0.1 -0.1] 
方差描述占比: 0.02
第10的主成分为: [ 0.1  0.5  0.1  0.1 -0.1  0.4  0.2  0.   0.1 -0.3 -0.  -0.6 -0. ] 
方差描述占比: 0.02
第11的主成分为: [-0.3 -0.3 -0.1 -0.4 -0.2 -0.1 -0.2 -0.4  0.1 -0.5  0.  -0.3 -0.1] 
方差描述占比: 0.02
第12的主成分为: [-0.4 -0.2 -0.2  0.2 -0.1 -0.3  0.   0.1  0.1  0.5 -0.  -0.6 -0.2] 
方差描述占比: 0.01
第13的主成分为: [-0.3  0.4  0.1 -0.2 -0.2 -0.1 -0.1 -0.1 -0.6  0.2 -0.5  0.1  0. ] 
方差描述占比: 0.01

代码

文本

特征向量里面的值表示该特征向量在原始数据空间的坐标轴上的投影,以及原始数据特征是如何通过线性组合构成其对应的特征。例如PC1的值为

$[- 0.1, 0.5, 0.2, - 0.0, - 0.3, - 0.2, 0.1, - 0.4, 0.5, 0.2, 0.2, 0.3, 0.0]$

从这组数中我们可以得到信息:第一主成分中不包含第4和第13个变量(他们的系数为0),相对地,有一些变量具有较大的权重,如第2个(0.5),和第9个(0.5).因此,我们可以通过特征向量来识别那些特征在这一主成分有更大的权重和贡献.

代码

文本

可以看出由上到下对数据分散性的描述比率逐渐减小至0.01.除此以外,只需要前五个特征向量的信息,就可以描述数据百分之八十的特征.

值得一提的是,PCA可以通过不同的角度理解,如投影、重构、可区分、旋转坐标系等.笔者选择了一个易于理解、拆分的角度来分步介绍.这里我们也提供一些优质的PCA相关科普,感兴趣的读者可以参考๐•ᴗ•๐:

算法理论02 主成分分析PCA: https://zhuanlan.zhihu.com/p/343182129 【机器学习】降维——PCA: https://zhuanlan.zhihu.com/p/77151308

代码

文本

如何通过主成分分析(PCA)分析分子轨迹数据?

场景一:分子结构变化

分子的运动轨迹可以看作是一个非常典型的高维数据场景.在分子动力学模拟中,分子内的每一个原子都被其在x,y,z三个方向上的坐标所表示.那么对于一个含N个原子的分子来说,每个原子都可以在x,y,z三个维度上移动,那么对于整个分子来说,它的总自由度(degree of freedom)为: $3 N$

对于化学场景来说,我们更关注分子的变化,那么这时我们可以将平移、转动这种并不会改变分子整体结构和能量的自由度(我们也称之为约束)去除,以下公式表示:

$F = 3 N - D$ 其中F表示自由度的数量，N表示原子数，D表示分子中的约束数。

因此,轨迹处理的第一步就是通过计算质心的位移和转动角动量来移除分子整体的平移和转动部分,从而只关注分子结构的变化.

对于非线性分子,我们需要扣除三个方向的平动和转动,因为他们并不会改变分子的内部结构(3N-6),。而对于线性分子,他们只有两个转动自由度的约束(3N-5).分子自由度的数量对于描述和理解分子的行为和性质非常重要.这里暗含一些分子信息的等变性与不变性,感兴趣的朋友一键直达BN*当我们说起神经网络的等变性，我们在谈论什么*

拿简单的乙醇分子( $C H_{3} C H_{2} O H$ )来说,虽然结构简单,但是它的总自由度为 $9 * 3 = 27$ ,扣除约束的自由度为 $9 * 3 - 6 = 21$ ,这意味着在分子的轨迹每一帧中(frame),这一样本有含有>20维信息.对于柔性大体系运动轨迹(如蛋白模拟),轨迹数据的信息量非常大.通过主成分分析,复杂的反应轨迹可以被降维,保留结构随时间变化的主要成分,并去除非关键原子的移动(也可想象为噪声),从而帮助研究人员更好的了解有机化学、生物化学等分子结构变化的和运动行为.

下面让我们实践一个简单反应的主成分分析过程——丙二醛的分子内氢转移过程(来源: Chem. Sci.,2019, 10, 9954)).

下图是轨迹的内禀反应坐标(intrinsic reaction coordinate,由福井谦一提出)——从过渡态(反应需要跨越的能垒结构)以固定步长沿梯度下降方向到达两侧反应物和产物的连续轨迹.

图中灰色的大球代表C原子,红色的大球代表O原子,而白色的小球代表H原子.

代码

文本

代码

文本

首先我们需要读入轨迹文件 malonaldehyde_IRC.xyz 分子轨迹xyz文件是一种常见的文件格式，用于存储和表示分子模拟或实验的分子结构和动力学轨迹数据。该文件以文本形式存储，通常使用.xyz作为文件扩展名。

分子轨迹xyz文件的基本结构如下：

第一行是一个整数，表示分子中原子的数量（N）。
第二行是一个注释行，可以包含有关该轨迹的额外信息，如模拟时间、温度等。
从第三行开始，每行包含一个原子的信息，按照特定的格式排列。每行包括四个字段：原子名称、原子的x坐标、原子的y坐标和原子的z坐标。

代码

文本

[10]

# 下载轨迹文件

! wget https://dp-public.oss-cn-beijing.aliyuncs.com/community/malonaldehyde_IRC.xyz

--2023-07-24 12:41:47--  https://dp-public.oss-cn-beijing.aliyuncs.com/community/malonaldehyde_IRC.xyz
Resolving ga.dp.tech (ga.dp.tech)... 10.255.254.37, 10.255.254.18, 10.255.254.7
Connecting to ga.dp.tech (ga.dp.tech)|10.255.254.37|:8118... connected.
Proxy request sent, awaiting response... 200 OK
Length: 13725 (13K) [chemical/x-xyz]
Saving to: ‘malonaldehyde_IRC.xyz.1’

malonaldehyde_IRC.x 100%[===================>]  13.40K  --.-KB/s    in 0.04s   

2023-07-24 12:41:47 (364 KB/s) - ‘malonaldehyde_IRC.xyz.1’ saved [13725/13725]

代码

文本

[11]

# 定义读取xyz轨迹的函数

def read_xyz_trajectory(file_path):

with open(file_path, 'r') as file:

frames = []

while True:

try:

num_atoms = int(file.readline()) # 第一行读入原子数量

next(file) # 跳过第二行注释行

coordinates = [] # 读取轨迹坐标

for _ in range(num_atoms): # 根据原子数量依次读取每一帧内的每一行的原子坐标

line = file.readline().split()

x, y, z = map(float, line[1:4])

coordinates.append([x, y, z]) # 将原子坐标储存至列表coordinate

frames.append(coordinates) # 将每一帧的原子坐标累积

except ValueError:

break

return np.array(frames) # 返回数组分子坐标信息

代码

文本

[12]

# 读取分子轨迹

frames1 = read_xyz_trajectory('malonaldehyde_IRC.xyz')

代码

文本

下面我们将使用sklearn的PCA功能对轨迹数据(xyz文件)进行主成分分析.注:如果你已有GROMACS或其他分子动力学package跑出的轨迹(包含拓扑信息,可被mdtraj读取,如h5文件),则可以直接调用python的mdtraj package丝滑PCA.考虑到本文的篇幅以及科普的重心为PCA及其在动力学轨迹中的代表场景,我们不会在本篇详细介绍这些package如何使用.为了让读者有更好的体验,我们将推出其他BN来实例化如何以Bohrium为平台,通过不同力场工具生成分子动力学轨迹并调用常见的python功能包来进行轨迹的数据分析. ๐•ᴗ•๐

代码

文本

[13]

# 载入sklearn的主成分分析功能

from sklearn.decomposition import PCA

flattened_trajectory1 = frames1.reshape(len(frames1), -1) # 将轨迹阵列展平为2D

pca = PCA(n_components=10) #指定要保留的主成分的数量

pca_result = pca.fit_transform(flattened_trajectory1) # PCA分析

# 打印前两个PC的解释方差比

print("第一主成分方差描述占比:", pca.explained_variance_ratio_[0],'\n')

print("第二主成分方差描述占比:", pca.explained_variance_ratio_[1],'\n')

# 提取PC并计算降维后的2D矩阵

principal_components = pca.components_

projected_data = pca_result

# 可视化降维后的轨迹

plt.scatter(pca_result[:, 0], pca_result[:, 1])

plt.title('Visualization of PCA')

plt.show()

# 画出累积方差解释图

plot_cumulative_eigenvalues(pca.explained_variance_ratio_)

第一主成分方差描述占比: 0.9392176170862856 

第二主成分方差描述占比: 0.05972972785437694

代码

文本

从图中我们可以看出,第一主成分（PC1）描述了93.9%的方差，而PC2占6.0%。由于这些成分捕获了反应过程中几何变化99%以上的总方差，因此我们的可以得到结论——重要的分子运动信息成功被这个二维子空间捕获(由于我们并没有祛除转动和平动的自由度,原来的空间根据总自由度的计算公式为 $3 * 9 = 27$ 维!)。为了更好的观察主成分所代表的原子运动,原文作者根据PC1和PC2特征向量重构分子的三维结构(PathReducer通过将PC转换回全维空间来生成分子几何的笛卡尔坐标，从而用PC重建结构,详情请点击原文链接),并将最大的两主成分根据当前帧和下一帧的变化,将原子运动方向投影回结构上,我们将会观察到这样的结果:

最重要的主成分（PC1）对应于H原子在两个O之间的运动以及两个C–C键的交替单键和双键特征。第二个最重要的主成分（PC2）主要对应于O的向内运动.因此,我们能够得知在H转移反应的过程中,H的位移为主体,约占93%,与此同时,两侧氧原子和氢原子的前后振动移动占比约6%,体现在左右两侧的氧原子先靠近,后远离的运动特征.同时我们也捕捉到了H原子在分子平面外的抛物线转移轨迹.

如果我们不使用PCA的主成分而是仅仅根据“经验主成分”——两侧O-H键的长短变化——来描述这一转移过程的话,我们会得到:

代码

文本

[14]

# 提取第一个O(第四个原子),第二个O(第五个原子),转移H(第九个原子)的坐标

positions_9 = frames1[:, 8] # 索引 8 对应原子9 (基于0开始的索引)

positions_5 = frames1[:, 4] # 索引 4 对应原子5

positions_4 = frames1[:, 3] # 索引 2 对应原子4

# 根据坐标计算每一帧 O4-H9 和 O5-H9 的键长

bond_lengths_9_5 = np.linalg.norm(positions_9 - positions_5, axis=1)

bond_lengths_9_4 = np.linalg.norm(positions_9 - positions_4, axis=1)

# 画出键长随轨迹变化的曲线

frame_numbers = np.arange(len(frames1)) # 提取轨迹长度

plt.scatter(bond_lengths_9_4, bond_lengths_9_5)

plt.axis("equal")

plt.xlabel('left O-H bond')

plt.ylabel('right O-H bond')

plt.title('Bond Lengths in the Trajectory')

plt.show()

代码

文本

通过上图我们只能阅读O-H键长的变化的过程,从而失去了其他相关的信息(如O-O的距离变化,H在平面外的移动特征).对于大分子体系,你可以把这个H想象为某个特定的残基(氨基酸单元)(residue)或残基片段,通过对轨迹的主成分分析,我们可以从复杂轨迹的结构变化中提取并分析它们的主要化学行为.另外,2D势能/自由能面的构建对于可视化反应过程有重要意义,因此可以通过主成分分析选择势能面坐标轴的表达形式.例如在GROMACS程序中,可以通过调用covar和sham模块来根据主成分绘制自由能面.

代码

文本

恭喜你!经过场景一你已经实现了对于简单分子结构变化轨迹的主成分分析,达成了“小试牛刀”的成就!

在下一个场景中,让我们一起level up,感受一个更加复杂,更特别,也更小众的化学场景

代码

文本

场景二:动力学效应

除了在反应轨迹、柔性大体系的分子轨迹中的应用外,主成分分析也适用于涉及动力学效应的有机反应轨迹的分析.

那么什么是 动力学效应(dynamic effect) 呢? 我们要先从传统过渡态理论谈起——

根据过渡态理论(Transition State Theory, TST,参考文献见附录),在化学反应进行过程中，反应物分子通过克服能垒的方式，经过过渡态形成新的化学键和解离旧的化学键，最终转变为产物。一般来说,过渡态结构代表单步或单位反应的结构变化.下图是一个二维的示意图: 而我们刚刚经历过的场景一就是一个典型的越过能垒,H从左侧传递到右侧的过程.

然而根据我们之前的介绍,分子的变化实际上是一个高维场景,三维势能面比二维势能线能更好地描述反应如何根据能量变化.

为了更好的理解过渡态理论和势能面,我们下面会通过两个函数来塑造“人工势能面”以直观的理解和感受它们.

代码

文本

[15]

# 传统过渡态模型势能面构造(大部分反应都遵循这一模型)

fig = plt.figure(figsize=(6,6))

# 创建三维画布

ax = fig.add_subplot(111, projection='3d')

# 定义X,Y和能量Z

x = np.linspace(0, 5, 100)

y = np.linspace(0, 5, 100)

X, Y = np.meshgrid(x, y)

Z = np.sin(X) + np.cos(Y)

# 绘图

ax.plot_surface(X, Y, Z, cmap='viridis')

# ax.axis('off')

# 设置X,Y,Z轴标签

ax.set_xlabel('X')

ax.set_ylabel('Y')

ax.set_zlabel('artificial Energy')

ax.set_title('Reaction PES')

plt.show()

代码

文本

在这个“人工势能面”中,我们定义了两个反应坐标X和Y, 和一个Z轴代表能量.沿着X从小到大的方向,分子从反应物到达一阶鞍点过渡态之后落入产物势阱.

然而对于一些特殊的反应,反应势能面可能并非这样简单,比如同一个过渡态可能会导向多个产物,再比如在原子经过过渡态后的动量使其在稳定前就已经越过之后的其他过渡态,又或者这两种效应同时存在.这种不能被传统过渡态理论解释的现象,被称为动力学效应(dynamic effect).

下面是一个具有后过渡态分叉(post-transition state bifurcation, PTSB,动力学效应的一种)性质的势能面: 当分子从左侧反应物势阱通过过渡态后,会进入较平坦的区域,之后随机落入两个产物势阱中.这种效应对于解释反应的选择性提供了新的可能,也为反应设计提出新的问题和挑战.比如PTSB可以介导酶催化等反应,也可以影响碳正离子重排反应的过程,为萜类化合物的合成提供新的视角.

代码

文本

[16]

# 后过渡态分叉势能面构造(少部分反应)

# 构造X,Y

x = np.linspace(-10, 10, 100)

y = np.linspace(-10, 10, 100)

X, Y = np.meshgrid(x, y)

# 根据X,Y计算势能Z

Z = (5e-8/16) * (X**2 - 4) + Y * (-1 - X) + Y**4 * X

# 绘图

fig = plt.figure(figsize=(6, 6))

ax = fig.add_subplot(111, projection='3d')

ax.plot_surface(-X, Y, Z, cmap='viridis')

# ax.axis('off')

# 设置X,Y,Z轴标签

ax.set_xlabel('X')

ax.set_ylabel('Y')

ax.set_zlabel('artificial Energy')

ax.set_title('PTSB Reaction PES')

plt.show()

代码

文本

图上的势能面两侧是完全对称的,也就是说如果只考虑势能面本身,从左侧经过过渡态进入势能面的分子落入两侧势阱的概率应各百分之五十.对于这类反应,如果只用一条动力学轨迹模拟来描述从反应物到某一产物的过程,那么另一产物的生成信息就被掩盖掉了.在这种情况下,只有反复从过渡态向两侧跑动力学轨迹才能够观察到分岔路径产生多于一种产物的现象.而这也是为什么类似的效应被冠以“动力学”之名——

多种产物之间的选择性不能通过对比过渡态的高低所决定,只有通过从同一过渡态多次反复收集反应的轨迹才能预测其不同产物的生成概率.

具有动力学效应的反应往往涉及到多个键的断裂与形成,比如下面这个反应的过渡态只有H5从C4转移至C1的特征,但当H位移后,部分轨迹通过C1-C4键(蓝色)的形成生成新的四元环,而其他轨迹则发生了C2-O3键(红色)断裂从而生成两个碎片 (来源:J. Am. Chem. Soc. 2022, 144, 17219−17231)

图中的反应物中的“冒号”处其实链接着一个金属催化剂,由于对反应影响不大,我们将其简化了.

代码

文本

由于涉及的反应原子众多,这类反应的势能面很难由特定的键长、键角、二面角、配位数等几何参数以二维或三维的形式直观地描述 —— 例如轨迹的分歧具体在哪个位置,是距离过渡态较远还是较近?分子运动的模式是更倾向于哪一侧产物?

这时候PCA就可以闪亮登场了!通过PCA我们可以提取轨迹的重要几何特征来帮助我们回答上面的问题.

以下的xyz文件中包含这一反应的九条动力学轨迹,其中有五条生成了蓝色产物P1,四条生成了红色产物P2.我们将对前五个原子(C1,C2,O3,C4,H5)的原子坐标进行主成分分析并投影轨迹.

代码

文本

[17]

!wget https://dp-public.oss-cn-beijing.aliyuncs.com/community/PTSB_trajs.xyz

--2023-07-24 12:41:49--  https://dp-public.oss-cn-beijing.aliyuncs.com/community/PTSB_trajs.xyz
Resolving ga.dp.tech (ga.dp.tech)... 10.255.254.7, 10.255.254.37, 10.255.254.18
Connecting to ga.dp.tech (ga.dp.tech)|10.255.254.7|:8118... connected.
Proxy request sent, awaiting response... 200 OK
Length: 2096255 (2.0M) [chemical/x-xyz]
Saving to: ‘PTSB_trajs.xyz.1’

PTSB_trajs.xyz.1    100%[===================>]   2.00M  --.-KB/s    in 0.09s   

2023-07-24 12:41:50 (22.9 MB/s) - ‘PTSB_trajs.xyz.1’ saved [2096255/2096255]

代码

文本

[18]

# 读取xyz轨迹

xyz_file = 'PTSB_trajs.xyz'

frames2 = read_xyz_trajectory(xyz_file)

# 提取1-5号原子的坐标

atom_indices = [0, 1, 2, 3, 4]

xyz_values = [[frame[i] for i in atom_indices] for frame in frames2]

coordinate_data = np.array(xyz_values)

# 将轨迹展平为二维

num_frames, num_atoms, _ = coordinate_data.shape

coordinate_data_reshaped = coordinate_data.reshape(num_frames, num_atoms * 3)

# PCA分析

pca = PCA(n_components=2) # 想要保留的主成分数目

principal_components = pca.fit_transform(coordinate_data_reshaped)

# 计算PC1和PC2的方差解释比率并打印

explained_variance_ratios = pca.explained_variance_ratio_

for i, ratio in enumerate(explained_variance_ratios):

print(f"方差解释比率 (PC{i+1}): {ratio:.4f}")

方差解释比率 (PC1): 0.3847
方差解释比率 (PC2): 0.2803

代码

文本

可以看出对于这种涉及多个键的形成与断裂的轨迹并像之前的H转移体系一样直观——前两个PC加起来也只能描述约66%的分子结构变化信息,这体现了轨迹的信息复杂性.下面让我们看一看轨迹们投影在PC1和PC2向量空间的结果:

代码

文本

[19]

#对轨迹文件进行处理,提取每一帧的时间信息(这里的内容并不重要,请放心大胆的跳过!)

def extract_runpoints(filename):

runpoints = []

with open(filename, 'r') as file:

for line in file:

if "runpoint" in line:

runpoint = int(line.split()[6]) # The integer after "runpoint" is in the 7th index of split line

runpoints.append(runpoint)

count_1 = 0

invert = False

result = []

for num in runpoints:

if num == 1:

count_1 += 1

if count_1 % 2 == 0:

invert = True

else:

invert = False

if invert:

result.append(-num)

else:

result.append(num)

return result

runpoints = extract_runpoints('PTSB_trajs.xyz')

代码

文本

[20]

# 将在PC1和PC2的向量空间投影的轨迹绘制出来

fig = plt.figure(figsize=(8, 6))

scatter = plt.scatter(principal_components[:, 0], principal_components[:, 1],c=runpoints,cmap="plasma")

plt.colorbar(scatter)

plt.xlabel('PC1')

plt.ylabel('PC2')

plt.title('Projection of Coordinate Data')

plt.show()

代码

文本

打个响指,把结构也加入到图中(为了让原子尽可能大,只可视化了1-5号原子): Untitled ACS Document 1996-1.png

代码

文本

从这张图上可以看出PCA处理后的结果可以清楚地区分两种不同产物的轨迹而保留它们从反应物到过渡态再到分岔点的相似性:

P1在投影后位于画布的右侧,P2位于画布的左上侧,而反应物位于画布的左下角.
两种轨迹在画布的中心有着明显的分岔点,并且分岔发生地较早,距离过渡态不远
因为反应物->过渡态->P1在图中处于一致的方向上,因此从原子运动的角度来看应倾向于生成P1

那么PCA的结果是否有局限性呢? 答案是:当然有局限性!

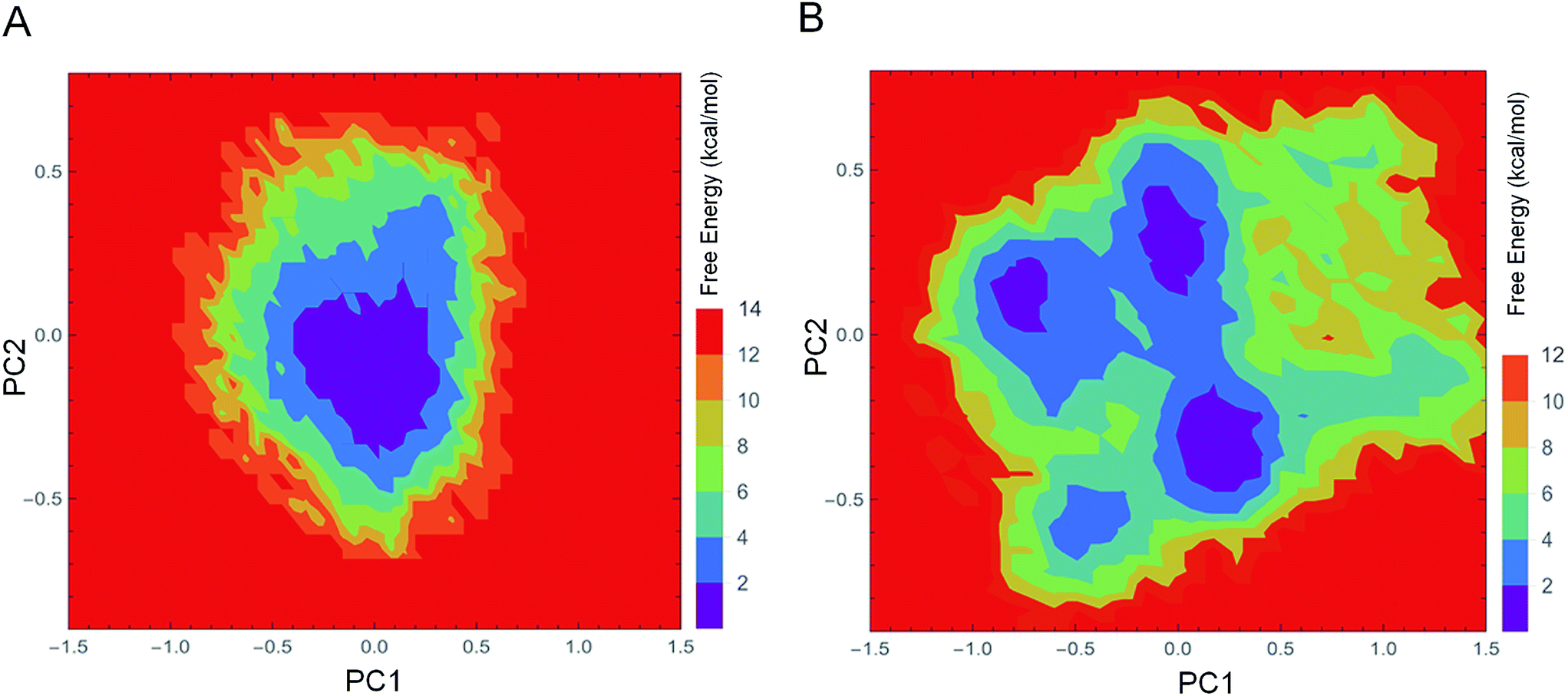
基于结构变化的投影结果只能体现原子运动方向的主要特征(原子的速度,动量,运动方向),并没有任何势能面形状的信息(比如:生成P1的通道斜率更大还是生成P2的通道斜率更大?).因此,在确认了PC后我们可以通过构建2D自由能势/能面的来可视化能量如何影响分岔效应.

恭喜你!你已经成功完成了场景二,在一个更复杂的反应机理下运用PCA提取轨迹的主要信息.这篇BN马上就要结束啦,让我们一起进入最后的部分吧.

代码

文本

结语

主成分分析(PCA)通过计算数据的协方差矩阵的特征向量来确定数据中最具信息量的方向以实现用于从高维数据中提取主要特征。在化学和生物学领域，动力学轨迹主成分分析用于识别和描述分子的主要运动模式和重要结构变化。比如——动力学轨迹PCA可以帮助揭示分子内部的协同运动、折叠和解折叠过程、重要域的大尺度运动等，从而为理解分子的功能和性质提供洞察和见解。主成分分析在构建势能面方面也具有一定的应用,帮助研究者选择合适的2D维度来可视化更多的信息。

需要注意的是，标准主成分分析以及基于标准主成分分析的降维方法们(如稀疏主成分分析spare PCA)具体的应用和结果取决于数据的质量、特征提取的方式以及拟合模型的选择和精度。因此，在具体的研究中，需根据实际情况综合考虑和优化PCA的应用方法。

回到开篇的例子,现在你不仅可以帮助百年前的东坡通过主成分分析来找到最好的观赏庐山的角度,还可以将PCA运用到酒水分析、分子动力学轨迹,甚至更多你感兴趣的场景中了!

代码

文本

附录

过渡态理论与过渡态搜索:

Truhlar, Donald G., Bruce C. Garrett, and Stephen J. Klippenstein. "Current status of transition-state theory." The Journal of physical chemistry 100.31 (1996): 12771-12800.https://doi.org/10.1021/jp953748q
Laidler, Keith J., and M. Christine King. "The development of transition-state theory." J. phys. Chem 87.15 (1983): 2657-2664.http://www.srneclab.cz/lectures/MC260P87/supp/lecture8b.pdf
Peng, Chunyang, and H. Bernhard Schlegel. "Combining synchronous transit and quasi‐newton methods to find transition states." Israel Journal of Chemistry 33.4 (1993): 449-454.https://onlinelibrary.wiley.com/doi/abs/10.1002/ijch.199300051
Weinan, E., Weiqing Ren, and Eric Vanden-Eijnden. "String method for the study of rare events." Physical Review B 66.5 (2002): 052301. https://doi.org/10.1103/PhysRevB.66.052301

内禀反应坐标:

Fukui, Kenichi. "The path of chemical reactions-the IRC approach." Accounts of chemical research 14.12 (1981): 363-368.http://dx.doi.org/10.1021/ar00072a001
Taketsugu, Tetsuya, and Mark S. Gordon. "Dynamic reaction path analysis based on an intrinsic reaction coordinate." The Journal of chemical physics 103.23 (1995): 10042-10049.https://doi.org/10.1063/1.470704

动力学效应:

Ussing, Bryson R., Chao Hang, and Daniel A. Singleton. "Dynamic effects on the periselectivity, rate, isotope effects, and mechanism of cycloadditions of ketenes with cyclopentadiene." Journal of the American Chemical Society 128.23 (2006): 7594-7607. https://doi.org/10.1021/ja0606024
Carpenter, Barry K. "Energy disposition in reactive intermediates." Chemical Reviews 113.9 (2013): 7265-7286. https://doi.org/10.1021/cr300511u
Jayee, Bhumika, and William L. Hase. "Nonstatistical reaction dynamics." Annual Review of Physical Chemistry 71 (2020): 289-313.https://doi.org/10.1146/annurev-physchem-112519-110208
Tantillo, Dean J. "Beyond transition state theory—Non-statistical dynamic effects for organic reactions." Advances in Physical Organic Chemistry. Vol. 55. Academic Press, 2021. 1-16.https://doi.org/10.1016/bs.apoc.2021.06.001

代码

文本

Scikit-Learn

pca

Molecular Dynamics

Tutorial

中文

notebook

Scikit-LearnpcaMolecular DynamicsTutorial中文notebook

已赞27

本文被以下合集收录

机器学习与DFT精华帖

gtang

更新于 2024-09-10

38 篇21 人关注

DeepMD

ytchen@szu.edu.cn

更新于 2024-09-04

10 篇14 人关注