问题背景

分子/材料体系的扩散系数、热导率、电导率等动力学性质，是分子动力学模拟计算的常见性质，也是针对电解质、有机溶液、半导体等实际问题研究时最常被关注的性质。在Bohrium案例广场搜索“扩散系数”，可以看到很多从理论、实战等各个方面的讲解。

但是，在实际应用的过程中、或者在分析具体问题的时候，忽略理论和数值计算的适用范围、知其然不知其所以然等，依旧是容易出现的问题。

本篇以扩散系数为例，介绍一些动手实战之前你需要知道的“讲究”。大致逻辑如下：

• 分子/材料体系扩散系数计算依托的理论基础：经典平衡态统计物理
• 理论适用条件：理论框架有哪些假设；“经典”啥时候不够用；“平衡态”啥时候不够用；
• 数值计算考虑：统计分布和时间关联具体怎么算；“热浴”的影响该怎么考虑？“尺寸效应”的影响该怎么考虑？“模型精度”的影响该怎么考虑？对Top-Down力场优化方法的考虑；
• 实际应用中的进一步近似处理：阿伦尼乌斯方程的应用；KMC的应用；粗粒化分子动力学的应用；

另外，本文希望起到的作用是称为一个需要考虑的潜在问题的导读索引，对于每个具体的问题，如果分诊确认，还需要更进一步的深入探究。

理论框架：内涵及适用条件

经典平衡态统计物理

这里推荐一篇非常优秀的notebook，统计力学中的含时过程。我们直接引用其中相关内容，更详细的讲解可以参考原文。

作为输运性质中最简单也最具代表性的，扩散系数的表达式可以直接通过应用Green-Kubo方程得到。这里热力学流是粒子流$J={\sum }_i{v}_i$，热力学力是粒子受到的恒定外力$F$，粒子流与外力成正比$J=(D/k_{B}T)F$，其中$D$即为扩散系数，代入Green-Kubo方程得到扩散系数的表达式

$$\begin{array}{c}D=\frac{1}{3N}{\int }_0^{\infty }⟨\sum _{i=1}^N{v}_i(0)\cdot \sum _{i=1}^N{v}_i(t)⟩\text{d}t\end{array}$$

粒子的速度分布服从麦克斯韦分布，不同粒子间彼此独立，因此

$$\begin{array}{c}D=\frac{1}{3N}\sum _{i=1}^N{\int }_0^{\infty }⟨v_i(0)\cdot v_i(t)⟩\text{d}t\end{array}$$

等式右侧是速度的自关联函数的积分，并对每个粒子求平均。然而在实际应用中，速度自关联函数的长时间收敛到0的速度很慢并且受到有限尺寸效应的影响，使得上式数值上难以使用。扩散系数还可以表达成爱因斯坦关系

$$\begin{array}{c}D=\frac{1}{6N}\sum _{i=1}^N\underset{t\to \infty }{\lim }\frac{\text{d}}{\text{d}t}⟨{\left|r_i(t)-r_i(0)\right|}^2⟩\end{array}$$

最初是由爱因斯坦在研究布朗运动时得到的，其中等式右侧使用的是粒子的均方位移（mean-square displacement，MSD）。上面扩散系数的两种形式的等价性很容易通过积分求导证明，但在实际模拟中使用爱因斯坦关系计算扩散系数数值上更稳定。已经有好几位小伙伴在案例广场上分享了扩散系数相关的工作，这一篇考察DMFF优化后的力场的表现，这一篇讨论数值计算MSD的细节，这一篇面向探究锂离子电池中的扩散现象。

理论框架的适用条件

在使用理论工具分析问题时，我们容易把理论当作“真理”。但每一个理论都有其适用条件，甚至即便一个问题在理论的适用范围内，进一步在计算机上的数值处理也很容易在很多地方出问题。往往在“闭着眼睛算一把”之前，我们需要知道采取的理论计算手段是否与实际需求相匹配。本部分和下一部分就将对此进行讨论。

我们讨论的对象是分子/材料体系，那么首先，在考虑具体问题时，相关自由度需要是原子/分子。这至少需要我们在两个方面进行额外注意。

• 第一，我们考虑的性质需要来自原子/分子的贡献。这对于扩散系数来说通常是成立的，但是对于其他性质，例如电导率来说，电子和离子均带电，所以电导率可能来自电子贡献或离子贡献。此外，一些宏观性质的微观贡献单元未必是唯一的，例如计算热导时“原子能量”给出的flux就不是唯一定义的，但宏观计算结果不受微观量定义的任意性而发生改变（但统计收敛性不同），这被称作相应性质的“规范不变性”。一个最直观的例子是，在计算分子扩散率时，只要不发生化学反应过程，那么通过追踪分子质心或通过追踪分子中任意原子得到的结果是一致的。但显然，当有质子迁移（proton transfer）的现象发生时，整个故事就不一样了。感兴趣更多的读者，我们推荐以下三篇读物：

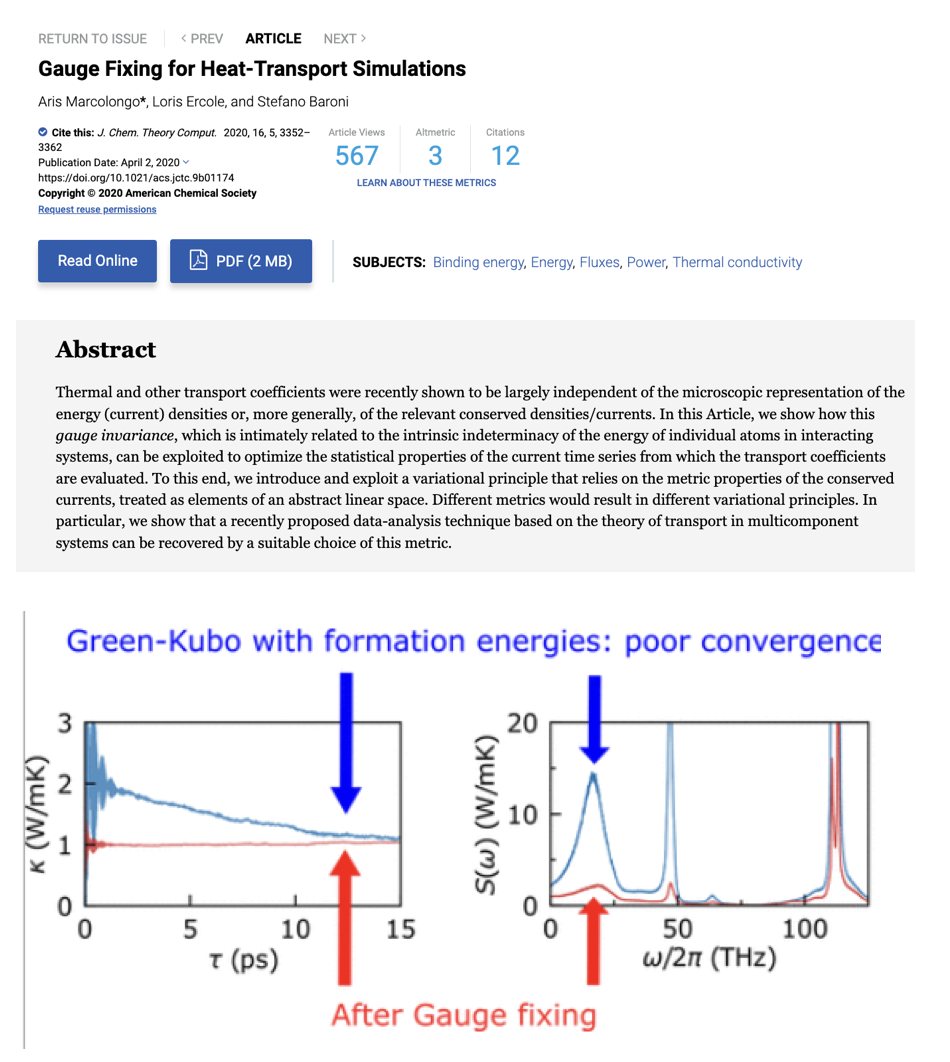
• 第二，更小或更大尺度的自由度能被有效地处理。这里，更小尺度的自由度通常指电子，在我们日常关注的温度压强范围下，电子效应通常可以被波恩-奥本海默近似有效处理，但极端情况未必；更大尺度的自由度指介观、宏观自由度，这通常以参数化的外场条件的形式（例如给定温度、压强、电压等）处理，但未必一定适用（例如在模拟燃烧爆炸等过程时，分子动力学中的常见控温手段是不适用的）。

进一步，既然我们用的是“经典平衡态统计物理”的框架，那么也要看“经典”何时被打破；以及“平衡态”何时被打破。在我们日常关注的温压范围内，对原子的经典近似是较为合理的。但是，对于像氢这样的轻元素、尤其在足够低温的时候，核量子效应会有很大的影响。处理静态、结构性质核量子效应的算法较为成熟，可以参考Hands-on PIMD | a quick guide on how to study nuclear quantum effects；但处理动力学性质核量子效应的数值算法并不成熟，感兴趣的同学可以参考这篇综述：Nuclear quantum effects enter the mainstream；对于“平衡态被打破”，这里希望提醒的是我们实际研究的对象是很容易面临这方面问题的（例如电池充放电过程）结合计算结果做分析的时候需要格外小心。

数值计算：值得关注的数值细节永远不嫌多

限定理论框架的适用范围已经让我们“戴着镣铐跳舞了”，而将理论翻译成数值计算要考虑的因素丝毫不少。当计算结果与预期不一致时，可能的误差来源往往可能非常多：

• 模型本身（力场形式和参数等）的误差；
• 数值设置带来的误差（积分格式、时间步长、计算精度设置等）；
• 统计误差（统计样本是否足够多、相互是否足够独立，等）；
• 边界条件（这里通常是周期性边界条件）和有限尺寸效应；

关于数值设置和统计误差

原则上，根据理论，我们要用以下公式做计算： $$\begin{array}{c}D=\frac{1}{3N}\sum _{i=1}^N{\int }_0^{\infty }⟨v_i(0)\cdot v_i(t)⟩\text{d}t\end{array}$$ 或者 $$\begin{array}{c}D=\frac{1}{6N}\sum _{i=1}^N\underset{t\to \infty }{\lim }\frac{\text{d}}{\text{d}t}⟨{\left|r_i(t)-r_i(0)\right|}^2⟩\end{array}$$

这里，$⟨...⟩$表示一个NVT/NPT统计分布的平均；时间从0到$t$则由微观的Hamiltonian Dynamics给出。

这篇notebook中给了一个数值计算过程的介绍：动力学性质计算与检验——以计算体系扩散性质为例，并给出了以下的计算方案：

在计算动力学性质时，我们通常需要进行NVE模拟，即微正则系综采样，而非NVT/NPT模拟。这是因为为恒温性与恒压性都可能会干扰体系的动力学特性，从而导致动力学性质预测产生偏差。因此，为预测体系在多温度梯度下的动力学特性，可以先对体系进行多段NVT模拟，并取平衡后的部分轨迹抽样进行NVE模拟，进而分析NVE轨迹得到体系动力学性质。这里推荐阅读Maginn E J等著 Best practices for computing transport properties 里面会有更详细的介绍。

在我们的体系中，给定温度下进行NVT模拟使其平衡，步长为1fs，每10000步即10ps记录一次，总模拟时长为2ns；取NVT轨迹后半段即1ns~2ns部分作为预平衡结构，抽取其中10帧结构进行NVE模拟，分析体系动力学特性并进行平均，同时减小误差。分子动力学模拟轨迹的各项操作可以通过 MDtraj 完成。

这可以被认为是一种方案。但是，这种方案中很多设置是需要格外小心的检查的。例如，“抽取其中10帧结构进行NVE模拟”，为什么是10帧？每帧结果一致的话，为什么需要那么多？如果每帧结果不一致的话，不一致是由每帧的“平衡能量”不一致带来的、还是每帧相应的NVE模拟的统计误差带来的？事实上，对于不同体系，上述问题的回答是很不一样的。我们需要做更多更加细致的分析及数值测试才能给出令人信服的答案。

当然，也会有更加直接的方案：直接进行某种NVT/NPT设置下的模拟，并对动力学性质进行计算。这在原则上的好处是足够长模拟时间下对统计分布的实现一定是符合需求的；但带来的问题是热浴对微观动力学的影响往往是不可忽略的。相关参考可见恒温分子模拟与热浴(NVT Ensemble and Thermostat)。一般来讲，往往热浴越强（通常通过模拟中effective damping time这一参数来调控）实现统计分布的效率越高、但热力学性质计算被破坏的程度也越高。 同时，不同类型热浴对不同类型热力学性质的影响也是不一样的。

既然从上述讨论中，我们看到很多方面都是“测了才知道”，那我们该如何测试呢？

对此，作者建议，对于一个不熟悉的新体系，条件允许的话，应该考虑做充分收敛的计算，然后再在兼顾效率和灵活性的考虑下，确定最佳方案。【这里希望给个完整的例子，但作者时间不够，有感兴趣的同学可以联系一起写一个。】

关于边界条件和有限尺寸效应

能模拟的粒子数不够、周期性边条件来凑。在进行分子动力学模拟时，我们只能对有限数量的粒子进行模拟。为了降低计算复杂度并减小边界效应，特别是在模拟固体、液体等凝聚态体系时，通常会采用周期性边界条件（Periodic Boundary Conditions，PBC）。周期性边界条件是一种处理模拟系统边界问题的方法，其核心思想是将研究对象（一个较小的原子或分子集合）视作无限大体系的重复单元。这意味着在三个正交的笛卡尔坐标轴（x，y，z）上，模拟系统在各个方向上都无限延伸，形成一个周期性排列的三维晶格。

当原子或分子穿越模拟盒子的边界时，周期性边界条件将其“包裹”回到系统的另一侧，使得系统中的原子或分子总数保持恒定。这种处理方法的优点在于它可以模拟出更接近无限体系的性质，同时还能保持计算规模在可承受的范围内。

边界条件和有限尺寸效应对不同性质的计算影响程度是非常不同的。很多局部结构相关的性质只要模拟的体系够大、可能基本不受影响；像径向关联函数这样的性质可以随着模拟体系的增大很快收敛；但也有一些性质压根不能指望通过体系往大算来收敛，其中最有代表性的便是固体物理学中极化体系的纵横光学声子分裂（LO-TO splitting）现象。

对扩散系数等动力学性质来说，边界条件和有限尺寸效应的影响同样不能忽略。一个经典的描述自扩散系数$D$随着模拟的盒子尺寸$L$的关系被称为Yeh–Hummer (YH) correction： $$D(\infty )=D(L)+\frac{k_{B}Tϵ}{6\pi \eta L}$$ 这里$D(\infty )$指盒子无限大、即理想的真实体系的扩散系数，$\eta$指剪切黏度(同样可以由分子动力学模拟算出来)，$k_B$指玻尔兹曼常数，$T$指绝对温度，而$ϵ$是一个无量纲数，对于周期性立方晶格来说取值为2.837298。

有限体系由于周期性边条件的限制，容易低估扩散系数；由YH公式可以看出，被低估的程度受到模拟的体系大小$L$和剪切黏度$\eta$的影响，并可以做渐进的修正。事实上，我们经常会在有限尺寸效应相关的讨论里看到类似下图这样的呈现形式：

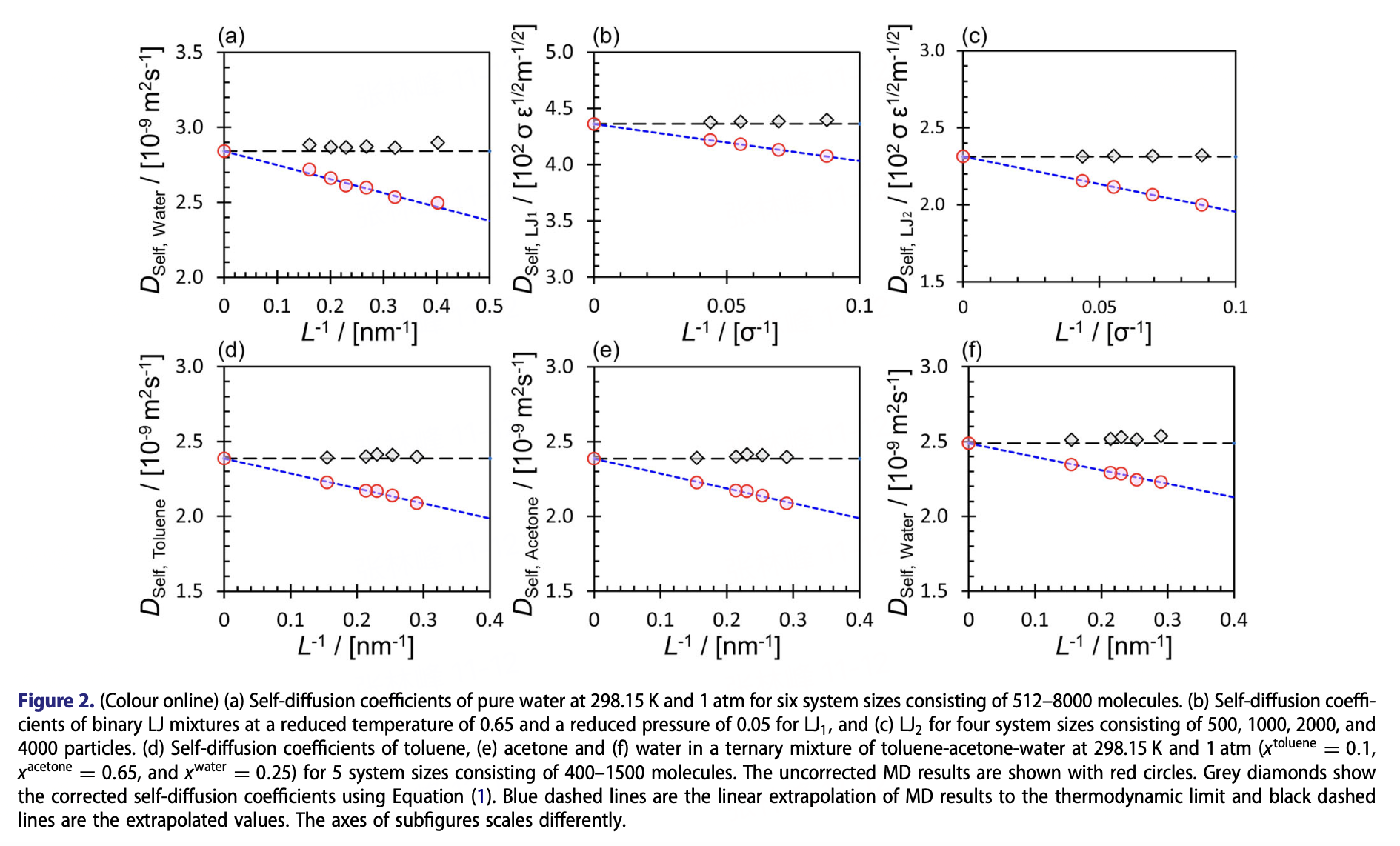
感兴趣的读者可以通过这个图背后的这篇综述进一步了解：

最后，这篇Bohrium Notebook（使用深度势能分子动力学进行固态电解质研究实战）详细介绍了固态电解质扩散系数相关的计算。事实上，对于感兴趣更多的读者，我们也非常推荐下面这篇文章。

关于模型参数

最后，在一切理论框架、数值方法等因素被充分探究过后，最终影响整体结果的便是我们使用的相互作用模型了，这里特指描述原子间相互作用的力场模型。值得一提的是，Bottom-Up出发的力场模型自然是满足第一性原理精度的程度越高越好，但同时也要全面地考虑截止到目前为止介绍的所有因素；但Top-Down出发的力场可能是未必的，其参数形式本身可能是为了更好地匹配实验结果，那么大致的体系大小、动力学方程、核量子效应的考虑等都可能会隐式地被参数化形式包含，粗粒化体系的考虑可能更是如此。感兴趣的读者可以参考这里的一个初步的讨论。

关于实际应用中的进一步近似处理：

有了上述的介绍，我们希望大致介绍清楚一个具体性质计算背后问题方方面面的考虑因素。事实上，Bohrium Notebook上关于这个话题的介绍还远不止这些。例如，这篇探讨了扩散系数与阿伦尼乌斯方程应用，这篇介绍了机器学习辅助蒙特卡洛模拟计算扩散系数，一些粗粒化模型也希望能最大程度地做准动力学性质。这些处理背后都有进一步的近似。如果这些近似能被很好地满足，那么我们就容易更快更好地得到结果；如果不能，那么很多时候结果不对未见得完全是计算不靠谱，可能是处理方式和适用条件不合适。总而言之，这需要我们对要算的性质形成较为系统的认识和较为丰富的经验。