Part1:DFT算法介绍
密度泛函理论(Density Functional Theory,简称DFT)是一种用于计算原子、分子和固体电子结构的理论方法。它基于量子力学原理,通过求解电子的波函数来描述系统的性质。DFT是化学和物理领域中最常用的计算方法之一,因为它在预测分子结构、反应性和性质方面表现出色。
基本原理 DFT的基本原理可以追溯到Thomas-Fermi模型和Hohenberg-Kohn定理。Hohenberg-Kohn定理指出,一个给定系统的基态电子密度唯一地决定了系统的全部基态性质。Kohn-Sham方程则提供了解决这个问题的框架,它把原先的多体问题转化为一个单体问题,通过引入一个虚拟体系中的非相互作用电子的动能与交换-相关势来模拟真实系统中电子的行为。
Kohn-Sham方程 Kohn-Sham方程的基本形式如下:
其中是Kohn-Sham哈密顿算符,是Kohn-Sham波函数, 是外势,包括原子核引力和外加电场, 是哈特里势,描述了电子间的库仑排斥作用, (r) 是交换-相关势,包括交换和相关能的贡献, 是Kohn-Sham波函数的能量本征值。
密度与势
通过Kohn-Sham波函数构造电子密度:
而交换-相关势可以通过密度泛函的近似来确定。常用的密度泛函包括局域密度近似(LDA)和广义梯度近似(GGA)等。这些近似的目标是尽可能准确地描述电子系统的交换和相关能。
数值实现 实际计算中,DFT需要进行数值积分和优化。常用的数值方法包括基组展开法、平面波展开法和格点方法等。此外,DFT计算还需要考虑周期性边界条件(对于固体系统)、自洽场迭代和收敛性等问题。
应用 DFT在材料科学、化学反应动力学、表面科学等领域有着广泛的应用。它可以用来研究分子的构型、反应活性、电子结构和能带特性等重要性质。
结语 密度泛函理论为研究原子和分子的电子结构提供了强大的工具。尽管DFT的一些近似可能限制了其精度,但它仍然是一种非常有用的方法,可以提供对系统性质的定性和定量理解。
Part2: Li元素的相关介绍
锂是一种轻金属元素,其发现和研究历史悠久而丰富。它的发现可以追溯到 19 世纪初,当时瑞典化学家约翰·奥古斯特·阿尔弗雷德·阿雷尼乌斯·阿尔法得知锂的存在,并通过电解锂氯化物从锂的氧化物中分离出来。
锂在自然界中相对较稀有,主要以矿物的形式存在,如锂辉石和云母。它的物理化学性质使其在许多领域有广泛的应用。首先,锂是一种非常轻的金属,密度较低,但具有较高的熔点和沸点。由于其低密度和良好的电导率,锂被广泛用于制造轻型合金,特别是在航空航天和汽车工业中。此外,锂还具有在电池中储存和释放能量的能力,因此被广泛用于电池制造,如锂离子电池和锂聚合物电池。
锂还可形成许多化合物,包括锂氢化物、锂碳酸盐和锂氟化物等。其中,锂氢化物是一种重要的化合物,可用作氢气的储存和运输介质,有望在清洁能源领域发挥重要作用。此外锂的化合物还被广泛用于医药、陶瓷和玻璃工业。
随着电动汽车和可再生能源的兴起,对锂的需求正在不断增加。因此,锂的开采和利用成为了当今重要的经济活动之一。同时,锂资源的保护和可持续利用也成为了全球范围内的关注焦点,以确保能源安全和环境可持续发展。
Part3:锂元素基态结构的研究
进行cell-relax计算,相关的输入如下所示:
INPUT:
INPUT_PARAMETERS suffix Li ntype 1 nelec 0.0 pseudo_dir ./PP_ORB orbital_dir ./PP_ORB ecutwfc 100 # Rydberg scf_thr 1e-6 # Rydberg basis_type lcao calculation cell-relax # this is the key parameter telling abacus to do a optimization calculation force_thr_ev 0.01 # the threshold of the force convergence, in unit of eV/Angstrom stress_thr 2 # the threshold of the stress convergence, in unit of kBar relax_nmax 100 # the maximal number of ionic iteration steps out_stru 1
STRU:
KPT
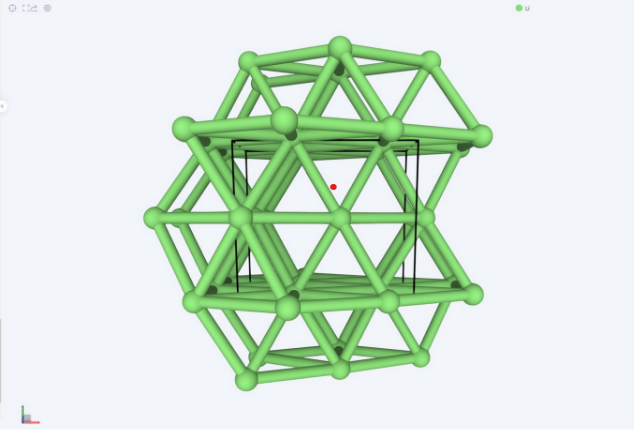
最后得出结果为Li的基态结构是体心立方结构,如下图所示
Part4: Li元素的收敛性测试
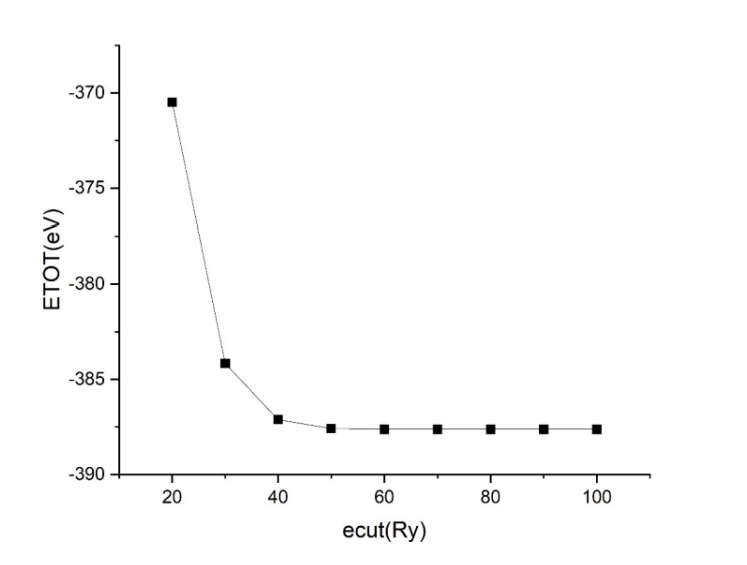
平面波收敛性测试: INPUT 文件中设置 ecut 分别为 20-100,间隔为 10,其余不变。 STRU 文件中按照附加题中 cell-relax 得出的结果设置结构。 KPT 文件中 K 点个数设置为 444。随后可利用脚本提取数次结果最后的基态能量 最后得到的结果如图 1 所示,可见当 ecut≥50 时,即可认为结果收敛。 具体的输入文件见数据集,这里不作展示。
Kpoint收敛性测试:
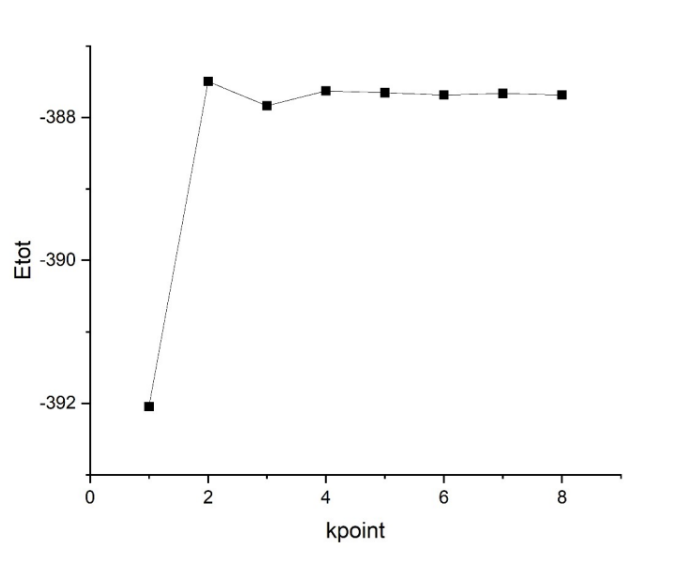
INPUT 文件中设置 ecut 分别为 100 。 STRU 文件中按照附加题中 cell-relax 得出的结果设置结构。 KPT 文件中 K 点个数设置为 111-888,其余不变。 最后得到结果如图 2 所示,可见当 k 点个数≥444 时,即可认为收敛。
上述步骤均用脚本完成,这里展示ecut中的脚本作为示例。利用这一脚本即可完成输入文件的设置与计算,后续利用grep提取每个文件夹中的ETOT即可。
#!/bin/bash
for ((i=20; i<=100; i+=10)); do
INPUT="
#Parameters (1.General) b
INPUT_PARAMETERS
suffix Li
calculation scf
symmetry 1
pseudo_dir ./PP_ORB
orbital_dir ./PP_ORB
basis_type pw
ecutwfc $i
#Parameters (2. SCF iterations)
scf_nmax 100
scf_thr 1e-8
#Parameters (3. Solve KS equation)
nbands 10
ks_solver cg
#Parameters (4.Smearing)
smearing_method gauss
smearing_sigma 0.01
"
KPT="
K_POINTS
0
Gamma
4 4 4 0 0 0
"
STRU="
ATOMIC_SPECIES
Li 6.941 Li_ONCV_PBE-1.0.upf
NUMERICAL_ORBITAL
Li_gga_7au_100Ry_4s1p.orb
LATTICE_CONSTANT
1.8897261258369282
LATTICE_VECTORS
3.43935 0.0000000000 0.0000000000
0.0000000000 3.43935 0.0000000000
0.0000000000 0.0000000000 3.43935
ATOMIC_POSITIONS
Direct #Cartesian(Unit is LATTICE_CONSTANT)
Li #Name of element
0.0 #Magnetic for this element.
2 #Number of atoms
0 0 0 1 1 1 Li
0.5 0.5 0.5 1 1 1 Li
"
job='
{
"job_name" : "hw2_Li_ecut'$i'",
"command" : "OMP_NUM_THREADS=1 mpirun -n 2 abacus",
"log_file" : "OSZICAR",
"backward_files" : [],
"project_id" : 15069,
"platform" : "ali",
"job_type" : "container",
"machine_type" : "c2_m4_cpu",
"image_address" : "registry.dp.tech/dptech/abacus:3.6.1"
}
'
mkdir -p "ecut$i"
echo "$INPUT" > "ecut$i/INPUT"
echo "$KPT" > "ecut$i/KPT"
echo "$STRU" > "ecut$i/STRU"
echo "$job" > "ecut$i/job.json"
cp -r PP_ORB "ecut$i"
done
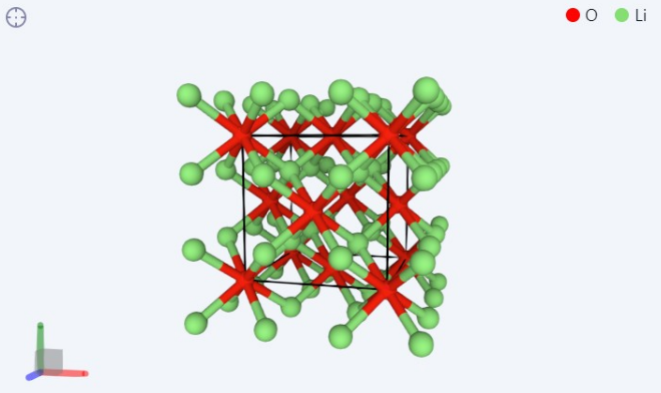
Part5. Li的简单化合物的结构弛豫计算
这里选取的简单氧化物为氧化锂LiO, 查找资料发现 LiO 这一常见化合物的基态结构是反萤石结构。将这种结构作为 STRU 的 输入文件,运行 cell-relax 计算,可以得到最后结构如图所示,即晶格常数为 4.716A 的反萤石结构。由于这一步是用lbg提交,故数据集中并没有相应的OUT文件。