新建
快速上手1D Hindered Rotor(1DHR)方法 | 采用1DHR方法计算丙基苯(n-propylbenzene)扭转非简谐因子
Astartes
推荐镜像 :Basic Image:ubuntu22.04-py3.10
推荐机型 :c2_m4_cpu
赞 2
目录
数据集
1DHR-tutorial(v5)
快速上手1D Hindered Rotor(1DHR)方法 | 采用1DHR方法计算乙烷(ethane)扭转非简谐因子
代码
文本
©️ Copyright 2023 @ Vincent Chen
日期：2023-09-28
共享协议：本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。
请引用文献：W. Chen, P. Zhang, D. G. Truhlar, J. Zheng and X. Xu, J. Chem. Theory Comput., 2022, 18, 7671–7682. https://doi.org/10.1021/acs.jctc.2c00952
代码
文本
本项目旨在帮助大家了解用于修正气相分子热力学参数计算中扭转非简谐问题的一维受阻转子方法。项目以乙烷为例，手把手教大家使用Fourier Grid Hamiltonian (FGH)方法求解一维扭转势能面上的薛定谔方程，从而计算相应扭转运动的非简谐配分函数来替代原本的简谐运动配分函数。
---代码
文本
代码
文本
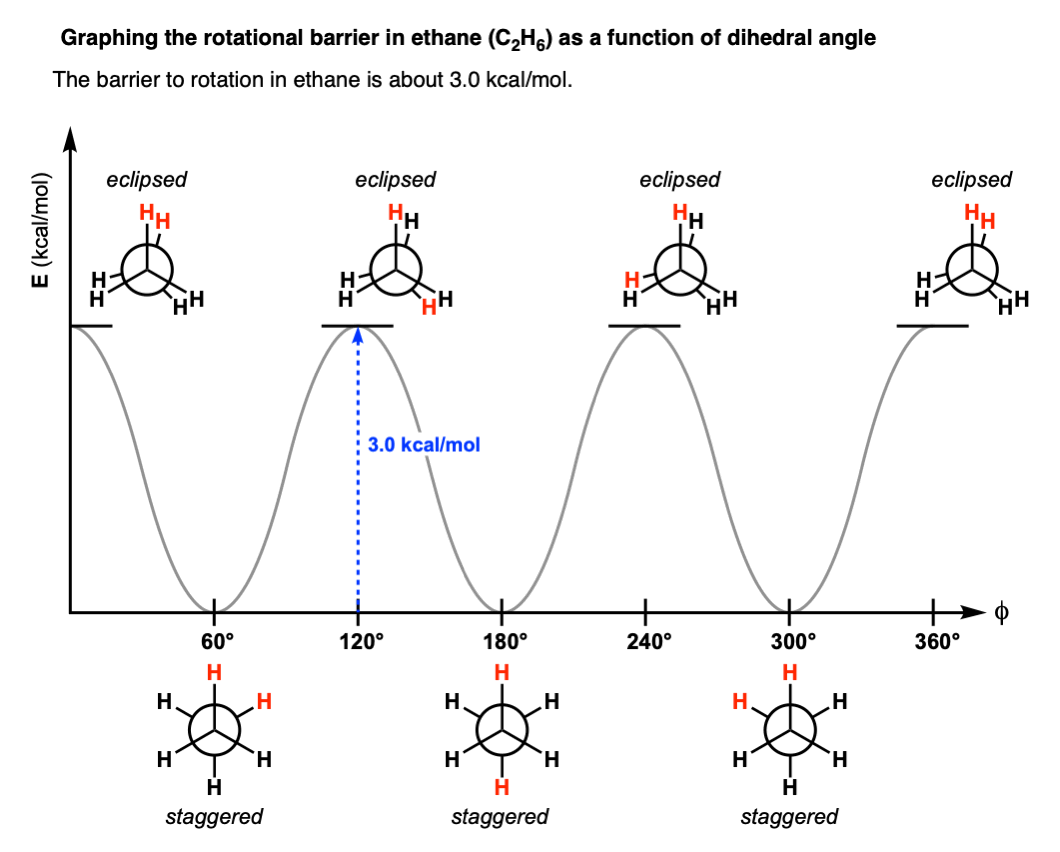
Ref：https://www.masterorganicchemistry.com/2020/02/28/staggered-vs-eclipsed-conformations-of-ethane/
气相分子的热力学参数是化学反应研究与工程建模上不可或缺的重要参数。除了实验方法与Benson等人提出的Group additivity方法外，我们还能基于量子化学的计算结果，从统计力学角度计算热力学参数。现今最广泛应用于热力学参数计算的统计模型是刚性转子-简谐振子(RRHO)模型，顾名思义，这种模型将分子的三个转动自由度采用刚性转子模型处理，而3N-6/3N-5个振动自由度采用简谐振子模型处理。
正如上面所说，RRHO模型采用简谐振子模型来处理分子内部的振动自由度。这种模型对于柔性分子（即分子中含有多个可旋转单键的分子，比如长链烷烃）的低频振动模态而言不再适用：
- 我们可以观察到低频扭转模态基本上描述的是分子内部存在于单个/多个键轴的转动。从一维（即分子内部绕单个键轴扭转）的角度来看，这种分子内转动(internal rotation/torsion)的势垒为有限势垒的周期势，与简谐振子模型的二次势差异较大。
- 同时，由于频率较小，这种低频模式对于配分函数的影响是很大的。这种影响会导致我们计算得到的热力学参数与反应速率常数的误差（热力学参数误差见图1 Gao et al. ，熵可达4-6 cal/mol/K；动力学参数误差见图2 Seal et al. 速率常数可达几个数量级）。
而非简谐因子，作为非简谐处理下扭转运动配分函数同简谐处理下该运动配分函数的比值，可以一定程度上描述该分子的柔性程度，并且直接与计算的热/动力学量偏差有关。现有的气相分子低频扭转矫正方法中，用得比较广的有两种：一维受阻转子方法(1D-HR)与多结构扭转非简谐(MS-T)方法。这里我们介绍第一种1D-HR方法。
1D-HR方法的计算流程主要可分为三个部分：
- 从简正模态分析(normal mode analysis)得到的简谐频率中分离扭转成分，并获取围绕单键扭转运动的约化转动惯量；
- 扫描一维扭转势能面，利用FGH方法计算一维薛定谔方程，获取扭转运动能级；
- 计算扭转运动非简谐配分函数，求取非简谐因子(非简谐配分函数与扭转成分对应的简谐配分函数的比值）。
本案例中的计算均用到了数据集中的计算结果与代码文件，我在这里做简要介绍：
FGH_Util文件夹下为本Notebook用到的Fourier Grid Hamiltonian算法代码文件；ethane文件夹下包含运用Gaussian软件计算得到的乙烷的结构，投影频率以及一维扭转势能面的log输出文件；
代码
文本
[2]
! pip install scipy matplotlib
Looking in indexes: https://pypi.tuna.tsinghua.edu.cn/simple Requirement already satisfied: scipy in /opt/mamba/lib/python3.10/site-packages (1.10.1) Requirement already satisfied: matplotlib in /opt/mamba/lib/python3.10/site-packages (3.8.0) Requirement already satisfied: numpy<1.27.0,>=1.19.5 in /opt/mamba/lib/python3.10/site-packages (from scipy) (1.24.2) Requirement already satisfied: cycler>=0.10 in /opt/mamba/lib/python3.10/site-packages (from matplotlib) (0.11.0) Requirement already satisfied: contourpy>=1.0.1 in /opt/mamba/lib/python3.10/site-packages (from matplotlib) (1.1.1) Requirement already satisfied: fonttools>=4.22.0 in /opt/mamba/lib/python3.10/site-packages (from matplotlib) (4.42.1) Requirement already satisfied: python-dateutil>=2.7 in /opt/mamba/lib/python3.10/site-packages (from matplotlib) (2.8.2) Requirement already satisfied: kiwisolver>=1.0.1 in /opt/mamba/lib/python3.10/site-packages (from matplotlib) (1.4.5) Requirement already satisfied: packaging>=20.0 in /opt/mamba/lib/python3.10/site-packages (from matplotlib) (23.0) Requirement already satisfied: pillow>=6.2.0 in /opt/mamba/lib/python3.10/site-packages (from matplotlib) (10.0.1) Requirement already satisfied: pyparsing>=2.3.1 in /opt/mamba/lib/python3.10/site-packages (from matplotlib) (3.1.1) Requirement already satisfied: six>=1.5 in /opt/mamba/lib/python3.10/site-packages (from python-dateutil>=2.7->matplotlib) (1.16.0) WARNING: Running pip as the 'root' user can result in broken permissions and conflicting behaviour with the system package manager. It is recommended to use a virtual environment instead: https://pip.pypa.io/warnings/venv
代码
文本
[3]
%matplotlib inline
import numpy as np
import scipy
import matplotlib.pyplot as plt
from scipy.interpolate import CubicSpline
from scipy.optimize import curve_fit
import sys
sys.path.insert(0, '/bohr/1DHR-tutorial-bho9/v5/FGH_Util/')
import FghUtility ## 文件中包含编写的FGH求解器与配分函数计算器
代码
文本
3.1.1 优化结构
要计算乙烷的简谐频率，我们需要先先优化乙烷分子的几何结构，相关Gaussian输入如下（文件中同时优化乙烷分子结构，并计算简谐振动频率）：
代码
文本
[1]
! cat /bohr/1DHR-tutorial-bho9/v5/ethane/geom.com
%nproc=24 # opt=(calcall) nosym freq=NORAMAN m062x/def2tzvp integral=ultrafine ethane 0 1 C 2.35487092 -0.46376828 0.03082697 H 2.71152452 -1.47257858 0.03082722 H 2.71154447 0.04062984 -0.84282428 H 1.28487092 -0.46375441 0.03082655 C 2.86821316 0.26218817 1.28823183 H 3.93821316 0.26217430 1.28823226 H 2.51155957 1.27099846 1.28823158 H 2.51153961 -0.24220996 2.16188308
代码
文本
代码
文本
[2]
! cat /bohr/1DHR-tutorial-bho9/v5/ethane/hindered.com
%nproc=24 # freq=(hinderedrotor) m062x/def2tzvp integral=ultrafine ethane 0 1 C 2.357636000000 -0.459874000000 0.037581000000 H 2.705018000000 -1.492999000000 0.008370000000 H 2.705010000000 0.031385000000 -0.871747000000 H 1.267795000000 -0.476690000000 0.008383000000 C 2.865448000000 0.258294000000 1.281478000000 H 3.955289000000 0.275110000000 1.310676000000 H 2.518066000000 1.291419000000 1.310689000000 H 2.518074000000 -0.232965000000 2.190806000000
代码
文本
[ ]
from dpdispatcher import Machine, Resources, Task, Submission
machine0 = Machine(
batch_type = "Slurm",
context_type= "SSHContext",
local_root = "/bohr/1DHR-tutorial-bho9/v5/ethane/",
remote_root = "/home/user123/dpdispatcher_work_dir/", # 请修改此处
remote_profile={
hostname: "39.106.xx.xxx", # 请修改此处
username: "user123", # 请修改此处
password: "", # 请修改此处
port: 22,
timeout: 10
}
)
resources0 = Resources(
number_node=1,
cpu_per_node=24,
queue_name="", # 请修改此处
custom_flags=["#SBATCH --nice=100", "#SBATCH --time=24:00:00"],
)
task0 = Task(
command="g16 RelaxedScan.com",
task_work_path="RelaxedScan/", # 请修改此处
forward_files=["RelaxedScan.com"],
backward_files=["RelaxedScan.log"],
outlog="out.txt",
)
sub0 = Submission(work_base="/bohr/1DHR-tutorial-bho9/v5/ethane/",\
machine = machine0, resources = resources0, \
task_list = [task0])
sub0.run_submission()
代码
文本
3.3 计算结果后处理
这里我们向大家介绍如何从hinderedrotor计算结果中获取扭转频率及约化转动惯量。我们需要在计算结果中以reduced moment of inertia为关键词搜寻并打印相应内容：
（然而，我们建议采用Kilpatrick and Pitzer人的方法更严格的获得约化转动惯量，这个方法在MSTor 2023软件中被实现。）
代码
文本
[6]
! grep -A 5 "reduced moment of inertia" /bohr/1DHR-tutorial-bho9/v5/ethane/hindered.log
frequencies (cm**-1), reduced moment of inertia (amu*Bohr**2)
1
Frequencies --- 308.5388
Reduced Moments --- 0.6195
Bond
1 - 5 1.0000
代码
文本
这里展示的是reduced moment of inertia关键词后的几行内容。这里展示的是1号扭转运动：该扭转运动的扭转频率为：308.5388cm**(-1)，约化转动惯量为：0.6195 amu*Bohr**2，它对应的扭转键为Bond：1-5，即乙烷的C-C单键。需要注意的是，对于复杂分子，在扭转识别中，这个扭转成分可能不到1，我们一般选择成分最大的扭转键对应即可。
代码
文本
[7]
! cat /bohr/1DHR-tutorial-bho9/v5/ethane/RelaxedScan.com
%nproc=24 # opt=(modredundant,noeigentest) nosym m062x/def2tzvp integral=ultrafine ethane 0 1 C 2.357636000000 -0.459874000000 0.037581000000 H 2.705018000000 -1.492999000000 0.008370000000 H 2.705010000000 0.031385000000 -0.871747000000 H 1.267795000000 -0.476690000000 0.008383000000 C 2.865448000000 0.258294000000 1.281478000000 H 3.955289000000 0.275110000000 1.310676000000 H 2.518066000000 1.291419000000 1.310689000000 H 2.518074000000 -0.232965000000 2.190806000000 2 1 5 6 S 36 10.
代码
文本
从计算输出结果中将扫描得到的势能面提取出来：
代码
文本
[12]
# 势能面获取
Pot = ! grep -A 10 "\\HF=" /bohr/1DHR-tutorial-bho9/v5/ethane/RelaxedScan.log | tr "\n" " " | sed 's/ //g' |sed 's/$/\n/'|sed 's/.*HF=//g'|sed 's/\\RMSD=.*//g'
Pot = [ float(i) for i in Pot[0].split(',') ][:-1]
Pot = np.array(Pot) - min(np.array(Pot))
# 扭转角获取
Dihe = ! grep 'D(2,1,5,6)' /bohr/1DHR-tutorial-bho9/v5/ethane/RelaxedScan.log |awk '{print $4}'|tail -n +2
Dihe = [ float(i) for i in Dihe ][:-1]
# 数据组合与重排
Data = np.array(list(zip(Dihe,Pot)))
Data = np.array(sorted(Data, key=lambda x: x[0]))
temp = Data[0,:].copy() # 需要保证最后一个点与第一个点一致
temp[0] += 360.0
Data = np.vstack((Data,temp))
plt.plot(Data[:,0],Data[:,1])
# 采用scipy library，拟合数据点至周期函数
x, y = Data[:,0]*2*np.pi/360.0, Data[:,1]*2.194746E5
# cubic spline interpolation, need x increase monotonically, periodic: y[-1] == y[0]
f = CubicSpline(x, y, bc_type='periodic') # for periodic potential
代码
文本
4.2 采用FGH方法求解一维扭转运动的薛定谔方程
描述一维扭转运动的薛定谔方程如下表示：（ref：Pfaendtner et al.)
其中i表示第i个扭转；j为计算得到的第i个扭转的能级j；为该扭转的约化转动惯量；为该扭转的symmetry number，例如：甲基为3；为能级j的简并度，对于一维势能面而言，能级简并度始终为1。
代码
文本
[27]
# 扭转的约化转动惯量 (amu*Ang**2)，为3.1.2节中得到的约化转动惯量的变换
Ang2au = 1.889726 # 常数
MomInert = 0.6195*Ang2au*Ang2au
# Rotational Top的内部对称数/每个扭转的对称数
sigma = 3
# 采用FGH方法计算扭转能级
au2cm = 5.291772E-9
FghUtility.FGH_method(True, f, 257, mass=MomInert, xMax=np.max(x), xMin=np.min(x))[0]*au2cm
代码
文本
图中的虚线所代表的是薛定谔方程求解得到的一维扭转运动的能级。
代码
文本
[28]
# 定义温度（单位：K）
temp = [213,225,250,298.15,300,325,350,375,400,425,450,475,500,550,600,650,700,800,1000,1200,1400,1600,1800,2000,2200,2300,2400,2500,2600,2700,2800,2900,3000]
# 计算配分函数（无单位）
AnhPart = []
energies = FghUtility.FGH_method(True, f, 257, mass=MomInert, xMax=np.max(x), xMin=np.min(x))[0]
for T in temp:
AnhPart.append(FghUtility.get_part(energies, T, sigma=sigma))
AnhPart = np.array(AnhPart)
代码
文本
[29]
# 输入3.1.2节中得到的扭转频率（cm-1）
HarmVibFreq = 308.5388
HarmVibFreq = np.array([HarmVibFreq])
# 计算相应的简谐配分函数
HarmVibPart = FghUtility.vib_part(HarmVibFreq, temps=temp)[1]
代码
文本
[30]
F_anh = AnhPart / HarmVibPart
print(F_anh)
[1.4518005 1.44547176 1.43700105 1.43213103 1.43214133 1.43321257 1.43557494 1.43873119 1.44232548 1.44610184 1.44987644 1.4535183 1.45693565 1.46286819 1.46740326 1.4704724 1.47211714 1.47155121 1.45854864 1.43558835 1.40753143 1.37725986 1.3464217 1.31593995 1.28631522 1.27191004 1.25780122 1.24399861 1.23050693 1.21732703 1.20445686 1.19189217 1.17962712]
代码
文本
参考
- 请引用文献：W. Chen, P. Zhang, D. G. Truhlar, J. Zheng and X. Xu, J. Chem. Theory Comput., 2022, 18, 7671–7682. https://doi.org/10.1021/acs.jctc.2c00952
代码
文本
已赞2
推荐阅读
公开
Hackthon | Gromacs分子动力学结构数据的2D表示
拉莫进洞
发布于 2023-08-08
1 赞1 转存文件
公开
上手 PIP-NN ｜ 训练甲烷深度势能分子动力学模型许晓虎
发布于 2023-07-30
3 赞4 转存文件