何为混沌？从洛伦兹系统理解蝴蝶效应

蝴蝶效应

你听说过“蝴蝶效应”吗？ —— 据说，“一只蝴蝶在巴西轻拍翅膀，可能会导致一个月后德克萨斯州的一场龙卷风。”

在1961年的冬天，美国气象学家Edward Lorenz在使用计算机程序来模拟大气中空气流动的数学模型时发现，在两次计算过程中，只改变了某一中间结果的第三位小数后的精度，便对最终计算结果产生了巨大的影响。他也由此注意到动力学系统对初始条件的敏感性，结合他在气象领域的研究将这种现象不乏诗意地命名为“蝴蝶效应”，并在1993年出版的《混沌学本质》一书中正式将其定义为“动力系统状态的微小变化，将导致后续的状态，与原本可能演变的状态有很大的不同。”

2004年由Eric Bress和J. Mackye Gruber指导的同名科幻电影《蝴蝶效应》也引用了这个概念。Evan来子一个特殊家族，他的父亲与爷爷均因为“精神疾病”而被强制住院。20岁时，他发现自己通过家族遗传获得了可以通过观看承载着过去记忆的信物以改变过去，从而改变现在的能力。他希望改变自己与身边挚友不幸的童年。然而，他真的会成功吗？...

对“蝴蝶效应”这类现象的研究逐渐演化成为了混沌理论(Chaos Theory)———在一个决定性系统中可能产生随机结果。现如今，混沌理论在包括气象学、物理学、航空与航天、生态学、经济学、运筹学、生物学等许多学科与领域中得到了广泛应用。

在本文中，我们将构建一个简单的数学模型——洛伦兹系统，通过对这个系统的求解来尝试理解“蝴蝶效应”背后的混沌行为。

洛伦兹系统的数学求解

方程定义

我们定义一组常微分方程，其中$\sigma$, $\rho$, $\beta$是一组待定参数。

$$\begin{array}{c}\{\begin{array}{rl}\frac{dx}{dt}& =\sigma (y-x),\\ \frac{dy}{dt}& =\rho x-y-xz,\\ \frac{dz}{dt}& =xy-\beta z\end{array}\end{array}$$

使用Runge-Kutta格式进行求解

对于一个初值为$y(a)=y_0$的常微分方程系统

$$\begin{array}{c}\frac{dy}{dx}=f(x,y),a\le x\le b\end{array}$$，

一种常见的常微分方程数值求解方法——Runge-Kuta格式可以被用来进行方程求解，即

$$\begin{array}{c}\{\begin{array}{rl}{y}_{n+1}& =y_n+\frac{h}{8}(K_1+3K_2+3K_3+K_4),\\ K_1& =f(x_n,y_n),\\ K_2& =f(x_n+\frac{1}{3}h,y_n+\frac{1}{3}h{K}_1),\\ K_3& =f(x_n+\frac{2}{3}h,y_n-\frac{1}{3}h{K}_1+h{K}_2),\\ K_4& =f(x_n+h,y_n+h{K}_1-h{K}_2+h{K}_3)\end{array}\end{array}$$

相应的Python代码实现见下。

数值实验1 ：初值条件敏感依存

接下来，我们选择这组参数组合 $\sigma =10,\rho =28,\beta =8/3$，并选择一组差异非常小的初值条件 ${\vec{x}}_0=(0,1,0)$ 和 ${\vec{x}}_1=(0,1,0.002)$ 作为对比实验，来研究初值条件对动力系统演化的影响。

我们从左图的模拟结果中可以看出，即使红线和蓝线的初值条件只在z方向有非常小的扰动(0.002)，但是经过一段时间的演化，两段轨迹已经发生了巨大的偏差。

我们从右图的模拟结果中可以看出，在 $\sigma =10,\rho =28,\beta =8/3$ 这样的一组参数下，体系随时间变化的轨迹具有某种“混沌性”。

数值实验2: 混沌的发生

接下来我们选取 ${\vec{x}}_0=(0,1,0)$ 作为初值，并选取不同的方程参数，让 $\rho$ 从1逐步增加至10,20,100，来研究在不同方程参数的组合下动力系统的混沌性。

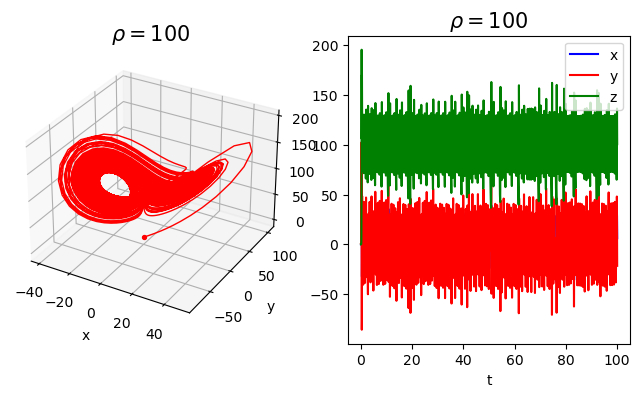
我们可以看出，当 $\rho$ 比较小 $(\rho =1)$ 的时候，动力系统会收敛至其不动点，当时间趋于无穷的时候其极限行为是稳定的。

当 $\rho$ 从 10 增长至 20 的时候，轨迹在空间上的收敛性会消失，但当时间趋于无穷的时候体系振动的幅度会趋于0。

然而，当 $\rho$ 增长至高于20的某一个阈值后，体系轨迹将保持持续震荡，此时，混沌行为就发生了。

最终再让我们看一下，在 $\sigma =10,\rho =28,\beta =8/3$，与初值条件 ${\vec{x}}_0=(0,1,0)$ 和 ${\vec{x}}_1=(0,1,0.002)$时动力系统的轨迹。

看起来像不像一只翩翩起舞的🦋呢？