空间站广场

论文

Notebooks

比赛

课程

Apps

我的主页

我的Notebooks

我的论文库

我的足迹

我的工作空间

任务

节点

文件

数据集

镜像

项目

数据库

公开

伊辛模型——相变问题的万能钥匙

中文

python

Magnetic Material Calculation

中文pythonMagnetic Material Calculation

Cui Yaning

发布于 2023-07-25

推荐镜像 :Third-party software:ai4s-cup-0.1

推荐机型 :c2_m4_cpu

伊辛模型——相变问题的万能钥匙

何为伊辛模型

一维伊辛模型——短暂的失败

二维伊辛模型——希望与重生

三维伊辛模型——未来在哪里？

结语

伊辛模型——相变问题的万能钥匙

代码

文本

作者：Yaning Cui
时间：2023年7月25日

推荐计算资源：CPU
内容：本教程主要介绍伊辛模型的发展与模特卡洛方法实现。
使用方式：您可在 Bohrium Notebook 上直接运行。您可以点击界面上方蓝色按钮 开始连接，选择任何镜像及任何一款节点配置，稍等片刻即可运行。如您遇到任何问题，请联系 bohrium@dp.tech 。
共享协议：本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。

代码

文本

水在冬天结冰，铁在高温中融化，物质形态的突然转变人们很早就接触并利用，但其潜藏的物理秘密直到二十世纪才被揭开。
物质的状态称为“相”，物质状态的转变，如水的凝固，铁的磁性消失等，一种相转变为另一种相的过程称为“相变”。
解开相变问题的万能钥匙，就是伊辛模型（Ising Model）。

代码

文本

伊辛模型的发展历史

1920年：伊辛模型由德国物理学家楞次（Wihelm Lenz）提出以描述铁磁性物质的内部原子自旋状态与宏观磁矩的关系。
1925年：楞次的学生恩斯特·伊辛（Ernst Ising）求解了一维伊辛模型，但没有发现自发磁化的相变现象。
1941年：克拉默斯（Kramers）和瓦尼尔（wannier）研究了二维伊辛模型，并求出了模型的临界温度。
1944年：昂萨格（Lars Onsager）给出了二维伊辛模型在没有外磁场时的解析解，即Onsager解。
1952年：杨振宁给出了二维伊辛模型的完整证明过程。
今天：伊辛模型已经渗透到了物理学以外的学科，可以用来对地震、蛋白质、大脑甚至种族隔离进行建模……

那么，伊辛模型这样一个原本用来研究物质磁性的简化模型，它如何阐明了相变的机制，渗透到各个科学领域呢？

代码

文本

何为伊辛模型

从最初的描述铁磁性质的起源出发，我们假设用布满小箭头的网格表示磁铁，其中每个小箭头表示一个原子，它的指向要么朝上、要么朝下（原子的内禀属性自旋，可以将原子看作一个小磁铁拥有南北两极），每个箭头都会影响与它相邻的箭头，并不断地尝试用磁力翻转它们，使周围箭头的方向和自己保持一致。

楞次注意到，如果大多数原子指向一致，它们各自的微小磁场便会融合，使物体在整体层面表现出磁性，就像磁铁一样。而如果朝上的原子和朝下的原子均匀混合，它们的磁性将会中和，使得整体不会表现出磁性。在高温时，一些磁体会失去磁性，楞次认为，这是因为当温度足够高时，原子的热振动会使原子整体的协同状态崩塌。

代码

文本

一维伊辛模型——短暂的失败

最初伊辛尝试从一维的线性箭矢链出发，其中每个箭头都会受到左右两个相邻箭头的影响。

下文的代码中，我们将两者不同的颜色表示为不同的磁矩方向，通过模特卡洛方法模拟伊辛模型。

代码

文本

[1]

import numpy as np

import random

import matplotlib.pyplot as plt

import matplotlib.animation as animation

def initial_state_1D(size):

# 生成一个随机的初始自旋状态

return np.random.choice([-1, 1], size=size)

def state_show_1D(state):

fig = plt.figure(figsize=(len(state), 1), dpi=40)

ax = fig.add_axes([0, 0, 1, 1])

ax.set_axis_off()

im = plt.pcolor(state.reshape(1, -1), cmap='Wistia', edgecolors="white",linewidths=2, animated=True)

plt.show()

def ising_step_1D(config, temperature):

# 使用Metropolis算法进行一步更新

size = len(config)

for i in range(size):

# 随机选择一个自旋

index = random.randint(0, size-1)

s = config[index]

# 计算自旋的能量变化

nb = config[(index+1) % size] + config[(index-1) % size]

cost = 2 * s * nb

# 根据Metropolis准则判断是否翻转自旋

# cost为候选状态与当前状态的能量差

# temperature是热力学温度

# 意为在低能量差异和高温度下，系统更容易接受新的状态

if cost < 0:

s *= -1

elif random.random() < np.exp(-cost / temperature):

s *= -1

config[index] = s

return config

size = 20 # 自旋链的长度

temperature = 1.5 # 温度

steps = 100 # 模拟步数

config = initial_state_1D(size)

print("初态")

state_show_1D(config)

for i in range(steps):

config = ising_step_1D(config, temperature)

print("末态")

state_show_1D(config)

初态

末态

代码

文本

已隐藏单元格

代码

文本

一维伊辛模拟动态模拟过程

代码

文本

正如上图的模拟所示，伊辛证明，这条一维的箭矢链无法保持磁性。即在任何温度情况下，箭头的随机翻转都会压制磁场，使它们无法保持指向一致。

1925年，伊辛发表了他们的成果，他和楞次认为该结论同样适用于二维和三维的箭矢网格。

History of the Lenz-Ising Model 1920–1950: From Ferromagnetic to Cooperative Phenomena)

他们的模型没有成功解释真实磁铁的特性，这个理论似乎要走入失败。

代码

文本

二维伊辛模型——希望与重生

虽然经历的短暂的失败，但由于数学方法上的突破，伊辛模型在短暂沉寂后又活了过来

1941年，理论物理学家、后来的诺奖得主拉斯·昂萨格（Lars Onsager）尝试研究二维伊辛模型，即每个箭头有四个最近邻而不是两个，并计算在任何给定的温度下，朝上的原子所占的比例。求解这个问题时，需要列出每个箭头对相邻的其他箭头的影响。对于两个距离较远的箭头，两者之间的关系是通过一个一个相邻的箭头传导过去的。在二维平面上，情况远比一维复杂。

昂萨格的解法于1944年发表。计算机学家索林·以色列（Sorin Istrail）称这是一种“非人类”的数学方法，至今仍然很难理解。“你一行一行地跟着他的步骤走，最后发现证明是对的，但你对证明过程却一无所知”。

Crystal Statistics. I. A Two-Dimensional Model with an Order-Disorder Transition

代码

文本

[2]

import numpy as np

import random

import matplotlib.pyplot as plt

import matplotlib.animation as animation

def initial_state_2D(size):

# 生成一个随机的初始自旋状态

return np.random.choice([-1, 1], size=(size, size))

def state_show_2D(state):

fig = plt.figure(figsize=(len(state), len(state)), dpi=10)

ax = fig.add_axes([0, 0, 1, 1])

ax.set_axis_off()

im = plt.pcolor(state, cmap='Wistia', edgecolors="white",linewidths=2, animated=True)

plt.show(block=False)

plt.close()

def ising_step_2D(config, beta):

# 使用Metropolis算法进行一步更新

size = len(config)

for i in range(size):

for j in range(size):

x, y = random.randint(0, size-1), random.randint(0, size-1)

s = config[x, y]

nb = config[(x+1)%size, y] + config[x, (y+1)%size] + config[(x-1)%size, y] + config[x, (y-1)%size]

cost = 2*s*nb

if cost < 0:

s *= -1

elif random.random() < np.exp(-cost*beta):

s *= -1

config[x, y] = s

return config

size = 20 # 网格尺寸

temperature = 1.5 # 温度

steps = 500 # 模拟步数

config = initial_state_2D(size)

print("初态")

state_show_2D(config)

beta = 1.0 / temperature

for i in range(steps):

config = ising_step_2D(config, beta)

print("末态")

state_show_2D(config)

初态

末态

代码

文本

已隐藏单元格

代码

文本

二维伊辛模拟动态模拟过程

代码

文本

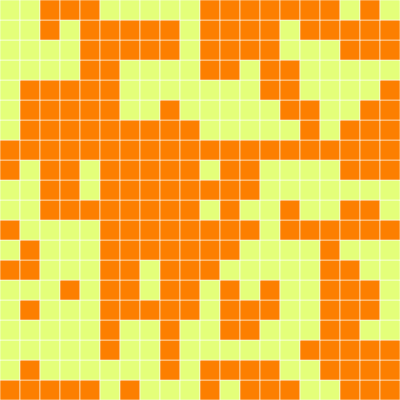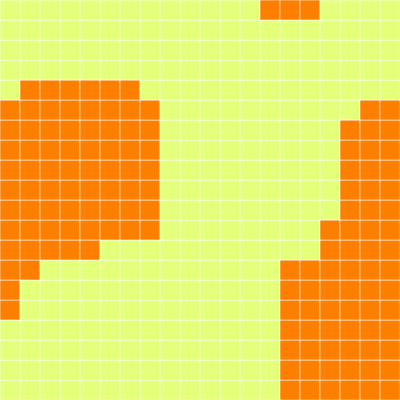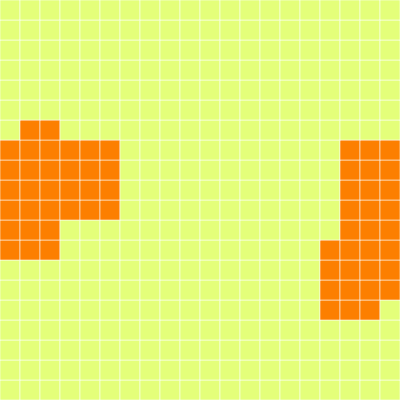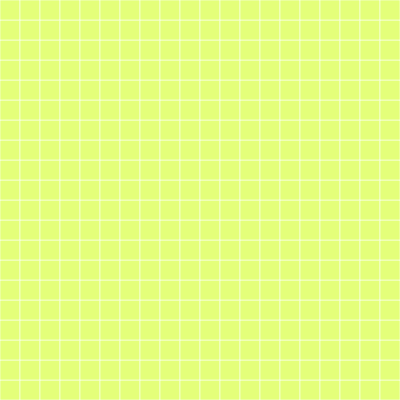
昂萨格最终证明，在二维伊辛模型中，低温时箭头会倾向于保持朝向一致，即磁力将获胜。而当系统超过一个特定的“临界温度”时，无序将会出现，正如同楞次最初猜想的一样。

一个简单的箭矢网格就可以解释相变，而不需要像许多物理学家所想的那样，要考虑真实粒子自带的各种复杂属性。

尽管成功解释了磁性相变，伊辛模型仍然受到质疑。它似乎过于简化，只是展现了一种抽象的现实，因此那时人们对伊辛模型是持怀疑态度的。

代码

文本

随着人们对稀有气体氩和氦的物理特性的精确测定，伊辛模型的处境再次改变。此前昂萨格解出了一系列“临界指数”（critical exponent），来描述在发生相变时，物质的不同属性（例如密度、比热容、磁性等）的变化速度。而实验结果与昂萨格通过理论计算得到的临界指数是吻合的。

尽管大多数物理学家已经接受了楞次和伊辛的模型，但是也同样很好奇：一个物理上不那么真实的模型如何求解出了临界指数这样的具体细节？

代码

文本

答案是，伊辛模型抓住了本质。

History of the Lenz–Ising Model 1950–1965: from irrelevance to relevance

代码

文本

伊辛模型之所以强大，是因为一系列不相关的物质在临近发生相变时，都具有相同的临界指数——现在我们称这种现象为普适性（universality）。

1971年，美国物理学家肯尼斯·威尔逊（Kenneth Wilson）解决了有关普适性的数学问题，并因此获得1982年诺贝尔物理学奖。

Renormalization Group and Critical Phenomena. I. Renormalization Group and the Kadanoff Scaling Picture

代码

文本

三维伊辛模型——未来在哪里？

伊辛模型模型帮助学者们重新理解了很多现象，但目前人们仍然无法求解三维伊辛模型的精确解。

现在计算机能够在合理的精度范围内找到临界指数的近似解，但精确求解三维伊辛模型依然是物理学家近一个世纪的梦想。

代码

文本

结语

伊辛模型自出现之后，就迅速被很多领域的学者用于研究自己的问题。伊辛模型也推动了数值模拟方法的发展，无论是蒙特卡洛还是如今的张量网络方法，都能看到Ising模型的影子。本文也只是描述了伊辛模型的冰山一角，其有更多更加复杂的衍生模型。

感谢您看到这里，不知道伊辛模型对您有何启发呢？

笔者算是半个天文爱好者，初遇伊辛模型时，蹦出了一个脑洞大开的想法：宇宙的起源——奇点的诞生是不是也是一种相变呢？

崔亚宁(cuiyaning@dp.tech)
2023.07.25

代码

文本

中文

python

Magnetic Material Calculation

中文pythonMagnetic Material Calculation

已赞2

本文被以下合集收录

物理

zxh136978

更新于 2024-03-26

1 篇0 人关注

Phase Transition

SchrodingersCat

更新于 2023-12-29

1 篇0 人关注