IC50, EC50, Ki, Kd, Km, k_on, k_off傻傻分不清？蛋白-小分子实验数据详解与清洗（第一期）

前言

预测小分子潜在药物的结合活性，是小分子CADD的核心任务之一。人们为了尽可能快而准确地预测小分子结合活性，发展了从基于分子模拟的 FEP、MMGB/PBSA，Docking 到 AI 预测的一系列方法，并随着 AI for Science 时代的到来，预测精度仍然在不断提升中。

而在同时，我们值得好好审视作为比较或是训练数据的金标准——实验数据。以下问题，希望屏幕前的你，看完 Notebook 后都能给出自信的答案：

• 生化酶活实验得到的抑制常数和基于生物物理手段（如 ITC、SPR 等）得到的抑制常数究竟有何区别，能否等价？与 FEP 计算结果更匹配的是哪一类实验数据？
• 我们常用的参数 IC50 真的能很好的反映出抑制剂的实际抑制强度吗？
• 不同批次的生化酶活实验数据如何换算？
• 将大规模活性数据用于机器学习，有什么合适的弥补实验间差距的方法？

接下来我们就先从这些常见参数的定义说起，然后讨论一下一些容易混淆的参数之间的区别。注：非特别注明，本文涉及到抑制剂时只讨论常见的竞争性抑制剂。

一、实验类型与其活性数据定义

在解释之前先放一张酶学反应式的图，方便后文的说明：

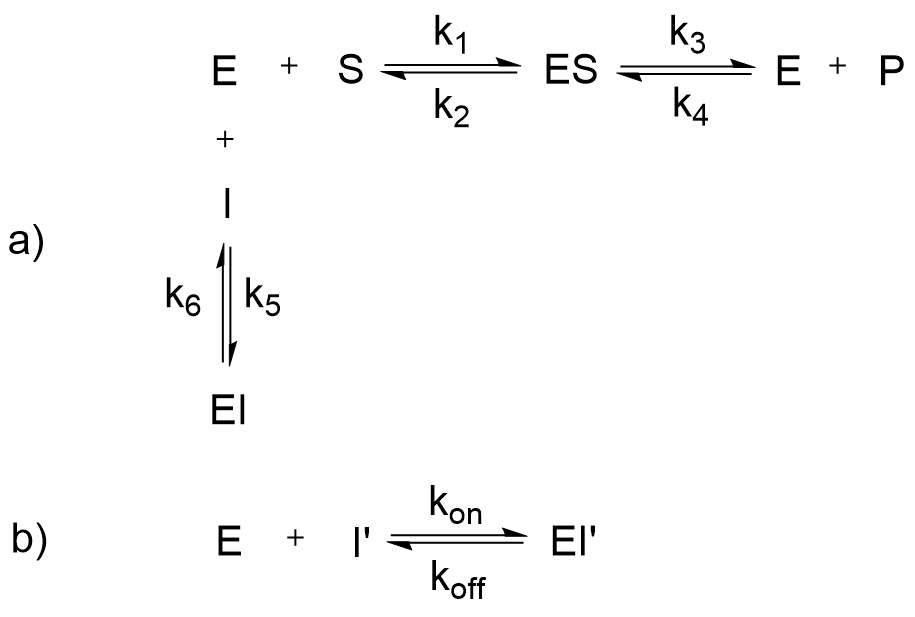
注：E = 酶 enzyme; S = 底物 substrate; ES = 酶-底物复合物中间体; P = 产物 product;

I，I’ = 抑制剂 inhibitor; EI, EI’ = 酶-抑制剂复合物;

$k_x$ = 反应速率常数；[X] = X 的浓度

1.1 生物物理实验（也称 Binding Assay）

生物物理实验测定蛋白（酶）结合抑制剂时，物理信号的变化，如图中 (b) 式。生物物理实验不受到酶促反应的影响，体系中仅存在酶、抑制剂，是更“单纯”的抑制剂结合。

(1) $K_{\mathrm{i}},K_{\mathrm{d}}$, $K_{\mathrm{a}}$

解离常数（dissociation constant），反映的是化合物对靶标的亲和力大小，值越小亲和力越强。

• 化学平衡常数记为 $K_{\mathrm{d}}$ 或 $K_{\mathrm{i}}$，二者等价。

$$K_{\mathrm{i}}\equiv K_{\mathrm{d}}=\frac{{\mathrm{k}}_{\mathrm{off}}}{{\mathrm{k}}_{\mathrm{on}}}=\frac{[\mathrm{E}]\cdot \left[{\mathrm{I}}^{\prime }\right]}{\left[{\mathrm{EI}}^{\prime }\right]}$$

从此公式得出: Kd 为 50% 的酶 E 被抑制剂 I’结合时对应的游离抑制剂的浓度。

• 结合常数（association constant）$K_{\mathrm{a}}=1/K_{\mathrm{d}}$，与 $K_{\mathrm{d}}$ 相反，值越大亲和力越强。
• 结合自由能 $\Delta G_{\mathrm{a}}=-RT\ln K_{\mathrm{a}}=RT\ln K_{\mathrm{d}}$，可与FEP等计算所得的值比较。

(2) ${\mathrm{k}}_{\mathrm{on}}$, ${\mathrm{k}}_{\mathrm{off}}$

• ${\mathrm{k}}_{\mathrm{on}}$ 结合速率常数（association rate constant），代表分子间结合时的快慢，单位为 ${\mathrm{M}}^{-1}\cdot {\mathrm{s}}^{-1}$
• ${\mathrm{k}}_{\mathrm{off}}$ 解离速率常数（dissociation rate constant），代表分子间解离时的快慢，单位为 ${\mathrm{s}}^{-1}$

常见的生物物理实验有等温量热滴定（Isothermal Titration Calorimetry, ITC）、表面等离激元共振（Surface Plasmon Resonance, SPR）等。

1.2 酶生物化学实验（也称 Functional Assay）——酶促反应动力学分析

酶生物化学实验测定的是酶结合抑制剂时，催化能力受到的影响，如图中(a)式。

我们先假设没有抑制剂 I 存在。催化反应进入稳态时，不稳定中间体 ES 浓度稳定，对反应动力学微分方程采用稳态近似法，可得：

$$\begin{array}{c}\frac{\mathrm{d}[\mathrm{ES}]}{\mathrm{d}t}=k_1[\mathrm{S}][\mathrm{E}]-k_{-1}[\mathrm{ES}]-k_2[\mathrm{ES}]\approx 0\\ [\mathrm{ES}]=\frac{k_1[\mathrm{E}][\mathrm{S}]}{k_{-1}+k_2}=\frac{[\mathrm{E}][\mathrm{S}]}{K_{\mathrm{m}}}\\ ⟺[\mathrm{ES}]=[{\mathrm{E}}_{\mathrm{tot}}]\cdot \frac{[\mathrm{ES}]}{[\mathrm{ES}]+[\mathrm{E}]}=[{\mathrm{E}}_{\mathrm{tot}}]\cdot \frac{1}{1+\frac{K_{\mathrm{m}}}{[\mathrm{S}]}}\end{array}$$

(3) $K_{\mathrm{m}}$

• 由此可定义米氏常数 $$K_{\mathrm{m}}=\frac{k_{-1}+k_2}{k_1}$$

• 反应速率

$$r=k_2[\mathrm{ES}]=k_2[{\mathrm{E}}_{\mathrm{tot}}]\frac{1}{1+\frac{K_{\mathrm{m}}}{[\mathrm{S}]}}=V_{\max }\frac{1}{1+\frac{K_{\mathrm{m}}}{[\mathrm{S}]}}$$

米氏常数（Michaelis-Menten constant）, 为酶本身的一种特征参数，其物理意义为当酶促反应达到最大反应速度一半时底物 S 的浓度。$K_{\mathrm{m}}$ 的大小只与酶的性质有关，而与酶的浓度无关，但是随着测定的底物不同、温度、离子强度和 pH 的不同而不同。

1.3 酶生物化学实验——抑制剂存在下的酶促反应动力学分析

那么，当抑制剂 I 存在时，以上方程会有什么影响呢？

以竞争性抑制剂为例，经过同样的推导流程，代入带抑制剂的酶总浓度

$$[\mathrm{ES}]=[{\mathrm{E}}_{\mathrm{tot}}]\cdot \frac{[\mathrm{ES}]}{[\mathrm{ES}]+[\mathrm{E}]+[\mathrm{EI}]}=[{\mathrm{E}}_{\mathrm{tot}}]\frac{[\mathrm{ES}]}{[\mathrm{ES}]+[\mathrm{E}]\left(1+\frac{[\mathrm{I}]}{K_{\mathrm{i}}}\right)}=[{\mathrm{E}}_{\mathrm{tot}}]\frac{1}{1+\frac{K_{\mathrm{m}}}{[\mathrm{S}]}\left(1+\frac{[\mathrm{I}]}{K_{\mathrm{i}}}\right)}$$

可得

$$r=k_2[\mathrm{ES}]=\frac{V_{\max }}{1+\frac{K_{\mathrm{m}}}{[\mathrm{S}]}\left(1+\frac{[\mathrm{I}]}{K_{\mathrm{i}}}\right)}$$

(4) ${\mathrm{IC}}_{50}$, ${\mathrm{EC}}_{50}$ (half maximal inhibitory/effective concentration)

广义的讲，${\mathrm{IC}}_{50}$ 是对指定的生物过程（或该过程中的某个组分比如酶、受体、细胞等）抑制一半时所需的药物或者抑制剂的浓度。药学中用于表征拮抗剂（antagonist）在体外实验（in vitro）中的拮抗能力。${\mathrm{EC}}_{50}$ 是指在特定暴露时间后，能达到 50% 最大生物效应对应的药物、抗体或者毒素等的浓度。药学中除了用于表征体外实验中（in vitro）激动剂（agonist）的激活能力外，还可用于表示达到体内（in vivo）最大生物效应一半时所需的血药浓度。在很多文献中，${\mathrm{EC}}_{50}$ 也用于表征某化合物在细胞水平的效力 (包括激动和拮抗)

——以上定义部分来自参考资料 [1-2]

从定义上能很明显地看出 ${\mathrm{IC}}_{50}$ 和 $K_{\mathrm{i}}$ ($K_{\mathrm{d}}$) 两者的区别，虽然两者都是表征化合物对靶标亲和力的指标，但是 IC50 与实验中所用酶的浓度、底物浓度都有关，而 Ki 是不受这些变量的影响的。目前很多药物化学文献中都不标注自己酶活实验所用酶和底物的浓度，直接给出 IC50 数据，其实这不利于不同文献之间化合物抑制能力的比较，因为 IC50 大小是可以通过酶和底物浓度进行调节的。从这个角度上来说，Ki 才是更加准确的衡量指标，但是为何大多数文献都不用呢？这主要是由于 Ki 的测定过程稍繁琐。IC50 的测定只需要拉出抑制剂浓度梯度进行生长曲线拟合即可方便地得出。然而 Ki 的测定需要先测定该酶特定条件下的 Km，然后在某种抑制剂浓度、不同底物浓度下进行双倒数作图。

根据定义，可通过解方程 $r([\mathrm{I}])=0.5r(0)$ 得到 ${\mathrm{IC}}_{50}$。在不同形式的抑制剂（竞争性、非竞争性）下，${\mathrm{IC}}_{50}$ 与 $K_{\mathrm{i}}$ 的关系如下表（通过副反应系数技巧可以快速推广出所有表达式）：

抑制机理	（初始）反应速率表达式	${\mathrm{IC}}_{50}$ 表达式	$\frac{1}{[\mathrm{S}]}-\frac{1}{r}$ 双倒数图如何计算 $K_{\mathrm{i}}$
竞争性抑制剂：结合游离酶 E	$$\frac{V_{\max }}{1+\frac{K_{\mathrm{m}}}{[\mathrm{S}]}\left(1+\frac{[\mathrm{I}]}{K_{\mathrm{i}}}\right)}$$	$$K_{\mathrm{i}}\frac{K_{\mathrm{m}}+[\mathrm{S}]}{K_{\mathrm{m}}}$$	$$\frac{斜率}{截距}=K_{\mathrm{m}}\left(1+\frac{[\mathrm{I}]}{K_{\mathrm{i}}}\right)$$
反竞争性抑制剂：结合酶-底物复合物 ES	$$\frac{V_{\max }}{\left(1+\frac{[\mathrm{I}]}{K_{\mathrm{i}}}\right)+\frac{K_{\mathrm{m}}}{[\mathrm{S}]}}$$	$$K_{\mathrm{i}}\frac{K_{\mathrm{m}}+[\mathrm{S}]}{[\mathrm{S}]}$$	$$\frac{斜率}{截距}=\frac{K_{\mathrm{m}}}{1+\frac{[\mathrm{I}]}{K_{\mathrm{i}}}}$$
非竞争性抑制剂：同强度结合 E 和 ES	$$\frac{V_{\max }}{\left(1+\frac{[\mathrm{I}]}{K_{\mathrm{i}}}\right)+\frac{K_{\mathrm{m}}}{[\mathrm{S}]}\left(1+\frac{[\mathrm{I}]}{K_{\mathrm{i}}}\right)}$$	$$K_{\mathrm{i}}$$	$$截距=\frac{1+\frac{[\mathrm{I}]}{K_{\mathrm{i}}}}{V_{\max }}$$（需测定无抑制剂下 $V_{\max }$）
混合竞争性抑制剂：不同强度结合 E 和 ES	$$\frac{V_{\max }}{\left(1+\frac{[\mathrm{I}]}{\alpha K_{\mathrm{i}}}\right)+\frac{K_{\mathrm{m}}}{[\mathrm{S}]}\left(1+\frac{[\mathrm{I}]}{K_{\mathrm{i}}}\right)}$$	$$K_{\mathrm{i}}\frac{K_{\mathrm{m}}+[\mathrm{S}]}{K_{\mathrm{m}}+\alpha [\mathrm{S}]}$$	$$\frac{斜率}{截距}=K_{\mathrm{m}}\frac{1+\frac{[\mathrm{I}]}{K_{\mathrm{i}}}}{1+\frac{[\mathrm{I}]}{\alpha K_{\mathrm{i}}}}$$（需测定无抑制剂下 $V_{\max }$，根据截距求$\alpha$）

参考资料:

[1] wikipedia: https://www.wikipedia.org/

[2] 王镜岩等，《生物化学》上册，高等教育出版社，第九章

[3] Cheng Y, Prusoff WH Biochem Pharmacol. 22 (23): 3099–108

二、不同实验测得活性对比

文献 [3] 中收录了通过 BindingDB 获取的有2种以上实验数据对比的化合物系列。我们来作个图。

可见，生物物理实验两两之间、生物化学实验两两之间，吻合度大于 生物物理实验vs生物化学实验。

我们可以认为，$\Delta G$ 的实验随机误差在 0.75 kcal/mol 以内，$\Delta \Delta G$ 的实验随机误差在 0.91 kcal/mol 以内。

三、数据使用建议与清洗实践

BindingDB 是目前最大的结合活性数据集。其中的 Validation Set 汇总了通过分子相似性归类的化合物系列，非常适合用于比较相对活性差距。

然而，Validation Set 中包含了许多由多篇文献拼合成的 Chemical Series，由于文献实验类型和条件不同，实际上文献间不可比。

因此，若想仍然保留多篇文献拼合成的 Chemical Series 而不将其切分为单篇文献，就需要根据 3.3 中的表格换算。酶的米氏常数可以通过查找 BRENDA-enzymes 数据库 获得。

对大量文献中的 Binding Affinity 实验 protocol 提取，可以使用大语言模型。

从另一个角度，既然实验间的校准这么困难，我们可以仅使用实验内的相对值作为比较和训练目标。这是我们下一期的主题！