关于经典分子动力学模拟，不可不知的力场知识

作为一个资深的分子动力学模拟从入门到入土患者 🥹 ，第一次看到Bohrium Notebook的推送，简直瞪大不大的双眼，心想难道破土🌼而出的机会来了？！又因为笔者学过的理论和公式，考完试就还给老师了😂 。所以，本文只涉及牛顿力学和基础的微积分知识，对入门者友好。费曼学习法告诉我们，输出是最好的输入。写一个Notebook倒逼自己输出一下。如果能帮到入门者一点点，那就太好啦~

分子动力学为什么能作为强大的工具揭开微观世界的奥秘呢？咱们还得从物理学的祖师爷牛顿聊起。

艾萨克·牛顿（Isaac Newton）爵士（尊称牛爵爷），于1687年发表了《自然哲学的数学原理》。这本书多重要呢？牛顿三大运动定律首次在这本书中发表，不仅如此，牛爵爷还在书中天才地论证了地面物体与天体的运动都遵循着相同的自然定律。牛爵爷的传奇故事有很多，咱们重新聊回牛顿运动定律。

牛顿运动定律，一言以蔽之，曰：给我初始条件，我就能预测未来。

假设一个质量为$m$的粒子，沿$x$轴运动并受某些力$\vec{F}(x,t)$的影响。经典力学的任务是确定粒子在任意给定时间的位置：$\vec{x}(t)$。一旦我们知道了位置信息，就可以由下面的运动学公式计算出速度、动量、动能，或其他感兴趣的动力学变量

$$\vec{v}=\frac{d\vec{x}}{dt},\vec{p}=m\vec{v},T=\frac{1}{2}m{\vec{v}}^2.$$

那么如何预测$\vec{x}(t)$呢？我们需要应用牛顿第二运动定律， $$\vec{F}=\frac{d\vec{p}}{dt}=m\vec{a}.$$

对于保守系统，力可以表示为势能函数的导数。就是这么巧，微观体系（例如原子、分子和粒子）通常被视为保守系统。这是因为在微观尺度下，四种基本相互作用（引力、电磁相互作用力、弱相互作用力、强相互作用力），通常只需要考虑电磁相互作用，而电磁力是保守力。那么现在，力的表达式又可以写为， $$\vec{F}=-\frac{\partial V}{\partial x}{\vec{e}}_x.$$

此时，牛顿第二定律的方程可以写为， $$\frac{d^{2}x}{d{t}^2}=-\frac{\partial V}{\partial x}.$$

现在，给出具体的初始条件和势能函数形式，就可以预测单个质点未来的运动轨迹了。举个弹簧振子例子。代码实现如下：

单个质点的运动学和动力学方程可以通过叠加原理推广到质点系。此处省略推广。

现在考虑真正的微观世界。联系宏观世界和微观世界的常量是阿伏伽德罗常量（Avogadro constant），它的数值为6.02214076×10²³。后牛顿时代的科学家在牛顿力学的基础上，用概率统计的方法，建立了对由大量粒子组成的宏观物体的物理性质及宏观规律作出微观解释的理论物理学分支，统计力学。分子动力学的本质是统计力学的计算机实现，也被称为“拉普拉斯牛顿力学的展望”，即通过模拟自然力并洞察原子尺度上的分子运动来预测未来。

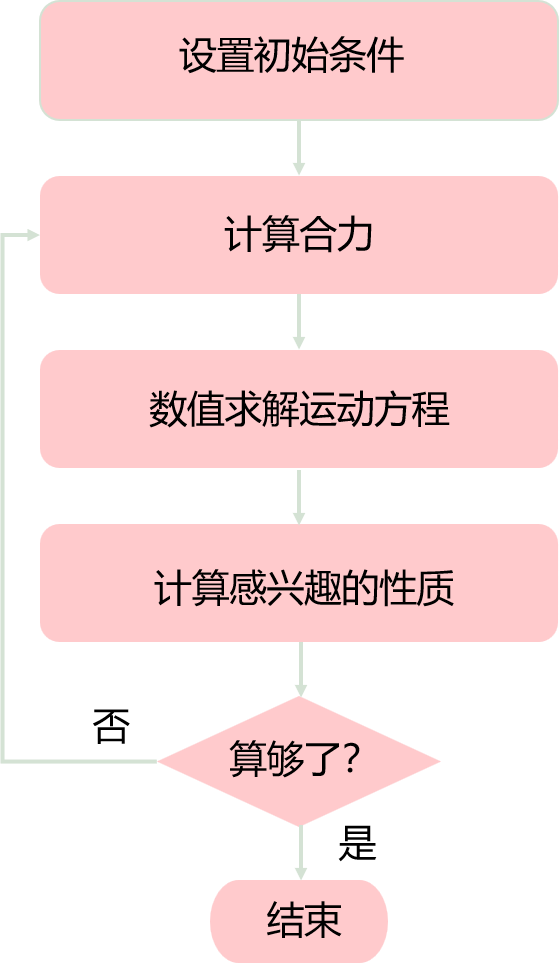
分子动力学来源于一个朴素的想法：从原子尺度对真实世界建模，如果知道原子和分子之间的相互作用的描述，那么设定初始条件后，就可以运用牛顿第二定律更新研究对象的运动轨迹，然后根据统计力学计算出感兴趣的性质，从而解释研究对象。

分子动力学模拟涉及的模型和算法如下所示。本文展开讨论势函数/力场模型。

Garbage in, garbage out

合理性意味着有效性，但有效性并不意味着合理性

上面的原则同样适用与选取分子动力学模拟的势函数或力场。力场模型的质量直接决定了模拟结果的好坏。

首先说明，物理学家习惯将描述多粒子体系中粒子之间相互作用的势能函数称为势函数，化学家称为力场，都是一回事儿。

根据叠加原理，多粒子体系总的势能可以写成单个粒子的势能加和， $$U=\sum _i{U}_i.$$

如何表示单个粒子的势能$U_i$？若只考虑两体相互作用，就是对势，势能函数可以写成以下形式： $$U=\frac{1}{2}\sum _i\sum _{j\ne i}{U}_{ij}\left(r_{ij}\right),$$

若考虑三体及以上的相互作用，就是多体势，比如笔者使用过的Tersoff势函数。Tersoff势函数的表达式为： $$U_i=\frac{1}{2}\sum _{j\ne i}{f}_C(r_{ij})\left[f_R(r_{ij})-b_{ij}{f}_A(r_{ij})\right].$$

其中， $f_C$ 是一个截断函数，当 $r_{ij}<R$ 时取值为 1，当 $r_{ij}>S$ 时取值为 0。截断函数为，

$$f_C(r_{ij})=\frac{1}{2}\left[1+\cos \left(\pi \frac{r_{ij}-R_{ij}}{S_{ij}-R_{ij}}\right)\right].$$

排斥函数 $f_R$ 和吸引函数 $f_A$ 为

$$f_R(r)=A{e}^{-\lambda r_{ij}};$$

$$f_A(r)=B{e}^{-\mu r_{ij}}.$$

键序为

$$b_{ij}={\left(1+{\beta }^n{\zeta }_{ij}^n\right)}^{-\frac{1}{2n}},$$

其中，

$${\zeta }_{ij}=\sum _{k\ne i,j}{f}_C(r_{ik})g_{ijk},$$

$$g_{ijk}=1+\frac{c^2}{d^2}-\frac{c^2}{d^2+(h-\cos {\theta }_{ijk}{)}^2}.$$

在以上表达式中，有如下参数： $A$, $B$, $\lambda$, $\mu$, $\beta$, $n$, $c$, $d$, $h$, $R$, $S$。

力场通常用来描述分子体系。分子力学中的势能包括键合项，用于描述由共价键连接的原子间的相互作用，以及非键合项（也称为非共价项），用于描述长程静电和范德华力。 $$E_{total}=E_{bonded}+E_{nonbonded}$$

其中，共价和非共价贡献的组成部分由以下求和式给出。 $$E_{bonded}=E_{bond}+E_{angle}+E_{dihedral}$$

$$E_{nonbonded}=E_{electrostatic}+E_{VandeWaals}$$

不同的力场模型对于分子力场的每一项的表达式略有不同。下面举一个描述键相互作用的典型模型。

这个化学键模型假设化学键的振动满足胡克定律，弹簧振子模型又出现了。它的图像如下图所示。

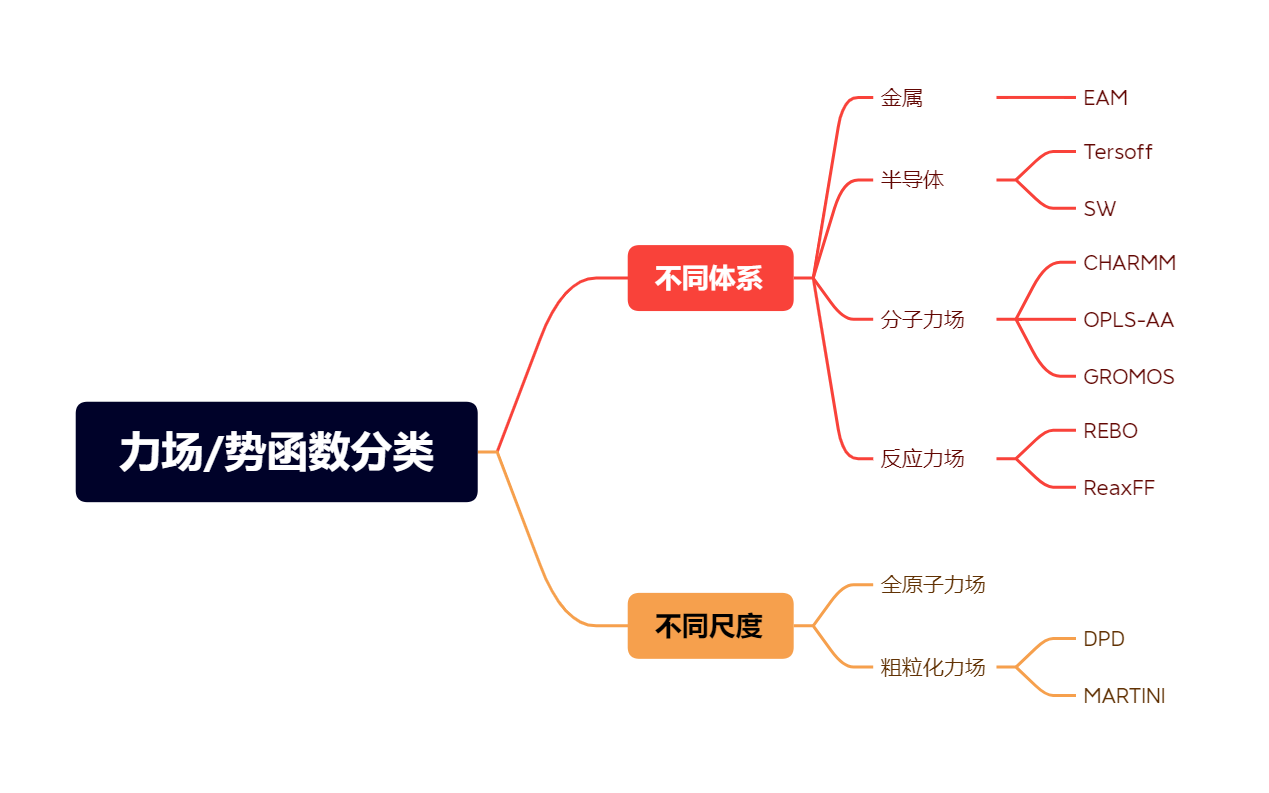
根据不同的分类标准，可以有不同的力场分类。力场的分类如下图所示，图中没有完全枚举所有的力场模型，读者可以继续补充。

力场的选择通常需要以下问题：

• 所研究体系包含哪些相互作用
• 研究的体系的空间尺度
• 研究的问题的时间尺度
• 是否考虑极化、量子效应
• 是否发生化学反应

通常，多体势模型比对势模型准确，反应力场比分子力场准确，但是同时，也更消耗资金和时间，需要综合考虑准确和效率问题。

关于分子体系力场如何选择可以参考李继存老师的博文博文链接。

这是一个经典势函数库链接Interatomic Potentials。

对于做应用的科研人员来说，通常找力场的流程是：

1. 在文献中寻找相似的体系使用的力场；
2. 验证该力场是否适用于自己的课题；
3. 如果适合，开始课题研究；
4. 如果不适合，改进找到的力场（比较难）；
5. 没有找到力场，开发新力场（巨难且耗时）。

经验力场本来的劣势，

• 可转移性差 当势项的函数形式变化时，来自一个原子间势函数的参数通常不能与另一原子间势函数一起使用。
• 精度不够 大多数力场依靠点电荷来重现分子周围的静电势，这种模型对各向异性电荷分布效果描述较差

DeePMD-kit（Deep Potential Molecular Dynamics kit）是一个用于分子动力学模拟的开源软件包，它基于深度学习技术，用于构建和训练深度势能模型（Deep Potential）。

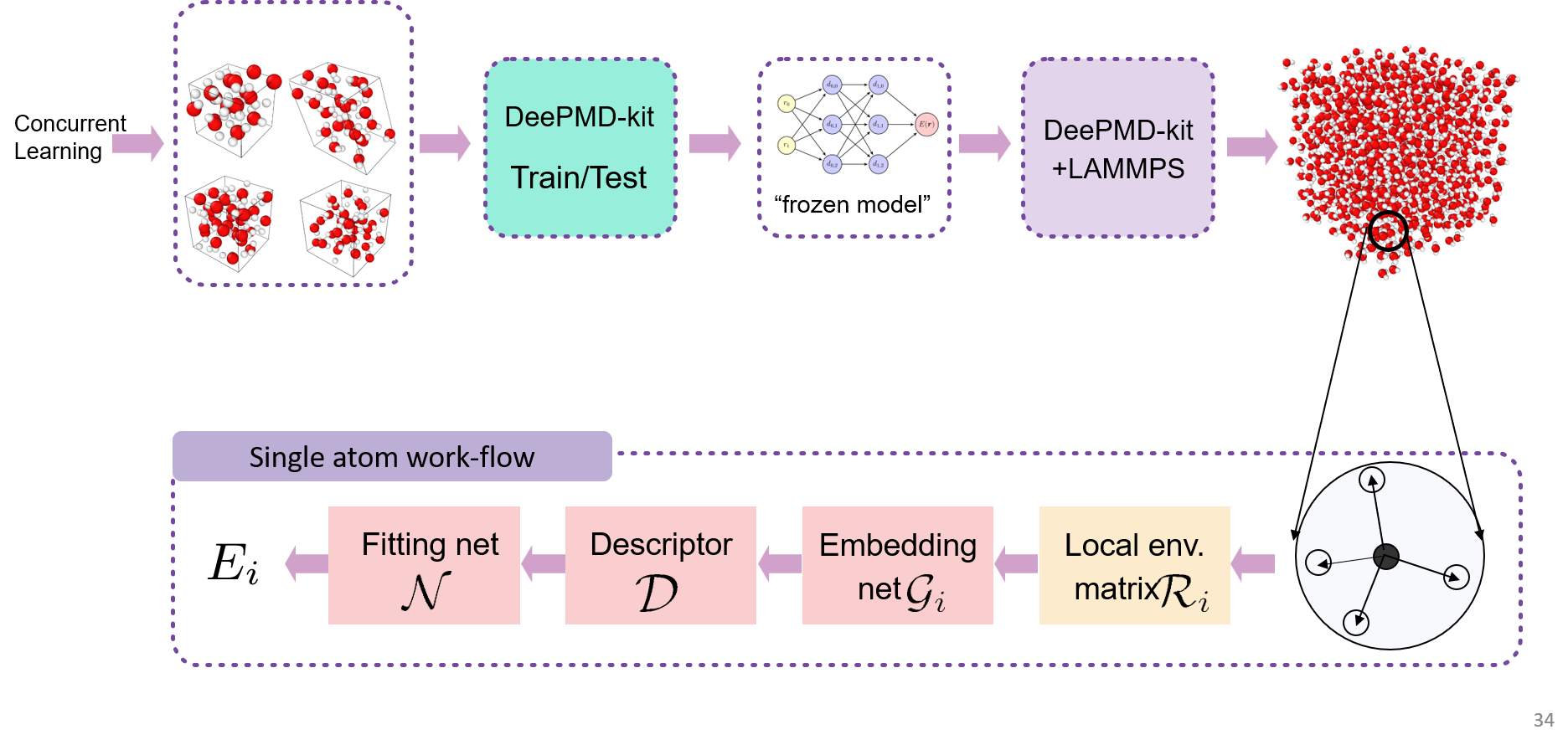
DeePMD-kit 的主要目标是通过使用深度神经网络来学习原子系统的势能面，并在分子动力学模拟中应用这些学习到的势能模型，以加速分子模拟的速度。相对于传统的计算量子化学方法，使用深度势能模型可以显著减少模拟的计算成本，从而允许更大规模、更复杂的分子系统进行模拟研究。

深度势能模型本质上是多体势模型，使用DeePMD-kit训练深度势能模型的流程如下图所示。

训练深度势能模型的开源工具包DeePMD-kit的出现，使以前很多没有合适的工具进行模拟的研究问题变为了可能。

探索案例见DeepModeling社区的文献。未来探索者可以在此页面初步分析研究的问题是否可以使用深度势能模型解决。

笔者看来，AI for 分子动力学模拟未来的趋势：

• 覆盖元素周期表的大模型
• 更好的机器学习模型