Diffusion Models初探：你还是不懂扩散模型的基本原理？

摘要：本文介绍并实现了一维扩散模型的前向和反向过程，验证了一维扩散模型前反向过程的一致性；并进一步提出了两个朴素模型，最近邻与最大似然模型，以验证一维扩散模型正确性。

一、简介

深度扩散模型(Diffusion Models)是一类基于深度学习的生成模型，近年来在图像和文本生成方面取得了很大的进展。

它的基本思想是从完整的信号开始，逐步向添加噪声的方向进行，每一步只对信号做很小的改变。然后，利用深度神经网络从添加了噪声的信号中恢复原始完整的信号。 具体来说，深度扩散模型包含一个Forward过程和一个Backward过程：

• Forward过程：逐步将原始数据加入噪声，得到添加了不同程度噪声的数据序列。

• Backward过程：使用神经网络从加噪的数据中逐步恢复更清晰的数据，最终输出质量高的新样本。

同时，宋飏等人的工作将此类扩散模型与伊藤扩散（Ito Diffusion）的前向与反向随机微分方程联系在一起，他们证明DDPM是伊藤过程的一种随机离散（当然这也是模型最初取名叫Diffusion Models的题中之义），并提出另外的几种随机过程的构建形式。

本Bohrium Notebook将初探Diffusion Model的前向与反向过程，验证两个过程之间的等价性。

二、伊藤扩散与DDPM（前向过程）

根据定义，伊藤扩散由以下的SDE定义：

$dx=f(x,t)dt+g(x,t)dw$

其中$f(x,t)$为漂移项，$g(x,t)$为扩散项。 而当我们取$f(x,t)=-\frac{1}{2}\beta (t)x,g(x,t)=\sqrt{\beta (t)}$时，上述的随机微分方程转为

$dx=-\frac{1}{2}\beta (t)xdt+\sqrt{{\beta }_t}dw$

这便定义了扩散模型的前向过程：如果我们在$x(0)=x_0$的边界条件下解此随机微分方程，将得到每个时刻的概率分布

$p(x,t)=\mathcal{N}\left(x;\sqrt{\gamma (t)}{x}_0,(1-\gamma (t))I\right)$ ，其中$\gamma (t)=exp\left(-{\int }_0^t\beta (s)ds\right)$

（得到$p(x,t)$的具体过程可以参考Simo Särkkä and Arno Solin: Applied Stochastic Differential Equations, Section 5.5）

这意味着，每个时刻下$x$的分布都是以缩放后的$x_0$为均值的某个高斯分布。因此，我们可以将其写为确定性的均值与随机性的方差两部分：

$x(t)=\sqrt{\gamma (t)}x(0)+\sqrt{1-\gamma (t)}ϵ(t)$

其中$ϵ(t)$为标准高斯分布的随机变量。 而当我们对照DDPM的前向过程

$x_t=\sqrt{\overline{{\alpha }_t}}{x}_0+\sqrt{1-\overline{{\alpha }_t}}{ϵ}_t$

就会发现，选取合适的$\bar{\alpha }$与$\gamma$后，两者是完全一致的！ 这为我们分析DDPM模型的dynamics提供了很重要的帮助。

当然，上述的$x(t)$还可以写为任意一个给定的$x(s),s<t$的函数：

$x(t)=\sqrt{\frac{\gamma (t)}{\gamma (s)}}x(s)+\sqrt{1-\frac{\gamma (t)}{\gamma (s)}}ϵ(t)$

如果我们令$\zeta (t,s)=1-\frac{\gamma (t)}{\gamma (s)}$，那么我们将得到

$x(t)=\sqrt{1-\zeta (t,s)}x(s)+\sqrt{\zeta (t,s)}ϵ$

不难验证这与DDPM的step-wise forward过程

$x_t=\sqrt{1-{\beta }_t}{x}_{t-1}+\sqrt{{\beta }_t}{ϵ}_t$

是一致的。

三、实现一个前向过程

前向过程的形式还是十分简单的。我们构建一个$\gamma$函数，并将其作为参数进行$x,ϵ$的线性组合即可。

这里我们使用一个$e^{-k{t}^4}$形式的$\gamma$，这样相当于在diffusion model中使用立方的${\beta }_t$。

接下来我们构造一个代表数据分布的、初始的$x_0$分布，例如80%的+1和20%的-1。我们打印出数据分布的均值，约为0.6：

下面，我们构造一个step-wise的前向过程，将t在[0,1]区间内离散100份。

最后，我们将得到的trajectory画出来：

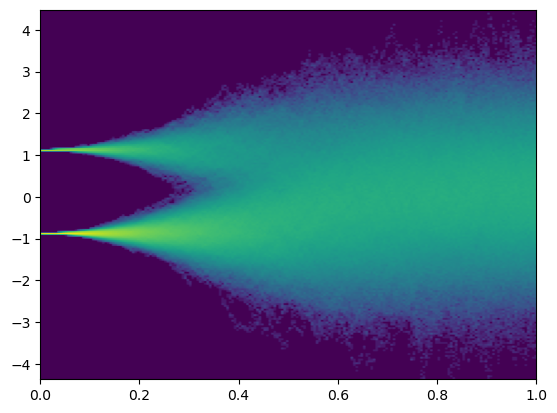
可以看到，正向的SDE可以正确的将在{-1, 1}支撑的两点分布平滑的过渡到N(0,1)的高斯分布。

四、反向SDE与实现

借由Fokker-Planck-Kolmogorov公式，我们可以推知反向过程应该服从的SDE：

$dx=\left[f(x,t)dt-g(x,t{)}^2{\nabla }_{x_t}\log p(x,t)\right]d\bar{t}+g(x,t)d\bar{w}$

此处$d\bar{w}$为反向的Wiener过程。

代入系数进行化简后，我们可以得到反向过程的形式：

$x(s)=\frac{1}{\sqrt{1-\zeta (t),s}}\left(x(t)+\zeta (t,s)\cdot s(x(t),t)\right)+\sqrt{\zeta (t,s)}ϵ(t)$

因为我们显式得到了$p(x,t)$，因此对应的score function $s(x(t),t)={\nabla }_x\log p(x(t),t)$也可以显示计算：

${\nabla }_{x_t}\log p(x,t)=\frac{\sqrt{\gamma (t)}x(0)-x(t)}{1-\gamma (t)}$

因此我们可以实现以下的反向过程并打印出最终的均值：

可以看到，预测的$x_0$和真实的$x_0$的均值是相同的。

最终，我们画出反向SDE的图像，可以看到和正向的SDE图像相一致。

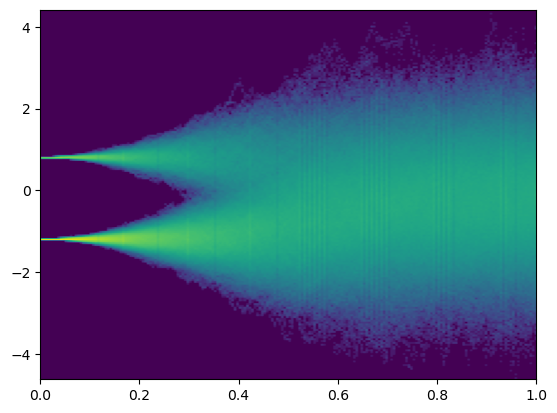
五、为反向过程引入噪音

最后，如果我们用不相关的噪声，污染每步用于计算score function的$x_0$以模拟模型训练的不足呢？我们定义以下的反向过程：

然后测试noise=0.1和1.0的两种情况：

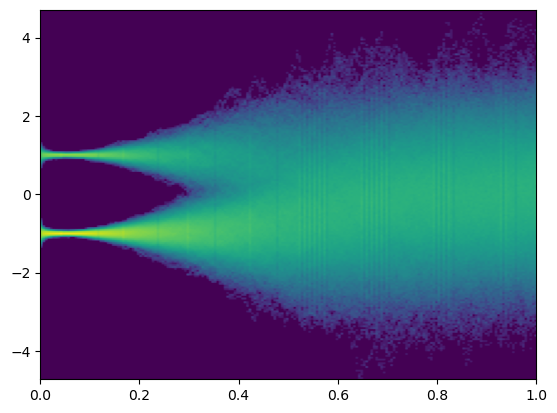
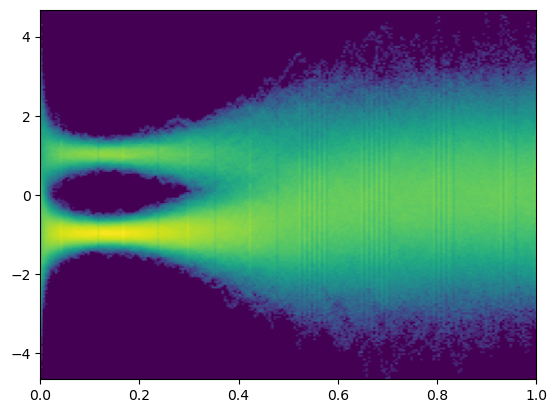
可以看到，在噪音较小时，反向的SDE仍可以有效地复原$x_0$；但随着噪音增大，这样的复原便不再可行。

六、利用Nearest Neighbor构建最简单的模型

在四、五中，我们都是利用已知的标签来计算score function；而当他们未知时，我们就需要用模型学习反向过程，这将极大地增大完全复现反向SDE的难度。

下面我们将利用Nearest Neighbor的思路构建一个最简单的模型，即当$x_t>0$时，我们认为$x_0=1$，反之为$-1$。

让我们看看结果：

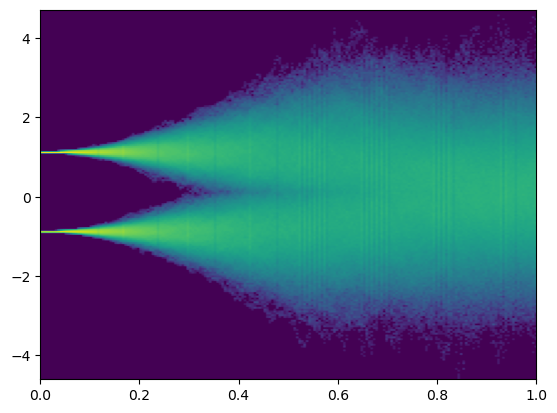
可以看到，反向的SDE的图像似乎和正向的还是很像的；但是最终预测的$x$的分布和真实不同：均值从约0.6降至了0。这是因为此分类器并未考虑$x_0$本身的先验分布，而是贪心的将样本分给最近的峰值。

七、构建一个MLE模型

进一步的，我们发现，既然我们已知$p(x_t|x_0)$与$p(x_0)$，那么我们可以通过贝叶斯公式构建一个更好的MLE模型：

$p_t(x_0|x_t)\propto p_t(x_t|x_0)p(x_0)=\mathcal{N}(x_t;\sqrt{\gamma (t)}{x}_0,1-{\gamma }_t)\cdot p(x_0)$

比较$p_t(x_0=+1|x_t)$与$p_t(x_0=-1|x_t)$：

$p_t(x_0=+1|x_t)\propto \exp \left\{-\frac{(x_t-\sqrt{{\gamma }_t}{)}^2}{2(1-{\gamma }_t)}\right\}\eta$

$p_t(x_0=-1|x_t)\propto \exp \left\{-\frac{(x_t+\sqrt{{\gamma }_t}{)}^2}{2(1-{\gamma }_t)}\right\}(1-\eta )$

此处$\eta =0.8$为生成$x_0$时选取的$x=+1$的比例。

注意到$p_t(x_0=+1|x_t)>p_t(x_0=-1|x_t)$当且仅当

$\exp \left\{-\frac{(x_t-\sqrt{{\gamma }_t}{)}^2-(x_t+\sqrt{{\gamma }_t}{)}^2}{2(1-{\gamma }_t)}\right\}>\frac{1-\eta }{\eta }$

即

$x_t>\frac{1-{\gamma }_t}{2\sqrt{{\gamma }_t}}\ln \frac{1-\eta }{\eta }$

我们由此得到了一个MLE分类器。

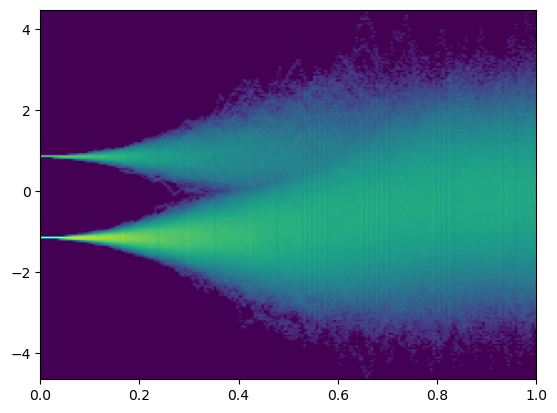
可以看到，通过考虑$x_0$部分的prior分布，均值部分得到了修正。