空间站广场

论文

Notebooks

比赛

课程

Apps

我的主页

我的Notebooks

我的论文库

我的足迹

我的工作空间

任务

节点

文件

数据集

镜像

项目

数据库

公开

AI for Science——漫步结构搜索

中文

AI4S

python

Tutorial

步道

中文AI4SpythonTutorial步道

小锡兵

发布于 2023-08-04

推荐镜像 :DeePMD-kit:devel-b0b2b73d

推荐机型 :c2_m4_cpu

AI for Science——漫步结构搜索

一、AI for Science背景介绍

1.什么是AI for Sience？

2.AI for Science 助力科学的第四范式

二、结构搜索背景介绍

1.晶体与晶体结构

2.图论

3.势能面

三、晶体结构搜索算法

下面是一个通过粒子群优化（PSO）算法寻找势能面极小值的一个python代码演示

四、机器学习力场

五、结构搜索软件介绍

1.软件介绍

2.快速上手

六、结构搜索应用

七、总结＆展望

AI for Science——漫步结构搜索

代码

文本

作者: 黄冠 695139851@qq.com

创建日期: 2023-08-1

描述: 本教程不可以在 Bohrium Notebook 上直接运行，请在Bohrium节点控制台中，创建新节点-创建容器节点，镜像选择任何一款节点配置运行。

如您遇到任何问题，请联系 695139851@qq.com 。

共享协议: 本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。

代码

文本

一、AI for Science背景介绍

代码

文本

1.什么是AI for Sience？

AI for Science(人工智能助力科学)是指利用人工智能技术来帮助和加速科学研究与科技创新的一个快速发展的新兴领域。AI for Science的主要目的是通过机器学习、深度学习等人工智能算法来分析海量、高维复杂的科研数据,帮助科学家发现规律和趋势,建立模型,辅助进行科学假说的构建和验证。

图片来源：Scientific discovery in the age of artificial intelligence

代码

文本

2.AI for Science 助力科学的第四范式

2007年，图灵奖得主吉姆.格雷提出了数据密集型科研“第四范式”。他将大数据科研从第三范式，即计算机模拟中分离出来，独立作为一种科研范式，单独分离出来的原因是大数据的研究方式，不同于基于数学模型的传统的研究方式。

第一范式：实验科学

以记录和描述自然现象为主的实验科学，比如钻木取火，到1590年，伽利略在比萨斜塔上做了“两个铁球的同时落地”的实验，得出了重量不同的两个铁球同时下落的结论，推翻了亚里士多德的结论：“物体下落的速度与重量成比例”的学说，纠正了这个持续了1900年之久的错误结论；

第二范式：理论科学

利用模型归纳总结过去记录的现象，人类采用数学，几何，物理等理论，构建问题模型和解决方案，例如牛顿三定律和麦克斯韦方程等为代表的理论科学，这些理论的广泛传播和运用对人们的生活和思想产生了极大的影响，在很大程度上推动了人类社会的发展；

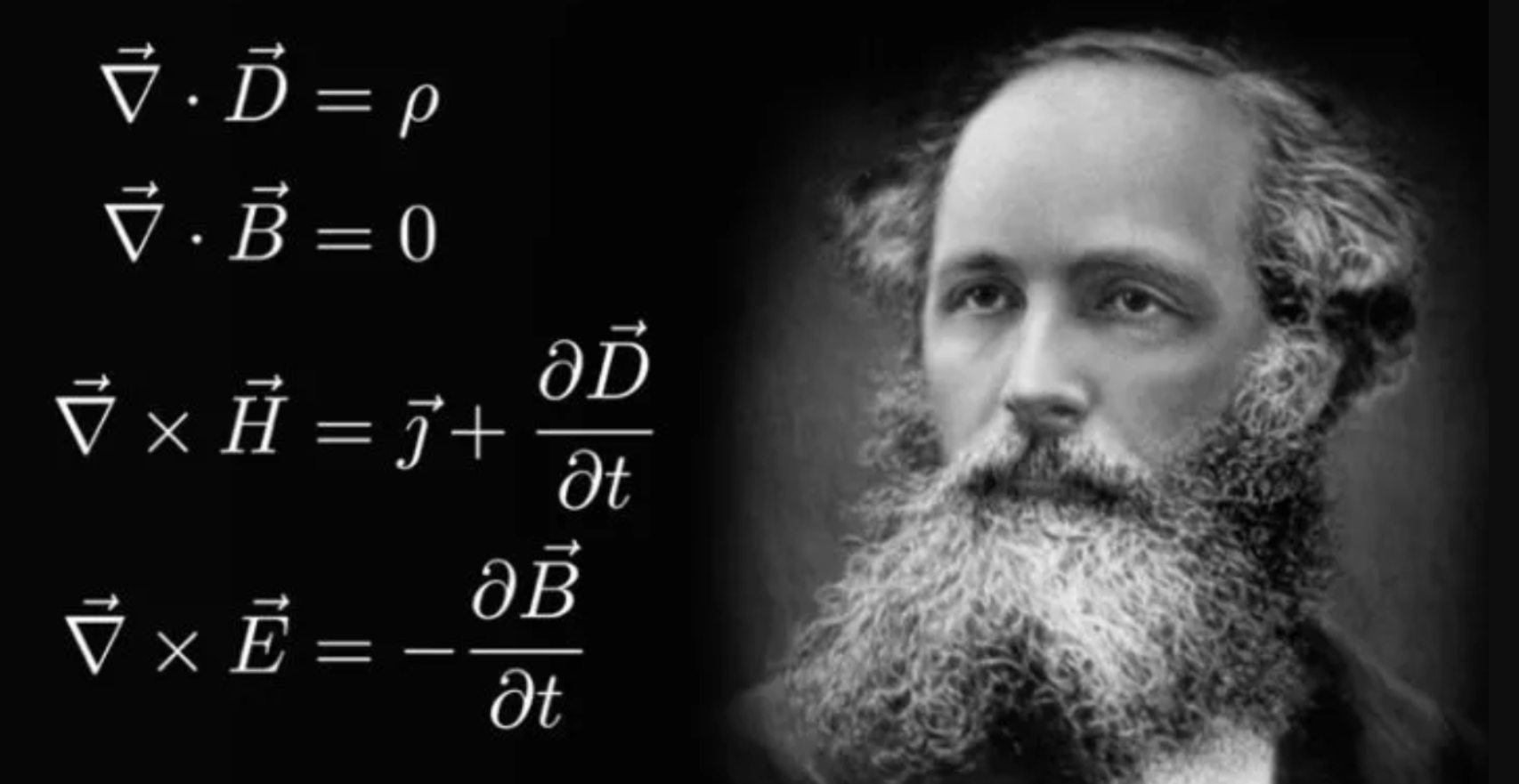
第三范式：计算科学

随着计算机的运算能力越来越强大，它逐渐被用于科学研究领域。同前两个范式不同，计算科学中诞生了一种崭新的技术工具：计算模型与系统模拟。这一工具利用计算机的计算能力、基于大规模并行的计算机体系结构、通过设计算法并编制程序来模拟复杂过程，在大气环流、核反应过程、病毒感染过程。在经济学、心理学、认知科学等缺乏简单、直观分析解决方案的领域获得广泛采用。

第四范式：数据科学

在大数据时代采用数据驱动的方式进行研究，通过收集大量的数据，让计算机去总结规律的数据密集型科学。AI for Science结合了AI和第四范式的优点，旨在利用AI技术加速科学研究。

AI for Science的兴起有两个主要的驱动因素：一数据的爆炸式增长，二是计算能力的飞速提升。在生物学、天文学、社会科学等领域，数据的收集和存储已经超出了人类的分析和理解能力。而AI，特别是深度学习（deep learning），可以通过构建人工神经网络（artificial neural network），自动地从大量的数据中提取特征和模式，从而实现对数据的高效处理和挖掘。另一方面，随着云计算、量子计算、神经元计算等技术的发展，计算能力也得到了前所未有的提升，使得AI可以处理更复杂、更高维度、更多变量的问题。

参考链接：AI for Science：人工智能助力科学探索的新范式

代码

文本

二、结构搜索背景介绍

代码

文本

1.晶体与晶体结构

代码

文本

晶体结构是指固体中由原子、离子或分子等构成的一种有序的空间排列方式。我们生活中的材料绝大多数属于固体，其中大多数材料中质点的排列具有周期性和规则性，属于晶态材料。不同的晶体，其质点间结合力的本质不同，质点在三维空间的排列方式不同，使得晶体的微观结构各异，反应在宏观上，不同的晶体有截然不同的性质。例如我们生活中最熟悉食盐，它的主要成分NaCl，是由Na离子与Cl离子相互形成离子键，以六方最密堆积的方式周期性排列。我们只有了解了微观粒子的晶体结构，才能更好的进行材料的性质研究。因此，晶体结构是材料研究的起点和基础。

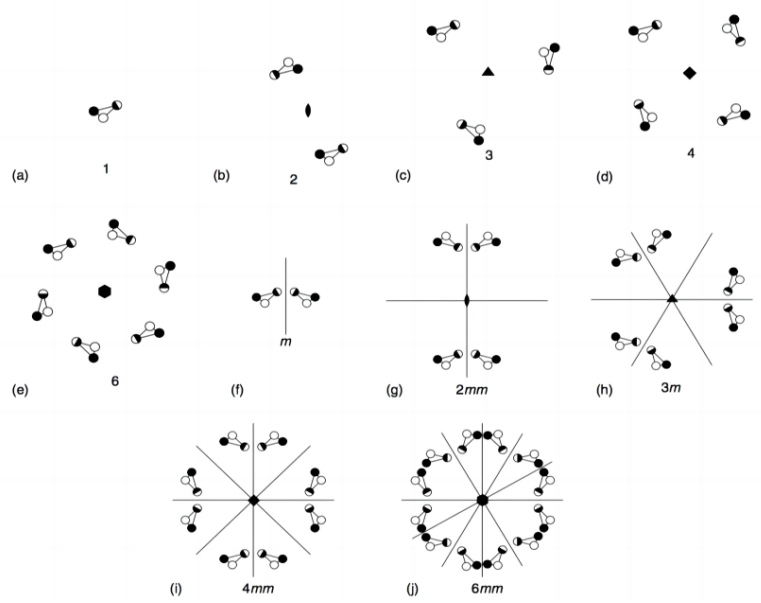
点群(point group):当晶体中全部宏观对称元素至少交于一点，将这些对称元素全部收敛于一点的各种组合称为晶体的点群。以二维平面为例，一共有10种点群如下图所示：

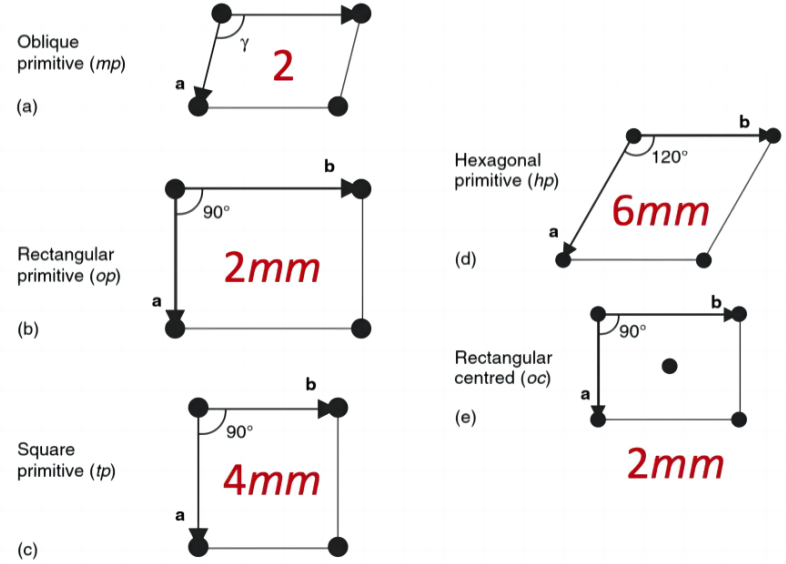
晶格(lattice):晶格是指晶体中原子排列的规律空间格架形式，是晶体的基本结构单位。以二维平面为例，下图是五种平面晶格：

点群是对称元素集合于一点，这些点构成了群，晶格是框架，把点构成的群嵌套在框架里就形成了空间群。

绘制空间群的基本步骤如下：

绘制其所位处的平面晶格；

在晶系内的每个节点内将点群置入；

寻找其他所有由于点群被引入而增添且隐含的对称要素

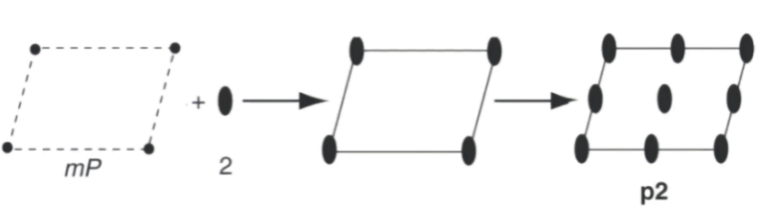
以二维斜晶格mP为例，若以2点群修饰二维晶系的每一个节点，即得到p2平面群：

实心圆表示2点群，空心圆代表位于一般位置的物体。在引入平移对称性的同时会向系统中引入新的对称要素。在引入2点群后，额外增加了位于形心和各边中点处的2重对称中心，因此将对称要素补全就得到了最后的p2对称性。

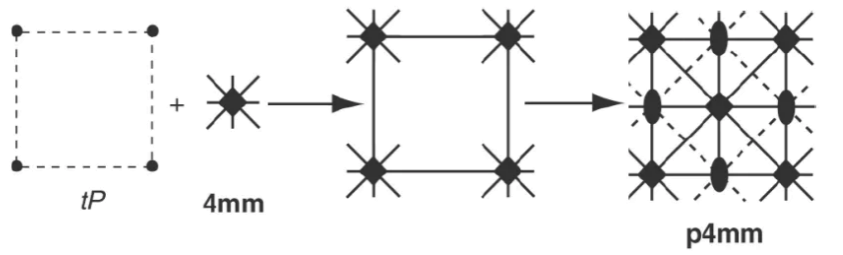
再举一个复杂一些的例子，向二维正方形晶格tp中引入 4mm点群，得到 p4mm平面群。

由于点群对称要素的引入，额外带来了位于各边中点处的2重对称中心、位于形心的4重对称性，和位于四个各边中点中的任意两点所确定的直线的滑移镜射。(实线表示对映对称，虚线表示滑移镜射面对称)

通过各种组合，一共可以形成17种平面群，230种空间群（包含平面群）。

10种平面点群＋5种平面晶格＝17种平面群

32种空间点群＋14种布拉威格子＝230种空间群

本节参考链接：晶体和晶体结构、平面群及空间群

代码

文本

2.图论

图 (graph) 是图论中最基本的概念之一，它是研究抽象对象之间相互联系规律的一个重要理论工具。一般采用顶点来指代抽象对象，而对象与对象之间的联系以及重要性用边来描述。图有很多的基本术语以及概念，如图的阶，子图，顶点以及度，边及其权重，路径与环，简单路径，有向图，无向图，有向无环图等。

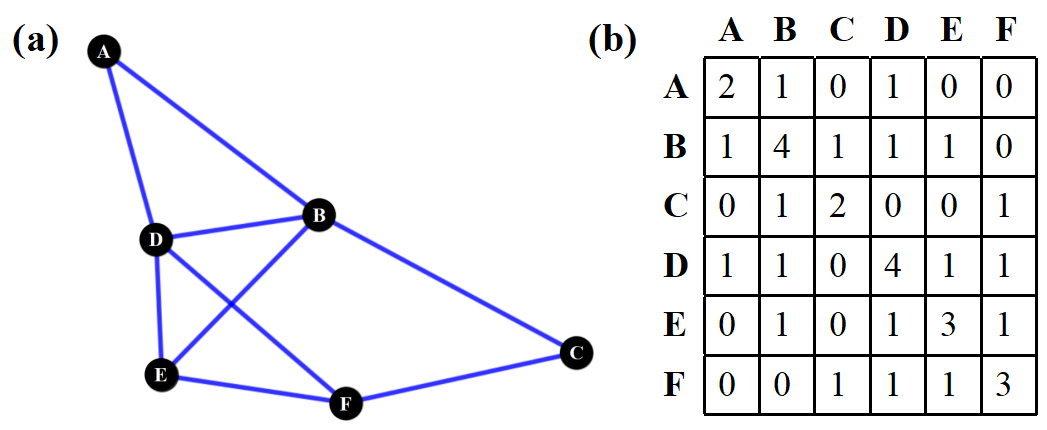
以一个无向图为例，图2.13(a)可以理解成A，B，C，D，E，F六人的家，这些家之间的路互相连通。这里的A，B，C，D，E，F六人就是图这一概念中所指的对象，称作顶点，它们的顶点集合（Vertices Set）V={A，B，C，D，E，F}；所有的路看作边，它们组成边集（Edges Set）E={AB，AD，BD，BE，BC，CF，FD，FE，ED}或者带权重的边集E={AB:1，AD:1，BD:1，BE:1，BC:1，CF:1，FD:1，FE:1，ED:1}；顶点E和边集V可以进一步简化成下图(a)所示的关系网络，称作图G={E,V}；也可以进一步表示成图(b)的矩阵形式。

图在描述晶体结构中的应用：原子(分子)，键长与成键关系的组合能够形成晶体结构。晶体材料的基元 (如：原子) 可以通过图的顶点集合 (Vertices Set) 来记录。基元之间的关联 (如：化学键) 则用边集 (Edges Set)。

晶体结构与图论有着很大的联系，有着代表性的一个工作是Xie等人设计了一个晶体图卷积神经网络(CGCNN)框架，直接从晶体中原子的连接中学习材料的性质，提供了一个通用的和可解释的晶体材料的表示。方法的主要思想是通过一个编码原子信息和原子间键合相互作用的晶体图来表示晶体结构，然后在该图上构建一个卷积神经网络，通过DFT计算数据训练自动提取最适合预测目标属性的表示。

图片来源：Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties

代码

文本

3.势能面

定义：势能面(Potential energy surface)是分子的能量与分子内原子的各向坐标有对应关系，由于原子和坐标的复杂性，势能面往往是一个高维函数。

势能面的极小值附近往往对应着一个较为稳定的晶体结构，因此通过势能面寻找稳定结构是晶体结构搜索最主要的方式之一。

代码

文本

三、晶体结构搜索算法

代码

文本

随机搜索：随机搜索的步骤非常简单：首先随机产生结构，然后进行结构弛豫（局域结构优化），最后比较结构的能量找出最小值点。这种方法很简单但是非常有效，已经成功预测出了许多新结构。最重要的一个限制条件是晶体的对称性。绝大多数已知的晶体都有较高的对称性，统计显示，空间群为 P1 的无机晶体占比小于 1%，因此采用随机搜索会做大量无用的工作。

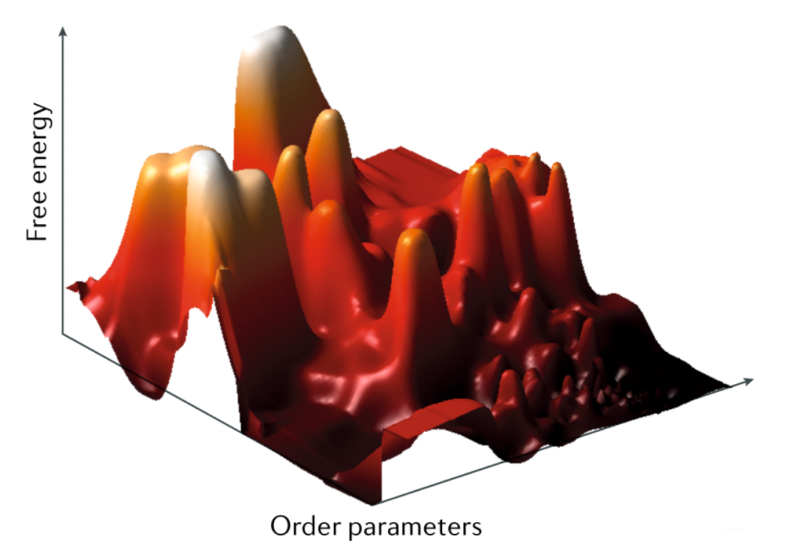
模拟退火：模拟退火是一种基于蒙特卡洛方法（Monte Carlo, MC）的启发式全局优化算法，其原理来自于材料的退火过程。在高温下，自由能面比势能面要平坦很多，因此高温下的动力学模拟容易跨过不同极小值间的势垒。随着温度降低，自由能面的能垒开始升高，动力学轨迹的分布范围变小，最后在零温时，系统收敛到基态。在自由能面上随机行走可以使用蒙特卡洛中的 Metropolis算法。进阶的通过不同方式寻找势能面的极小值点又进化出一些算法，如盆地跳跃、极小点跳跃等方法。

进化算法：进化算法是一种常用的启发式算法，它借鉴了自然界生物进化机制，进行高效的全局搜索。在进化算法中，每个解被视为一个个体，解集则是一个种群，目标函数值则对应个体的适应度。进化算法中的交叉操作促进个体间信息交流，变异操作探索未知的解空间，从优秀个体出发产生高质量的新个体。进化算法一方面通过交叉和变异操作产生新的解，另一方面通过“优胜劣汰”，去除适应度低的个体，保留优秀个体，使得整个种群向最优解靠拢。 进化算法只需要计算目标函数值，不需要计算导数，可以用来解决许多目标函数不光滑的优化问题。

进化算法的流程：首先随机生成初始的晶体结构；进行结构弛豫；从优化好的结构中选择焓值较低的结构作为父代个体，通过交叉和变异产生下一代结构；然后再进行结构弛豫。如此迭代演化，寻找势能面上的最小值点。

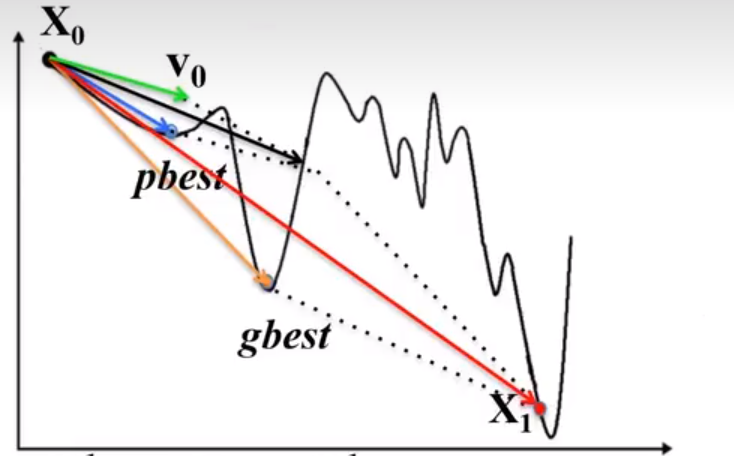
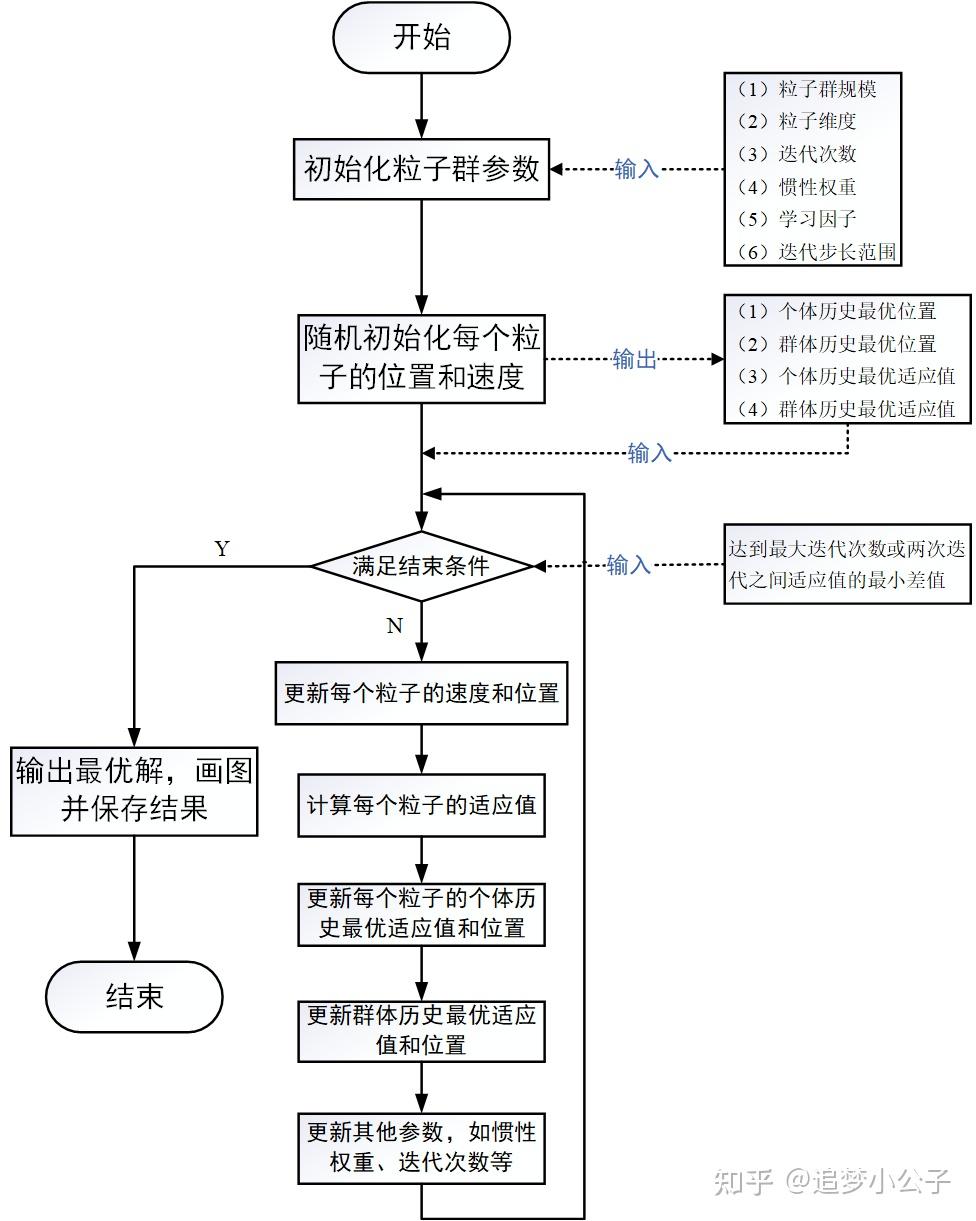
粒子群优化算法(PSO) :粒子群算法就参考了鸟群觅食的机制，鸟类通过共享信息来更新自己的认知，最终找到距离食物最近的点。它把每个潜在的解视为搜索空间中的一个粒子，粒子的适应度通过目标函数进行计算，粒子的飞行过程就是解的优化过程，

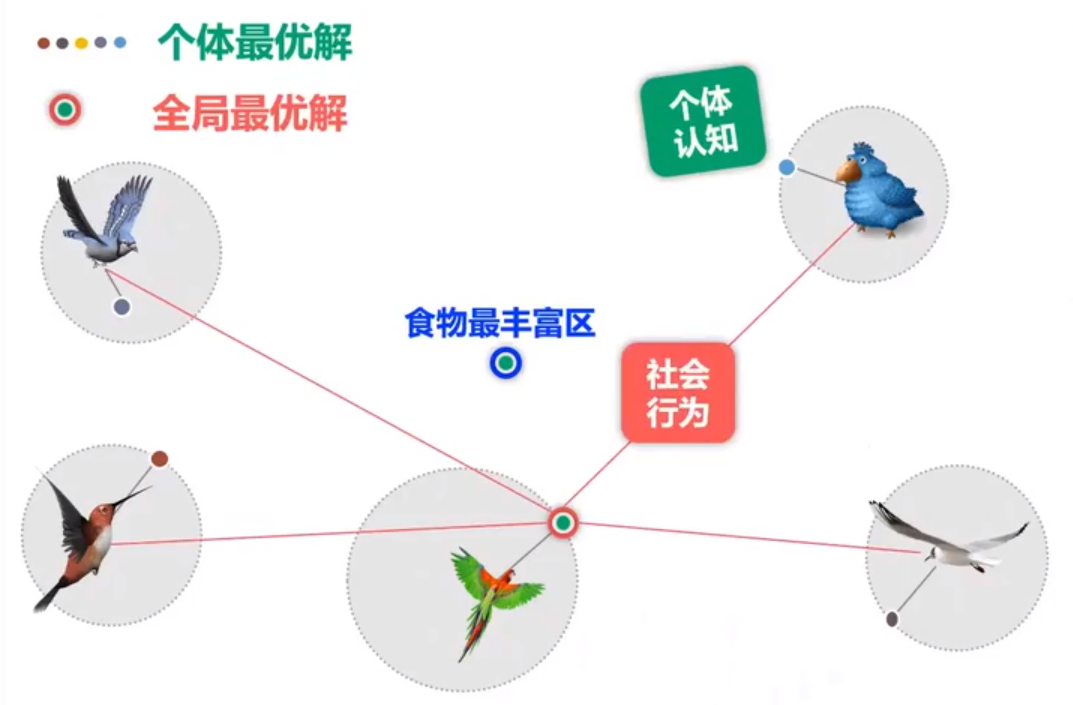
而结构搜索就是通过不断迭代更新寻找能量最低的点，粒子群优化算法具有参数设置少、全局寻优能力强、收敛速度快等优点。

代码

文本

下面是一个通过粒子群优化（PSO）算法寻找势能面极小值的一个python代码演示

代码

文本

我们假设寻找的势能面是Hölder table函数， $f (x, y) = - sin x cos y exp (1 - \frac{x ^{2} + y ^{2}}{π}), - 10 \leq x, y \leq 10$ 首先画一下这个函数

代码

文本

[1]

import numpy as np

import matplotlib.pyplot as plt

from mpl_toolkits.mplot3d import Axes3D

def draw_pic(X, Y, Z, z_max, title, z_min=0):

fig = plt.figure()

ax = Axes3D(fig)

fig.add_axes(ax)

ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=plt.cm.summer)

ax.set_zlim(z_min, z_max)

ax.set_title(title)

plt.show()

def get_X_AND_Y(X_min, X_max, Y_min, Y_max):

X = np.arange(X_min, X_max, 0.1)

Y = np.arange(Y_min, Y_max, 0.1)

X, Y = np.meshgrid(X, Y)

return X, Y

# Hölder table测试函数

def Holder_table(X_min = -10, X_max = 10, Y_min = -10, Y_max = 10):

X, Y = get_X_AND_Y(X_min, X_max, Y_min, Y_max)

Z = -np.abs(np.sin(X) * np.cos(Y) * np.exp(np.abs(1 - np.sqrt(X**2 + Y**2)/np.pi)))

return X, Y, Z, 0, "Hölder table function", -20

X, Y, Z, z_max, title, z_min = Holder_table()

draw_pic(X, Y, Z, z_max, title, z_min)

代码

文本

此函数有四个极小值点： $Min = ⎩ ⎨ ⎧ f (8.05502, 9.66459) f (- 8.05502, 9.66459) f (8.05502, - 9.66459) f (- 8.05502, - 9.66459) = - 19.2085 = - 19.2085 = - 19.2085 = - 19.2085$

代码

文本

接下来我们定义一个PSO算法，用来寻找该函数的极小值

代码

文本

图片来源：粒子群优化算法(Particle Swarm Optimization,PSO)的详细解读

代码

文本

[3]

import numpy as np

import random

def fit_fun(X): # 目标函数：Hölder table测试函数

return -np.abs(np.sin(X[0]) * np.cos(X[1]) * np.exp(np.abs(1 - np.sqrt(X[0] ** 2 + X[1] ** 2) / np.pi)))

class Particle:

# 初始化

def __init__(self, x_max, max_vel, dim):

self.__pos = [random.uniform(-x_max, x_max) for i in range(dim)] # 粒子的位置

self.__vel = [random.uniform(-max_vel, max_vel) for i in range(dim)] # 粒子的速度

self.__bestPos = [0.0 for i in range(dim)] # 粒子最好的位置

self.__fitnessValue = fit_fun(self.__pos) # 适应度函数值

def set_pos(self, i, value):

self.__pos[i] = value

def get_pos(self):

return self.__pos

def set_best_pos(self, i, value):

self.__bestPos[i] = value

def get_best_pos(self):

return self.__bestPos

def set_vel(self, i, value):

self.__vel[i] = value

def get_vel(self):

return self.__vel

def set_fitness_value(self, value):

self.__fitnessValue = value

def get_fitness_value(self):

return self.__fitnessValue

class PSO:

def __init__(self, dim, size, iter_num, x_max, max_vel, best_fitness_value=float('Inf'), C1=2, C2=2, W=1):

self.C1 = C1

self.C2 = C2

self.W = W

self.dim = dim # 粒子的维度

self.size = size # 粒子个数

self.iter_num = iter_num # 迭代次数

self.x_max = x_max

self.max_vel = max_vel # 粒子最大速度

self.best_fitness_value = best_fitness_value

self.best_position = [0.0 for i in range(dim)] # 种群最优位置

self.fitness_val_list = [] # 每次迭代最优适应值

# 对种群进行初始化

self.Particle_list = [Particle(self.x_max, self.max_vel, self.dim) for i in range(self.size)]

def set_bestFitnessValue(self, value):

self.best_fitness_value = value

def get_bestFitnessValue(self):

return self.best_fitness_value

def set_bestPosition(self, i, value):

self.best_position[i] = value

def get_bestPosition(self):

return self.best_position

# 更新速度

def update_vel(self, part):

for i in range(self.dim):

vel_value = self.W * part.get_vel()[i] + self.C1 * random.random() * (part.get_best_pos()[i] - part.get_pos()[i]) \

+ self.C2 * random.random() * (self.get_bestPosition()[i] - part.get_pos()[i])

if vel_value > self.max_vel:

vel_value = self.max_vel

elif vel_value < -self.max_vel:

vel_value = -self.max_vel

part.set_vel(i, vel_value)

# 更新位置

def update_pos(self, part):

for i in range(self.dim):

pos_value = part.get_pos()[i] + part.get_vel()[i]

part.set_pos(i, pos_value)

value = fit_fun(part.get_pos())

if value < part.get_fitness_value():

part.set_fitness_value(value)

for i in range(self.dim):

part.set_best_pos(i, part.get_pos()[i])

if value < self.get_bestFitnessValue():

self.set_bestFitnessValue(value)

for i in range(self.dim):

self.set_bestPosition(i, part.get_pos()[i])

def update(self):

for i in range(self.iter_num):

for part in self.Particle_list:

self.update_vel(part) # 更新速度

self.update_pos(part) # 更新位置

self.fitness_val_list.append(self.get_bestFitnessValue()) # 每次迭代完把当前的最优适应度存到列表

return self.fitness_val_list, self.get_bestPosition()

代码

文本

[5]

import matplotlib.pyplot as plt

import numpy as np

dim = 2 #我们设置x,y两个维度

size = 100 #粒子个数

iter_num = 500 #设置步长

x_max = 10

max_vel = 0.5 #最大速度

pso = PSO(dim, size, iter_num, x_max, max_vel)

fit_var_list, best_pos = pso.update()

print("最优位置:" + str(best_pos))

print("最优解:" + str(fit_var_list[-1]))

plt.plot(np.linspace(0, iter_num, iter_num), fit_var_list, c="r", alpha=0.5)

plt.show()

print()

最优位置:[-8.053869928557916, -9.664939165940977]
最优解:-19.208488317444303

代码

文本

注意！多次运行上面的代码你会发现每次找到的极小值不一致，这是由于算法陷入了极小值陷阱，无法找到整个函数的最小值，还有更先进的算法来优化这一现象，感兴趣的同学可以深入研究，这里就不多展示了。

代码

文本

四、机器学习力场

在原子尺度上计算材料性质时，有两类描述原子间相互作用的方法，分别是经验力场和第一性原理计算。

第一性原理计算能较准确地预测材料的物理性质，但是其目前主要用于处理含有数十到数百个原子的结构，对于更大的体系，计算量过大，还没有高效普适的处理方案。
经验力场是原子相互作用的简化模型，力场的形式来源于实验的经验公式或者量子力学的经典近似，其参数通过拟合实验数据或第一性原理计算结果得到。由于不考虑电子的相互作用，经验力场的速度比第一性原理计算要快几个数量级，因此可以处理很大的体系，但是经验力场的通用性和迁移性较差，一般的力场只能用于一种或几种化合物。即使是一些通用型的力场，其适用范围也局限在特定的领域，力场的相容性也是一大问题。
机器学习力场:机器学习的成功启发了材料计算领域的研究者，他们开始用机器学习算法改来进力场方法。通过搭建复杂的机器学习模型和运用恰当的训练方法，研究者已经构建了多种机器学习力场，其表现好于经验力场和半经验密度泛函方法。
相比于第一性原理计算和经验力场，机器学习力场有许多优势。首先，训练好的机器学习力场和第一性原理计算结果非常接近，平均到每个原子的能量误差可以低至数个毫电子伏。同时，机器学习力场的速度也非常快，可以用来模拟较大的体系，模拟时间也可以达到纳秒级别。此外，机器学习力场直接拟合原子构型和能量之间的函数关系，没有预设体系的性质，因此这是一种通用的方法，可以用于拟合不同材料以及它们复合结构的力场。

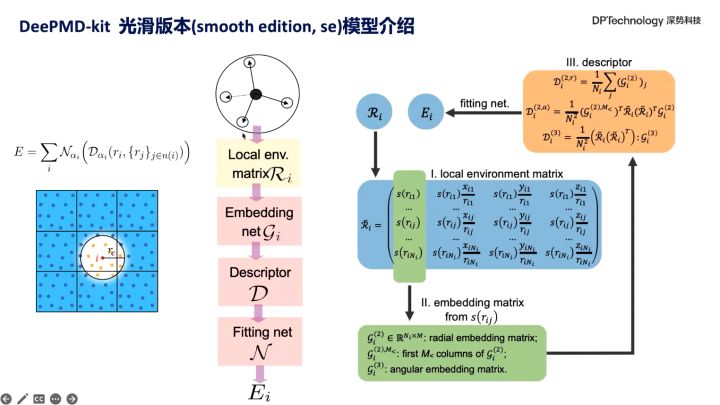
关于机器学习势详细的介绍可以参考Deepmodeling社区教程

代码

文本

五、结构搜索软件介绍

1.软件介绍

CALYPSO :CALYPSO（Crystal structure AnaLYsis by Particle Swarm Optimization）是一种有效的结构预测方法及其同名计算机软件。该方法只需要给定化合物的化学成分来预测给定外部条件（如压力）下的稳定或亚稳态结构，因此CALYPSO包可用于预测/确定晶体结构和设计多功能材料。
MAGUS : MAGUS（Machine learning And Graph theory assisted Universal structure Searcher）是南京大学孙建课题组开发的机器学习和图论辅助的晶体结构搜索方法，MAGUS是用Python和C++编写的晶体结构预测软件，支持三维，二维晶体，分子晶体，表面重构，团簇，受限空间等体系的定组分和变组分搜索。支持VASP，CASTEP，ORCA，MTP，NEP，DeepMD，gulp，lammps，XTB，ASE等接口，便于扩展。
USPEX ：USPEX（Universal Structure Predictor: Evolutionary Xtallography，俄语中“uspekh”的意思是“成功” - 暗示这种方法成功率高，并且可以产出许多有用的结果）是Oganov实验室从 2004 年以来开发的一种晶体结构预测方法和程序。晶体结构预测问题也由来已久，而且一直是理论晶体化学的重要核心问题 USPEX解决了这个问题，仅需给定材料的化学成分，就可以预测该材料体系在任意压力-温度条件下的潜在晶体结构。USPEX 提供与 VASP、SIESTA、GULP、DMACRYS、CP2k、QuantumEspresso、LAMMPS、ATK、MOPAC、FHI-aims、Gaussian 等程序的接口。
RG2 ：RG2是一款基于群论和商图的随机晶体结构搜索软件。将坐标空间中的晶体结构相变看作逻辑空间的商图相变，将表面重构转换为商图染色和商图相变相结合的问题来研究，在前期基于商图静态属性（点集，边集，环集等）发展起来的创新性方法中进一步引入商图染色策略和商图相变机制等动态属性来对晶体结构（结构相变，边缘/表面重构，界面和超晶格等）进行搜索。

2.快速上手

本文将以CALYPSO为例，在Bohrium Notebook中快速上手，链接：

代码

文本

六、结构搜索应用

代码

文本

Wang等人研究了锂（Li）在高压下的结构和电子性质，以及其相变和熔化行为。文章通过实验和理论计算相结合的方法，研究了锂在不同压力下的晶体结构、热力学稳定性和动态稳定性。文章还讨论了锂在高压下的熔化行为，并提出了一种新的加速搜索方法，用于寻找高压下锂的低能结构。论文地址：Data-driven prediction of complex crystal structures of dense lithium

代码

文本

在 $Cu_{2} N$ 的基态搜索采用了CALYPSO进行 $Cu_{2} N$ 的结构搜索，基于给定的化学成分有效地识别了基态和亚稳态结构。进行了单层Cu2N中棋盘格晶格的理论预测和实验实现。实验表明，单层 $Cu_{2} N$ 可以在众所周知的N/Cu（100）和N/Cu（111）体系中实现，这些体系以前被错误地认为是绝缘体。结合角度分辨光电发射光谱测量、第一性原理计算和紧密结合分析表明，这两个系统在费米能级附近都有棋盘格衍生的空穴袋。此外，单层 $Cu_{2} N$ 在空气和有机溶剂中具有优异的稳定性，这对进一步的器件应用至关重要。论文名称：Realization of a Two-Dimensional Checkerboard Lattice in Monolayer $Cu_{2} N$

代码

文本

Shao等人通过结构搜索，结合第一性原理计算，预测了FeGe拥有一个不寻常的混合电荷密度波--蜂窝电荷密度波。他们发现了一个2×2×1电荷密度波，它采用了Ge-蜂窝层的广义凯库勒扭曲的形式，而Fe-kagome层几乎保持不变研究分析表明，蜂窝状的广义凯库尔畸变很可能是由戈果美电子态的费米表面嵌套所驱动的。通过与扫描隧道显微镜获得的电子态密度数据的原子分布的匹配，进一步证实了预测的蜂窝型电荷密度波。论文地址：Intertwining of Magnetism and Charge Ordering in Kagome FeGe

代码

文本

Liu等人概念化了围绕金属氢化物超导体来实现这一目标的两个一般规则。规则1：金属骨架应由有效价为3的元素组成，以有效地提供电子给氢。规则2：对于对氢的最大化学压缩，金属离子的部分占用率应为∼0.4。在这些规则的指导下，基于第一性原理的方法，基于CALYPSO预测了一组新的氢化物超导体，包括 $CaHfH_{12}$ 的代表性样例，Tc为∼360K在300GPa下， $CaZrH_{12}$ ，Tc为∼290K在200GPa下。这些发现有望有助于预测在低压下新的高温氢化物超导体的发现。论文地址：Generic rules for achieving room-temperature superconductivity in ternary hydrides with clathrate structures

代码

文本

Pan等人利用晶体结构预测和从头算分子动力学模拟，发现氧化镁和水在超高压下可以再次反应，而 $Mg (OH)_{2}$ 在低压下分解。他们的研究结果表明，大量的水可以储存在地球内部深处的氧化镁岩石中，从而形成海王星质量的行星。基于分子动力学模拟，表明 $Mg_{2} O_{3} H_{2}$ , $MgO_{3} H_{4}$ , $MgO_{4} H_{6}$ 在压力-温度条件下表现出超电子行为，如在天王星和海王星的内部。此外，富含水的化合物 $MgO_{4} H_{6}$ 可能在早期地球内部稳定，因此可能成为早期地球的水库。他们的发现在缺乏探索的兆巴压力状态下，为太阳系中湿行星的内部和演化模型提供了约束。论文地址：Magnesium oxide-water compounds at megabar pressure and implications on planetary interiors

代码

文本

七、总结＆展望

代码

文本

利用好结构搜索的工具，我们可以做很多有趣的工作，上述的优秀的成果都是结构搜索+各自的研究方向碰撞出的火花。

代码

文本

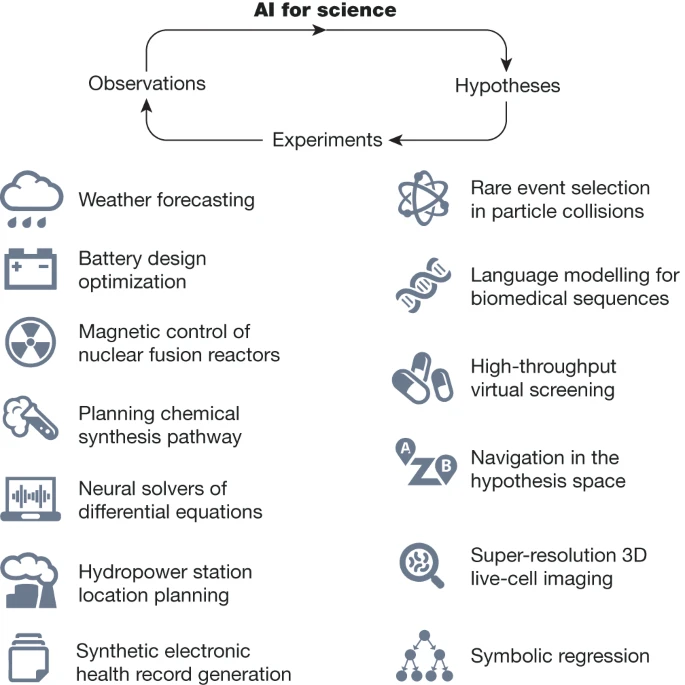
AI正越来越多地融入科学发现中，以增强和加速研究，帮助科学家生成假设、设计实验、收集和解释大规模数据，并获得传统科学无法获得的洞见。当今AI发展的黄金时代，AI对于Science来说必将是个强力的推进剂。我们需要形成计算思维来进行科学探索，同时恰到好处的应用AI这个工具，开创科学更加崭新的未来。

代码

文本

中文

AI4S

python

Tutorial

步道

中文AI4SpythonTutorial步道

已赞10

本文被以下合集收录

机器学习与DFT精华帖

gtang

更新于 2024-09-10

38 篇21 人关注

machine learning

hjchen

更新于 2024-02-26

16 篇7 人关注

AI for Science——漫步结构搜索

目录

一、AI for Science背景介绍

1.什么是AI for Sience？

2.AI for Science 助力科学的第四范式

二、结构搜索背景介绍

1.晶体与晶体结构

2.图论

3.势能面

三、晶体结构搜索算法

下面是一个通过粒子群优化（PSO）算法寻找势能面极小值的一个python代码演示

四、机器学习力场

五、结构搜索软件介绍

1.软件介绍

2.快速上手

六、结构搜索应用

七、总结＆展望