空间站广场

论文

Notebooks

比赛

课程

Apps

我的主页

我的Notebooks

我的论文库

我的足迹

我的工作空间

任务

节点

文件

数据集

镜像

项目

数据库

公开

扩散模型(DDPM)助力凝聚多肽的结构搜索

Diffusion Model

拉莫进洞

发布于 2023-09-07

推荐镜像 :ddpm:DDPM

推荐机型 :c12_m46_1 * NVIDIA GPU B

扩散模型(DDPM)助力凝聚多肽的结构搜索

选手简介

课题背景

算法背景

数据介绍

定义向前扩散过程（forward diffusion process）

定义向后扩散过程（backward diffusion process）

构建U-net解噪模型

1. 时间编码模块

2. 特征提取模块

3 自注意力模块

4 组归一化模块

5 组建U-net网络

训练模型

采样与后处理

总结与展望

小组分工

扩散模型(DDPM)助力凝聚多肽的结构搜索

代码

文本

选手简介

代码

文本

©️ Copyright 2023 @ Authors
作者：胡家鸣 📨 杨珺婷 📨
院校：西湖大学工学院
**特别鸣谢** 西湖大学工学院助理研究员汪嘉琪提供了分子动力学数据用于本案例
参加过什么比赛：第三届 DeepModeling Hackathon 比赛
获得过什么奖项 : 第三届 DeepModeling Hackathon 大赛中获得AI4Lifescience赛道二等奖
推荐环境：
共享协议：本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。

代码

文本

课题背景

代码

文本

在生物系统中，单个大分子可以自组装成各种各样的超结构，在生命系统中发挥作用。控制此类系统形成的大多数分子相互作用是非共价的，其可逆性赋予了分子结构对外部刺激做出反应的能力。其中，蛋白质构成了一类特别多样化的自组装材料。举例来说，细胞运动和对表面的牵引力受到细胞骨架蛋白自我组装能力的显著调节；这些蛋白质的可逆自组装能够严格调节细胞的伸展和收缩，从而促进运动；其组装体网络还为许多活性过程提供能量，包括细胞迁移、细胞内内吞囊泡和其他膜结合细胞器的运动，以及特定细菌和病毒病原体的细胞间运输。

在天然和合成蛋白质自组装的研究中，人们发现尽管自然界中功能材料的构建单元通常是具有多达几百个氨基酸残基的蛋白质序列，但更短的氨基酸序列也可以表现出极其复杂的自组装行为。为此，人们通过仿生肽序列（包括肽两亲物、脂肽以及与其他分子的缀合物），来设计、预测和合成可自组装的多功能分子，形成了蓬勃发展的肽仿生领域，旨在设计出具有与天然产品相当或更好功能的合成材料。

在众多肽仿生自组装材料中，肽水凝胶由于其生物相容性、低免疫原性和与细胞外基质的相似性，引起了人们的极大关注。水凝胶是由固定水的自组装基质形成的软材料，研究人员认为水凝胶能够良好地模仿很多自然系统，如水母体、角膜、细胞核中浓缩的染色质等。到目前为止，肽水凝胶已广泛应用，包括材料科学、生物医学和半导体。然而，目前的设计能力尚达不到对新型肽水凝胶日益增长的需求，因为目前使用的技术仍然依赖于源自天然蛋白质的氨基酸序列、肽领域的专家知识或偶然的实验室发现。因此，从头肽水凝胶设计和准确的水凝胶形成预测对于建设水凝胶多肽的设计数据库至关重要。

在此方面，粗粒化分子动力学(CGMD)已被广泛用于模拟肽的自组装。然而，由于多肽设计空间十分巨大，对于n-肽来说，每个氨基酸残基都有20余种选择，则仅肽链序列就有 $2 0^{n}$ 种，且还有丰富的二级、三级结构，因此直接进行CGMD模拟十分昂贵且低效。

为此，基于已知的多肽水凝胶，利用机器学习的方法预测生成新的凝聚多肽结构，成为一个十分有潜力的研究方向。

代码

文本

算法背景

代码

文本

材料结构预测类任务的主要困难在于寻找稳定的结构。虽然材料结构的设计空间非常之大（可以想像，一个材料通常由多个原子构成，而每个原子又都可以放在三维空间的各个位置），但能够稳定存在的材料结构只是其中的很小一部分，即被限制在所有可能的排列的低维子空间内，这主要包括以下要求：1）原子坐标必须处于量子力学定义的局部能量最小值；2）全局稳定性还要求结构遵守各种原子类型之间复杂而独特的键合偏好；3）对跨越周期边界的3D结构与相互作用进行编码，并满足排列、平移、旋转和周期不变量。目前，机器学习用于对于3D周期材料的生成预测已有多种解决方案，包括但不限于以下分类：

材料图表示学习（Material graph representation learning）。图神经网络在材料性能预测中发挥了重要作用。Xie, Grossman（2018）首次将它们应用于周期材料的表征学习，后来通过包括Schutt等人在内的许多研究得到了加强（2018）。
量子力学搜索（Quantum mechanical search）。预测未知材料的结构需要非常昂贵的随机搜索和QM模拟(Oganov等人, 2019). 现有技术的方法包括随机采样（Pickard&Needs，2011）、进化算法等，但它们通常成功率较低，即使在相对较小的问题上也需要大量计算。
材料生成模型（Material generative models）。已有的材料生成模型主要关注两种不同的方法。第一种方法将材料视为3D体素图像，但将图像解码回原子类型和坐标的过程往往导致有效性低，并且模型不是旋转不变的（Hoffmann等人，2019；Noh等人，2019年；Court等人，2020；Long等人，2021）。第二种方法直接将原子坐标、类型和晶格编码为向量（Ren等人，2020年；Kim等人，2020；Zhao等人，2021），但模型通常不会对任何欧几里德变换保持不变。另一种相关方法是从QM力训练力场，然后应用学习到的力场，通过最小化能量来产生稳定的材料，这种方法在概念上类似于扩散模型的解码器，但它需要额外的、昂贵的力场数据。
分子构象的产生和蛋白质折叠（Molecular conformer generation and protein folding）。通过扩散过程生成3D原子结构的解码器与用于生成分子构象异构体的扩散模型密切相关（Shi等人，2021；Xu等人，2021）。扩散模型不依赖于像分子图这样的中间表示，而是直接逐个原子的生成3D分子。

在众多算法模型中，扩散模型(Denoising Diffusion Probabilistic Models, DDPM)是近两年兴起的一种生成型人工智能模型，在图片生成等领域与传统的生成变分自编码器（Variational autoencoder，VAE）、生成对抗性网络（Generative adversarial network，GAN）相比有着不俗的性能。基于E(3)等变的图表示的扩散模型等已经在小分子上显示出有效性。

目前，上述各类方法主要针对无机晶体、蛋白质等体系，针对凝聚多肽（多肽水凝胶）的结构预测工作尚未见诸报道。本课题旨在基于前人工作，使用DDPM学习Gromacs分子动力学计算得到的多肽结构数据，构建其2D投影表示，利用DDPM网络进行学习并预测生成更多稳定的凝聚多肽体系。

主要参考：

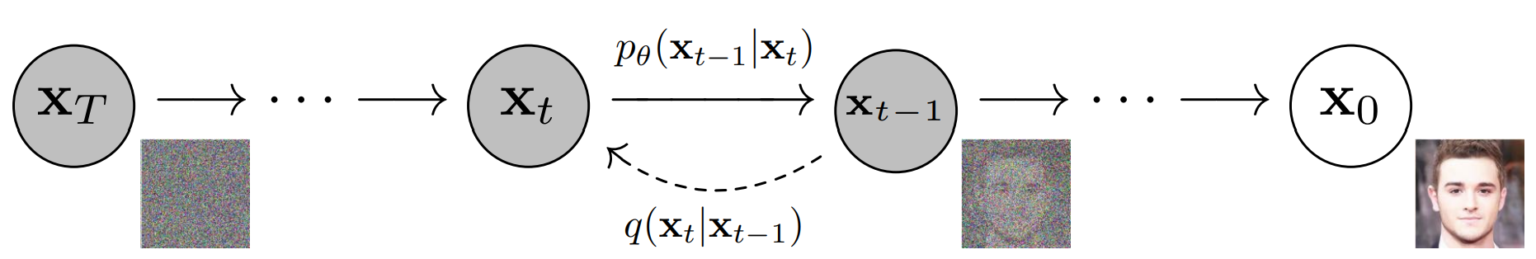
Diffusion process

代码

文本

数据介绍

代码

文本

采用的数据是约16000个四肽水溶液体系的结构（实际训练中采样800～2000个）。每个结构都经过粗粒化分子动力学(CGMD)优化弛豫。其中“粗粒化“是指分子动力学力场采用了Martini粗粒化分子动力学力场，它一般将四个重原子用一个粒子（bead）代替；环状分子中两到三个重原子用一个粒子代替；四个水分子用一个粒子代替，若考虑可极化作用则用三个粒子代替，下文中我们所称的”原子“就是这些粗粒化的粒子bead。20种常见氨基酸的粗粒化表示如图

计算的流程如下图，先生成300个四肽短肽链，随机分布在格子中，然后充满水分子，再在常温下进行分子动力学模拟，最终得到弛豫好的结构，去除水分子、离子后即可得到水溶相四肽的结构，以Gromacs软件包的结构文件.gro格式存储。

下面展示了一些优化好的结构示例，绝大部分结构经过弛豫后，四肽小分子都会发生团聚现象，因而也称为凝聚多肽。可以从这些.gro文件获取凝聚多肽的2D投影表示（见另一篇Bohrium notebook)，它具有图片的格式，可以直接输入DDPM进行训练。

值得注意的是，虽然这16000个多肽水溶液结构中，有的多肽是分散的、有的是凝聚的，但重点是它们都是经过可靠的分子动力学优化弛豫而来，因此可以认为都是稳定合理、符合物理规律的结构。这对于我们关注的生成任务，即让扩散模型去学习“一个稳定的多肽水溶液到底长什么样”从而使它能“自己设计”新的稳定的多肽水溶液体系，是最重要的。

代码

文本

[1]

import math

from inspect import isfunction

from functools import partial

import matplotlib.pyplot as plt

from tqdm.auto import tqdm

from einops import rearrange

import numpy as np

import torch

from torch import nn, einsum

import torch.nn.functional as F

代码

文本

定义向前扩散过程（forward diffusion process）

代码

文本

向前扩散过程即按照一定顺序（扩散时间步）依次向图片添加弱高斯噪声。对某个时间步 $t - 1$ ，被加噪的图片为 $X_{t - 1}$ ，则 $X_{t}$ 即为 $X_{t - 1}$ 加上一个方差为 $β_{t - 1} I$ ( $I$ 为单位张量)、均值为 $α_{t - 1} X_{t - 1}$ ( $α_{t - 1} = 1 - β_{t - 1}$ )的条件高斯分布（conditional Gaussian distribution），记为 $q (X_{t + 1} ∣ X_{t})$ 。对于扩散时间步 $t = 0, 1, 2, ..., T$ ，设置 $β_{t}$ 的分布（variance schedules）对神经网络学习逆向解噪很重要。实际计算中可以通过标准高斯分布$\mathbf{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$计算得到$X_t = \sqrt{1 - \beta_t} X_{t-1} + \sqrt{\beta_t} \mathbf{\epsilon}$。根据DDPM原文的设置，对于数值范围 $[- 1, 1]$ 的图片数据，我们设置 $β_{0} = 1 0^{- 4}$ ， $β_{T} = 0.02$ ， $T = 1000$ ，并采用线性方差序列(linear schedule)。较大的 $T$ 意味着更精细的扩散时间步划分，有助于减小生成图片的信噪比。

代码

文本

[2]

timesteps = 1000

def linear_beta_schedule(timesteps):

beta_start = 1e-4

beta_end = 0.02

return torch.linspace(beta_start, beta_end, timesteps)

# define schedule

betas = linear_beta_schedule(timesteps=timesteps)

alphas = 1. - betas

代码

文本

由于高斯分布的优良性质，从 $t = 0$ 扩散到 $t = t^{'}$ 并不需要真的依次计算 $q (X_{1} ∣ X_{0}), q (X_{2} ∣ X_{1}) ... q (X_{t^{'}} ∣ X_{t^{'} - 1})$ ，因为多个高斯分布的乘积还是高斯分布，所以这一过程 $q (X_{t^{'}} ∣ X_{0})$ 等价于一个均值为 $\overset{α_{t}}{ˉ} X_{0}$ ，方差为 $(1 - \overset{α}{ˉ}_{t}) I$ 的高斯分布 $q (X_{t} ∣ X_{0}) = N (X_{t}; \overset{α}{ˉ}_{t} X_{0}, (1 - \overset{α}{ˉ}_{t}) I)$

代码

文本

[3]

alphas_cumprod = torch.cumprod(alphas, axis=0)

alphas_cumprod_prev = F.pad(alphas_cumprod[:-1], (1, 0), value=1.0)

sqrt_recip_alphas = torch.sqrt(1.0 / alphas)

#q(x_t | x_{t-1})

sqrt_alphas_cumprod = torch.sqrt(alphas_cumprod)

sqrt_one_minus_alphas_cumprod = torch.sqrt(1. - alphas_cumprod)

#q(x_{t-1} | x_t, x_0)

posterior_variance = betas * (1. - alphas_cumprod_prev) / (1. - alphas_cumprod)

代码

文本

有了以上定义，我们可以定义q_sample函数从初始无噪声的图片x_start得到任意时间步t的噪声图像

代码

文本

[4]

def extract(a, t, x_shape):

batch_size = t.shape[0]

out = a.gather(-1, t.cpu())

return out.reshape(batch_size, *((1,) * (len(x_shape) - 1))).to(t.device)

# forward diffusion

def q_sample(x_start, t, noise=None):

if noise is None:

noise = torch.randn_like(x_start)

sqrt_alphas_cumprod_t = extract(sqrt_alphas_cumprod, t, x_start.shape)

sqrt_one_minus_alphas_cumprod_t = extract(

sqrt_one_minus_alphas_cumprod, t, x_start.shape

)

return sqrt_alphas_cumprod_t * x_start + sqrt_one_minus_alphas_cumprod_t * noise

代码

文本

让我们通过一个例子来看看高丝噪声对图片的影响，可以看到在第200步噪声时，图片已经几乎无法辨认。

代码

文本

[5]

from torchvision.transforms import Compose, ToTensor, Lambda, ToPILImage, CenterCrop, Resize

import matplotlib.pyplot as plt

import matplotlib.image as mpimg

reverse_transform = Compose([

Lambda(lambda t: (t + 1) / 2),

Lambda(lambda t: t.permute(1, 2, 0)), # CHW to HWC

Lambda(lambda t: t * 255.),

Lambda(lambda t: t.numpy().astype(np.uint8)),

ToPILImage(),

])

def get_noisy_image(x_start, t):

x_noisy = q_sample(x_start, t=t)

noisy_image = reverse_transform(x_noisy.squeeze())

return noisy_image

x_0 = torch.tensor(mpimg.imread('6 2.png'))

plt.imshow(x_0)

plt.show()

for i in [5, 199]:

t = torch.tensor([i])

x_t = get_noisy_image(rearrange(x_0, 'h w c -> c h w'), t)

plt.imshow(x_t)

plt.title('t='+str(i))

plt.show()

代码

文本

定义向后扩散过程（backward diffusion process）

代码

文本

根据对向前扩散过程的讨论，如果我们能训练一个神经网络denoise_model，它知道每一步添加的噪声“长什么样”，那就可以通过它一步步从完全无序的高斯噪声中还原出一副有序的图片，我们称之为向后扩散过程，记为 $p (X_{t - 1} ∣ X_{t})$ . 因此，评价denoise_model的好坏，就是要看它预测的噪声predicted_noise和实际向前扩散的噪声x_noisy之间的差异是否够小，据此我们可以定义训练神经网络的损失函数p_loss如下

代码

文本

[6]

def p_losses(denoise_model, x_start, t, noise=None, loss_type="l1"):

if noise is None:

noise = torch.randn_like(x_start)

x_noisy = q_sample(x_start=x_start, t=t, noise=noise)

predicted_noise = denoise_model(x_noisy, t)

if loss_type == 'l1':

loss = F.l1_loss(noise, predicted_noise)

elif loss_type == 'l2':

loss = F.mse_loss(noise, predicted_noise)

elif loss_type == "huber":

loss = F.smooth_l1_loss(noise, predicted_noise)

else:

raise NotImplementedError()

return loss

代码

文本

类似地，我们可以像向前扩散函数q_sample类似地定义向后扩散函数p_sample，只是此时扩散的均值和方差都由我们要训练的神经网络model预测

代码

文本

[7]

@torch.no_grad()

def p_sample(model, x, t, t_index):

betas_t = extract(betas, t, x.shape)

sqrt_one_minus_alphas_cumprod_t = extract(

sqrt_one_minus_alphas_cumprod, t, x.shape

)

sqrt_recip_alphas_t = extract(sqrt_recip_alphas, t, x.shape)

# Equation 11 in the paper

# Use our model (noise predictor) to predict the mean

model_mean = sqrt_recip_alphas_t * (

x - betas_t * model(x, t) / sqrt_one_minus_alphas_cumprod_t

)

if t_index == 0:

return model_mean

else:

posterior_variance_t = extract(posterior_variance, t, x.shape)

noise = torch.randn_like(x)

# Algorithm 2 line 4:

return model_mean + torch.sqrt(posterior_variance_t) * noise

# Algorithm 2 but save all images:

@torch.no_grad()

def p_sample_loop(model, shape):

device = next(model.parameters()).device

b = shape[0]

# start from pure noise (for each example in the batch)

img = torch.randn(shape, device=device)

imgs = []

for i in tqdm(reversed(range(0, timesteps)), desc='sampling loop time step', total=timesteps):

img = p_sample(model, img, torch.full((b,), i, device=device, dtype=torch.long), i)

imgs.append(img.cpu().numpy())

return imgs

@torch.no_grad()

def sample(model, image_size, batch_size=16, channels=3):

return p_sample_loop(model, shape=(batch_size, channels, image_size, image_size))

代码

文本

构建U-net解噪模型

代码

文本

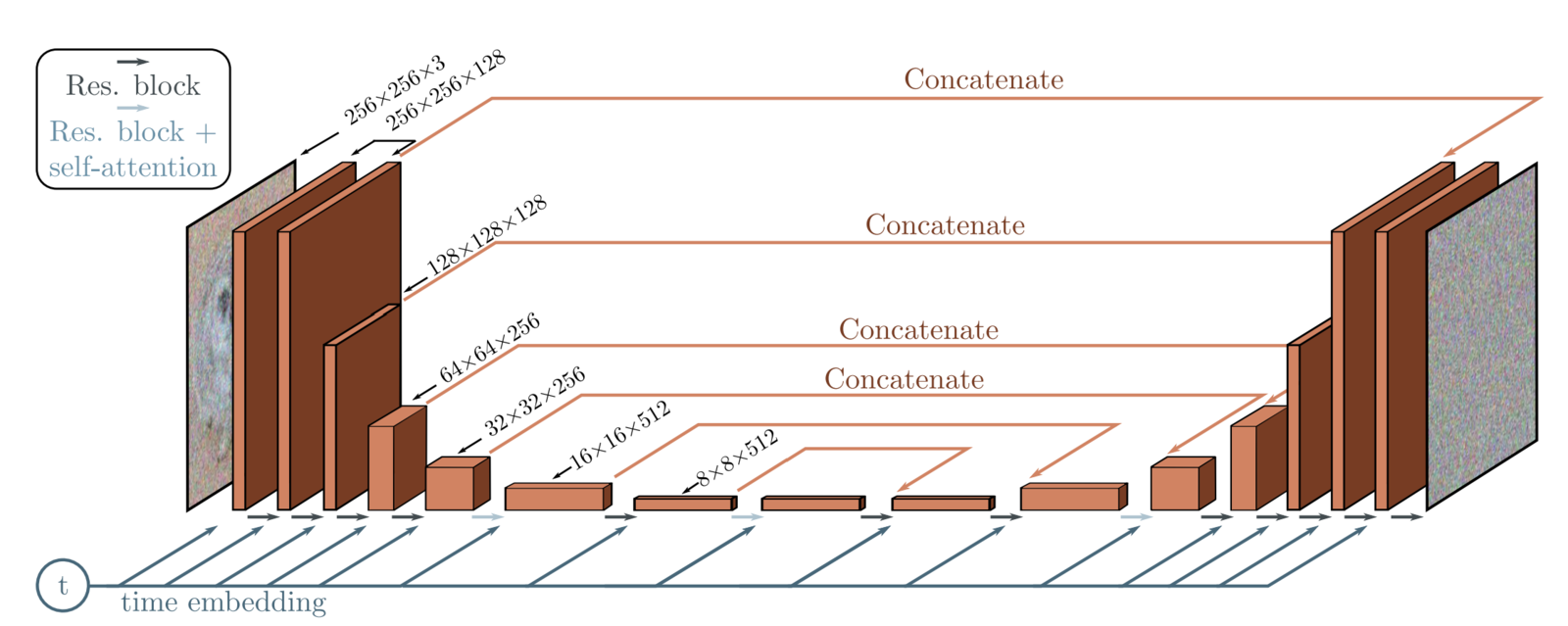
在DDPM中，作者采用一种能够自编码-解码的“U形”神经网络U-net来学习如何逆向解噪。U-net的输入是加噪时间步的和对应的图片，输出的解噪后的图片和解噪时间步。它由5个部分组成：

编码模块(Encoder blocks)：构成网络的前半部分，共3～4层，每一层都包括一系列，它能够“取其精华、去其糟粕”，将一张图片不断“压缩”，提取特征；
瓶颈模块(Bottleneck blocks)：连接编码模块和解码模块；
解码模块(Decoder blocks)：构成网络的后半部分，于编码模块层数相同，将特征图不断“扩容”读取特征；
自注意力模块(Self attention modules)
时间编码模块(Sinusoidal time embeddings)

代码

文本

1. 时间编码模块

由于神经网络的参数在时间上是共享的（噪声水平），受Transformer的启发，DDPM采用正弦位置嵌入(Sinusoidal Position Embeddings)来编码扩散 $t$ ，这使得神经网络“知道”它在哪个特定的时间步长（噪声水平）下运行。

具体来说，对于某个时刻 $t = t_{k}$ , 其 $d$ 维位置向量 $p_{k} = (p_{k, 0}, p_{k, 1} ..., p_{k, 2 i}, p_{k, 2 i + 1}, ..., p_{k, d})$ 中的各分量 $p_{k, 2 i}, p_{k, 2 i + 1}$ 分别为

$p_{k, 2 i} = sin (\frac{k}{1000 0 ^{2 i / d}}), p_{k, 2 i + 1} = cos (\frac{k}{1000 0 ^{2 i / d}})$

代码

文本

[8]

class SinusoidalPositionEmbeddings(nn.Module):

def __init__(self, dim):

super().__init__()

self.dim = dim

def forward(self, time):

device = time.device

half_dim = self.dim // 2

embeddings = math.log(10000) / (half_dim - 1)

embeddings = torch.exp(torch.arange(half_dim, device=device) * -embeddings)

embeddings = time[:, None] * embeddings[None, :]

embeddings = torch.cat((embeddings.sin(), embeddings.cos()), dim=-1)

return embeddings

代码

文本

为了直观理解，我们可以看看embedding向量具体长什么样。

代码

文本

[9]

sin_emb = SinusoidalPositionEmbeddings(200)

time = torch.arange(100)

p_time = sin_emb.forward(time).numpy()

print(p_time.shape)

fig, (ax1,ax2) = plt.subplots(2,1,num=2)

plt.subplots_adjust(hspace=0.5)

for t in [30,50,99]:

ax1.plot(p_time[t],label='$t_k=$'+str(t))

ax1.set_xlabel('Image Position i')

ax1.set_ylabel('$p_{k,i}$')

ax1.legend()

for i in [3,9,40]:

ax2.plot(p_time[:,i],label='Position i='+str(i))

ax2.set_xlabel('Diffusion time $t_k$')

ax2.set_ylabel('$p_{k,i}$')

ax2.legend()

plt.show()

代码

文本

首先定义两个辅助函数

代码

文本

[10]

def exists(x):

return x is not None

def default(val, d):

if exists(val):

return val

return d() if isfunction(d) else d

代码

文本

2. 特征提取模块

接着定义U-net的核心：特征提取模块，其中包括：

"升级版卷积模块“ConvNext
下/上采样模块：分别用2D卷积操作nn.Conv2D和转置卷积操作nn.ConvTranspose2d实现。传统的卷积操作能够不断提取图片的特征进行编码，而通过转职卷积操作“解释”特征进行解码。前者通过下采样函数Downsample调用pytorch的实现，后者通过上采样函数Upsample调用pytorch的2D[]实现。对于不熟悉卷积的同学不要紧，这里和这两张动图都可以直观展示：

Downsample. Upsample.

代码

文本

[11]

class Residual(nn.Module):

def __init__(self, fn):

super().__init__()

self.fn = fn

def forward(self, x, *args, **kwargs):

return self.fn(x, *args, **kwargs) + x

def Upsample(dim):

return nn.ConvTranspose2d(dim, dim, 4, 2, 1)

def Downsample(dim):

return nn.Conv2d(dim, dim, 4, 2, 1)

class Block(nn.Module):

def __init__(self, dim, dim_out, groups = 8):

super().__init__()

self.proj = nn.Conv2d(dim, dim_out, 3, padding = 1)

self.norm = nn.GroupNorm(groups, dim_out)

self.act = nn.SiLU()

def forward(self, x, scale_shift = None):

x = self.proj(x)

x = self.norm(x)

if exists(scale_shift):

scale, shift = scale_shift

x = x * (scale + 1) + shift

x = self.act(x)

return x

class ConvNextBlock(nn.Module):

"""https://arxiv.org/abs/2201.03545"""

def __init__(self, dim, dim_out, *, time_emb_dim=None, mult=2, norm=True):

super().__init__()

self.mlp = (

nn.Sequential(nn.GELU(), nn.Linear(time_emb_dim, dim))

if exists(time_emb_dim)

else None

)

self.ds_conv = nn.Conv2d(dim, dim, 7, padding=3, groups=dim)

self.net = nn.Sequential(

nn.GroupNorm(1, dim) if norm else nn.Identity(),

nn.Conv2d(dim, dim_out * mult, 3, padding=1),

nn.GELU(),

nn.GroupNorm(1, dim_out * mult),

nn.Conv2d(dim_out * mult, dim_out, 3, padding=1),

)

self.res_conv = nn.Conv2d(dim, dim_out, 1) if dim != dim_out else nn.Identity()

def forward(self, x, time_emb=None):

h = self.ds_conv(x)

if exists(self.mlp) and exists(time_emb):

assert exists(time_emb), "time embedding must be passed in"

condition = self.mlp(time_emb)

h = h + rearrange(condition, "b c -> b c 1 1")

h = self.net(h)

return h + self.res_conv(x)

代码

文本

3 自注意力模块

自注意力模块(Self attention block)是著名的Transformer架构的组成部分, DDPM采用了两个attention的变体:regular multi-head self-attention 和linear attention variant. 后者的内存和计算时间需求随着序列长度线性增长，因而比平方增长的常规attention更加高效。

代码

文本

[12]

class Attention(nn.Module):

def __init__(self, dim, heads=4, dim_head=32):

super().__init__()

self.scale = dim_head**-0.5

self.heads = heads

hidden_dim = dim_head * heads

self.to_qkv = nn.Conv2d(dim, hidden_dim * 3, 1, bias=False)

self.to_out = nn.Conv2d(hidden_dim, dim, 1)

def forward(self, x):

b, c, h, w = x.shape

qkv = self.to_qkv(x).chunk(3, dim=1)

q, k, v = map(

lambda t: rearrange(t, "b (h c) x y -> b h c (x y)", h=self.heads), qkv

)

q = q * self.scale

sim = einsum("b h d i, b h d j -> b h i j", q, k)

sim = sim - sim.amax(dim=-1, keepdim=True).detach()

attn = sim.softmax(dim=-1)

out = einsum("b h i j, b h d j -> b h i d", attn, v)

out = rearrange(out, "b h (x y) d -> b (h d) x y", x=h, y=w)

return self.to_out(out)

class LinearAttention(nn.Module):

def __init__(self, dim, heads=4, dim_head=32):

super().__init__()

self.scale = dim_head**-0.5

self.heads = heads

hidden_dim = dim_head * heads

self.to_qkv = nn.Conv2d(dim, hidden_dim * 3, 1, bias=False)

self.to_out = nn.Sequential(nn.Conv2d(hidden_dim, dim, 1),

nn.GroupNorm(1, dim))

def forward(self, x):

b, c, h, w = x.shape

qkv = self.to_qkv(x).chunk(3, dim=1)

q, k, v = map(

lambda t: rearrange(t, "b (h c) x y -> b h c (x y)", h=self.heads), qkv

)

q = q.softmax(dim=-2)

k = k.softmax(dim=-1)

q = q * self.scale

context = torch.einsum("b h d n, b h e n -> b h d e", k, v)

out = torch.einsum("b h d e, b h d n -> b h e n", context, q)

out = rearrange(out, "b h c (x y) -> b (h c) x y", h=self.heads, x=h, y=w)

return self.to_out(out)

代码

文本

4 组归一化模块

在卷积/attention层之间还加入了组归一化(group normalization)

代码

文本

[13]

class PreNorm(nn.Module):

def __init__(self, dim, fn):

super().__init__()

self.fn = fn

self.norm = nn.GroupNorm(1, dim)

def forward(self, x):

x = self.norm(x)

return self.fn(x)

代码

文本

5 组建U-net网络

定义了各组成模块后，我们根据以下顺序依次搭建U-net网络。网络的输入是一个训练图片batch(batch_size, num_channels, height, width)+噪声(batch_size, 1) ，输出用于解噪的逆噪声(batch_size, num_channels, height, width)。网络结构为：

输入：加噪图片和加噪时间步被送入一个卷积层，其中加噪时间步转换为对应的embedding向量
编码：经过多层编码模块进行编码。每一个编码模块包含2个ConvNeXT模块 + 1个组归一化 + 1个自注意力模块 + 残差连接 + 下采样模块
瓶颈：“平级处理”，由1个卷积层+1个attention层+1个卷积层构成
解码：经过多层解码模块进行编码。每一个编码层包含2个ConvNeXT模块 + 1个组归一化模块 + 1个自注意力模块 + 残差连接 + 上采样模块
输出：ConvNeXT模块+一个卷积层输出

代码

文本

[14]

class Unet(nn.Module):

def __init__(

self,

dim,

init_dim=None,

out_dim=None,

dim_mults=(1, 2, 4, 8),

channels=3,

with_time_emb=True,

resnet_block_groups=8,

use_convnext=True,

convnext_mult=2,

super().__init__()

# determine dimensions

self.channels = channels

init_dim = default(init_dim, dim // 3 * 2)

self.init_conv = nn.Conv2d(channels, init_dim, 7, padding=3)

dims = [init_dim, *map(lambda m: dim * m, dim_mults)]

in_out = list(zip(dims[:-1], dims[1:]))

if use_convnext:

block_klass = partial(ConvNextBlock, mult=convnext_mult)

else:

block_klass = partial(ResnetBlock, groups=resnet_block_groups)

# time embeddings

if with_time_emb:

time_dim = dim * 4

self.time_mlp = nn.Sequential(

SinusoidalPositionEmbeddings(dim),

nn.Linear(dim, time_dim),

nn.GELU(),

nn.Linear(time_dim, time_dim),

)

else:

time_dim = None

self.time_mlp = None

# layers

self.downs = nn.ModuleList([])

self.ups = nn.ModuleList([])

num_resolutions = len(in_out)

for ind, (dim_in, dim_out) in enumerate(in_out):

is_last = ind >= (num_resolutions - 1)

self.downs.append(

nn.ModuleList(

[

block_klass(dim_in, dim_out, time_emb_dim=time_dim),

block_klass(dim_out, dim_out, time_emb_dim=time_dim),

Residual(PreNorm(dim_out, LinearAttention(dim_out))),

Downsample(dim_out) if not is_last else nn.Identity(),

]

)

mid_dim = dims[-1]

self.mid_block1 = block_klass(mid_dim, mid_dim, time_emb_dim=time_dim)

self.mid_attn = Residual(PreNorm(mid_dim, Attention(mid_dim)))

self.mid_block2 = block_klass(mid_dim, mid_dim, time_emb_dim=time_dim)

for ind, (dim_in, dim_out) in enumerate(reversed(in_out[1:])):

is_last = ind >= (num_resolutions - 1)

self.ups.append(

nn.ModuleList(

[

block_klass(dim_out * 2, dim_in, time_emb_dim=time_dim),

block_klass(dim_in, dim_in, time_emb_dim=time_dim),

Residual(PreNorm(dim_in, LinearAttention(dim_in))),

Upsample(dim_in) if not is_last else nn.Identity(),

]

)

out_dim = default(out_dim, channels)

self.final_conv = nn.Sequential(

block_klass(dim, dim), nn.Conv2d(dim, out_dim, 1)

)

def forward(self, x, time):

x = self.init_conv(x)

t = self.time_mlp(time) if exists(self.time_mlp) else None

h = []

# downsample

for block1, block2, attn, downsample in self.downs:

x = block1(x, t)

x = block2(x, t)

x = attn(x)

h.append(x)

x = downsample(x)

# bottleneck

x = self.mid_block1(x, t)

x = self.mid_attn(x)

x = self.mid_block2(x, t)

# upsample

for block1, block2, attn, upsample in self.ups:

x = torch.cat((x, h.pop()), dim=1)

x = block1(x, t)

x = block2(x, t)

x = attn(x)

x = upsample(x)

return self.final_conv(x)

代码

文本

训练模型

代码

文本

定义训练参数，其中image_size即对应2D投影表示的空间分辨率

代码

文本

[15]

image_size = 32

channels = 1

batch_size = 128

代码

文本

导入数据，这里选择预先保存的凝聚多肽2D投影图

代码

文本

[16]

from torchvision import transforms

from torch.utils.data import DataLoader

from pathlib import Path

data_transforms = {

'train': Compose([

Resize(image_size),

CenterCrop(image_size),

ToTensor(),

Lambda(lambda t: (t * 2) - 1)])

}

from torchvision import datasets

data_dir = './DDPM/absorp_img/'

dataset = datasets.ImageFolder(data_dir, transform=data_transforms['train'])

dataloader = DataLoader(dataset, batch_size=batch_size, shuffle=True, drop_last=True)

results_folder = Path("./results/")

results_folder.mkdir(exist_ok = True)

save_and_sample_every = 1000

代码

文本

实例化U-net网络，对于小体量训练，我们只选取了3层编码/解码层

代码

文本

[17]

device = "cuda" if torch.cuda.is_available() else "cpu"

model = Unet(

dim=image_size,

channels=channels,

dim_mults=(1, 2, 4, )

)

model.to(device)

losses = []

代码

文本

如果需要，载入之前的训练权重

代码

文本

[18]

path_to_model = './DDPM/models_2Dimg/'

model.load_state_dict(torch.load(path_to_model + 'backup_1000_32x32x1' + '.pkl'))

<All keys matched successfully>

代码

文本

用pytorch的常用格式进行训练，其中学习率lr需要根据训练情况适当调节，这里简单的进行手动调节，分别在前期、中期和后期采用1e-3,1e-4,1e-5

代码

文本

[19]

from torch.optim import Adam

optimizer = Adam(model.parameters(), lr=1e-6)

"""Let's start training!"""

from torchvision.utils import save_image

epochs = 10

for epoch in range(epochs):

for step, batch in enumerate(dataloader):

optimizer.zero_grad()

batch = batch[0].to(device)

# Algorithm 1 line 3: sample t uniformally for every example in the batch

t = torch.randint(0, timesteps, (batch_size,), device=device).long()

loss = p_losses(model, batch[:, 0:channels, :,:], t, loss_type="huber")

if step % 100 == 0:

print("Loss:", loss.item())

losses.append(loss.item())

loss.backward()

optimizer.step()

Loss: 0.008132042363286018
Loss: 0.0077656847424805164
Loss: 0.011988483369350433

---------------------------------------------------------------------------
KeyboardInterrupt                         Traceback (most recent call last)
Cell In[19], line 10
      8 epochs = 10
      9 for epoch in range(epochs):
---> 10     for step, batch in enumerate(dataloader):
     11       optimizer.zero_grad()
     14       batch = batch[0].to(device)

File /opt/conda/lib/python3.8/site-packages/torch/utils/data/dataloader.py:634, in _BaseDataLoaderIter.__next__(self)
    631 if self._sampler_iter is None:
    632     # TODO(https://github.com/pytorch/pytorch/issues/76750)
    633     self._reset()  # type: ignore[call-arg]
--> 634 data = self._next_data()
    635 self._num_yielded += 1
    636 if self._dataset_kind == _DatasetKind.Iterable and \
    637         self._IterableDataset_len_called is not None and \
    638         self._num_yielded > self._IterableDataset_len_called:

File /opt/conda/lib/python3.8/site-packages/torch/utils/data/dataloader.py:678, in _SingleProcessDataLoaderIter._next_data(self)
    676 def _next_data(self):
    677     index = self._next_index()  # may raise StopIteration
--> 678     data = self._dataset_fetcher.fetch(index)  # may raise StopIteration
    679     if self._pin_memory:
    680         data = _utils.pin_memory.pin_memory(data, self._pin_memory_device)

File /opt/conda/lib/python3.8/site-packages/torch/utils/data/_utils/fetch.py:51, in _MapDatasetFetcher.fetch(self, possibly_batched_index)
     49         data = self.dataset.__getitems__(possibly_batched_index)
     50     else:
---> 51         data = [self.dataset[idx] for idx in possibly_batched_index]
     52 else:
     53     data = self.dataset[possibly_batched_index]

File /opt/conda/lib/python3.8/site-packages/torch/utils/data/_utils/fetch.py:51, in <listcomp>(.0)
     49         data = self.dataset.__getitems__(possibly_batched_index)
     50     else:
---> 51         data = [self.dataset[idx] for idx in possibly_batched_index]
     52 else:
     53     data = self.dataset[possibly_batched_index]

File /opt/conda/lib/python3.8/site-packages/torchvision/datasets/folder.py:231, in DatasetFolder.__getitem__(self, index)
    229 sample = self.loader(path)
    230 if self.transform is not None:
--> 231     sample = self.transform(sample)
    232 if self.target_transform is not None:
    233     target = self.target_transform(target)

File /opt/conda/lib/python3.8/site-packages/torchvision/transforms/transforms.py:95, in Compose.__call__(self, img)
     93 def __call__(self, img):
     94     for t in self.transforms:
---> 95         img = t(img)
     96     return img

File /opt/conda/lib/python3.8/site-packages/torch/nn/modules/module.py:1501, in Module._call_impl(self, *args, **kwargs)
   1496 # If we don't have any hooks, we want to skip the rest of the logic in
   1497 # this function, and just call forward.
   1498 if not (self._backward_hooks or self._backward_pre_hooks or self._forward_hooks or self._forward_pre_hooks
   1499         or _global_backward_pre_hooks or _global_backward_hooks
   1500         or _global_forward_hooks or _global_forward_pre_hooks):
-> 1501     return forward_call(*args, **kwargs)
   1502 # Do not call functions when jit is used
   1503 full_backward_hooks, non_full_backward_hooks = [], []

File /opt/conda/lib/python3.8/site-packages/torchvision/transforms/transforms.py:361, in Resize.forward(self, img)
    353 def forward(self, img):
    354     """
    355     Args:
    356         img (PIL Image or Tensor): Image to be scaled.
   (...)
    359         PIL Image or Tensor: Rescaled image.
    360     """
--> 361     return F.resize(img, self.size, self.interpolation, self.max_size, self.antialias)

File /opt/conda/lib/python3.8/site-packages/torchvision/transforms/functional.py:490, in resize(img, size, interpolation, max_size, antialias)
    488         warnings.warn("Anti-alias option is always applied for PIL Image input. Argument antialias is ignored.")
    489     pil_interpolation = pil_modes_mapping[interpolation]
--> 490     return F_pil.resize(img, size=output_size, interpolation=pil_interpolation)
    492 return F_t.resize(img, size=output_size, interpolation=interpolation.value, antialias=antialias)

File /opt/conda/lib/python3.8/site-packages/torchvision/transforms/_functional_pil.py:250, in resize(img, size, interpolation)
    247 if not (isinstance(size, list) and len(size) == 2):
    248     raise TypeError(f"Got inappropriate size arg: {size}")
--> 250 return img.resize(tuple(size[::-1]), interpolation)

File /opt/conda/lib/python3.8/site-packages/PIL/Image.py:2192, in Image.resize(self, size, resample, box, reducing_gap)
   2184             self = Image.reduce(self, factor, box=reduce_box)
   2185         box = (
   2186             (box[0] - reduce_box[0]) / factor_x,
   2187             (box[1] - reduce_box[1]) / factor_y,
   2188             (box[2] - reduce_box[0]) / factor_x,
   2189             (box[3] - reduce_box[1]) / factor_y,
   2190         )
-> 2192 return self._new(self.im.resize(size, resample, box))

KeyboardInterrupt:

代码

文本

查看Loss随着学习过程的变化。由于载入了之前训练过的模型，此时loss在很低的数值附近震荡、缓慢下降。

代码

文本

[ ]

try:

loss

except NameError:

pass

else:

plt.plot(losses)

plt.xlabel('Batch (100)')

plt.ylabel('Loss')

plt.show()

代码

文本

如有必要，存储训练模型的权重

代码

文本

[ ]

#torch.save(model.state_dict(), path_to_model + 'backup_1000_32x32x1.pkl')

代码

文本

采样与后处理

代码

文本

[ ]

num_sample = 6

samples = sample(model, image_size=image_size, batch_size=num_sample, channels=channels)

代码

文本

模型直接输出的结果需要经过2项后处理：

reshape: 将(batch_size, channels, height, width)转换为(batch_size, height, width, channels)方便图片显示
rescale: 由于一个格子中大部分区域都没有原子分布，因此2D投影表示中的众数对应着空无原子的区域。有鉴于此，我们将生成的图片中灰度小于众数的位置处的数值都取为众数，以人工消除散落的原子噪声.为了节约运行时间，只对最后5个时间步运行这个操作，通过调用plt.hist获得像素值的统计分布来确定众数.

代码

文本

[ ]

reshaped_imgs = [rearrange(x, 'b c h w -> b h w c') for x in samples]

from scipy import stats

def rescale(x):

for l in range(x.shape[0]):

#获取众数

hists = plt.hist(x[l,:,:,0].flatten(),bins=80)

plt.show()

plt.close()

mode=hists[1][np.argmax(hists[0])]

print(mode)

for i in range(x.shape[1]):

for j in range(x.shape[2]):

if x[l,i,j,0] < mode:

x[l,i,j,0] = mode

x[l,:,:,0] = (x[l,:,:,0]-np.min(x[l,:,:,0]))/(np.max(x[l,:,:,0])-np.min(x[l,:,:,0]))

return x

rescaled_imgs = []

for reshaped_img in reshaped_imgs[-5:-1]:

print(reshaped_img.shape)

rescaled_img = rescale(reshaped_img)

rescaled_imgs.append(rescaled_img)

代码

文本

查看生成数据的统计分布。第一张图original image是训练数据中某个batch的分布（数值已重新平移），可以看到最小值处分布有最多的像素点，这是因为大部分原子都凝聚在一起，投影表示图中大部分区域都没有原子，对应着像素值最小的点；第二张图是生成的一个batch在逆扩散初始时刻t=T的像素分布，可以看到其几乎就是高斯噪声；第三张图是该batch逆扩散至末态t=0的像素分布，此时已经和训练集分布有着接近的特征。

代码

文本

[ ]

fig,(ax1,ax2,ax3) = plt.subplots(3,1,num=2)

plt.subplots_adjust(hspace=0.5)

ax1.hist(batch.cpu().numpy()[-1][0].flatten(), bins=100)

ax1.set_title('original image')

ax2.hist(reshaped_imgs[0][0].flatten(), bins=100)

ax2.set_title('t=T')

ax3.hist(rescaled_imgs[-1][0].flatten(), bins=100)

ax3.set_title('t=0')

plt.show()

代码

文本

[ ]

imgs = rescaled_imgs

for i in range(imgs[-1].shape[0]):

if channels > 1:

fig,(ax1,ax2,ax3,ax4) = plt.subplots(1,4, figsize=(12,4), sharex=True)

ax1.imshow(imgs[-1][i,:,:,0])

ax1.set_title('x-coordinate')

ax2.imshow(imgs[-1][i,:,:,1])

ax2.set_title('y-coordinate')

ax3.imshow(imgs[-1][i,:,:,2])

ax3.set_title('z-coordinate')

ax4.imshow(imgs[-1][i,:,:,:])

ax4.set_title('all')

#plt.suptitle(title)

plt.show()

else:

plt.imshow(imgs[-1][i,:, :, 0])

plt.colorbar()

plt.show()

代码

文本

通过调用我们post在另一篇notebook“Gromacs分子动力学结构数据的2D表示”的函数接口，可以将生成的图片还原成伪3D的.gro文件并通过OVITO的软件可视化

代码

文本

[ ]

import process_gc as gc

path_to_results = './results_gro/'

imgs = [reshaped_imgs[0]] + rescaled_imgs

for ra in range(num_sample):

img_coord = rescaled_imgs[-1][ra]

gc.img_2Dcoords2gro([img_coord], resolution=image_size, file_name=str(ra)+'_test.gro', store_path=path_to_results)

gif_steps = np.linspace(0,timesteps-1, num=50)

for random_index in range(num_sample):

imgs_coord = []

for i in range(len(imgs)):

img_coord = imgs[int(i)][random_index]

imgs_coord.append(img_coord)

gc.img_2Dcoords2gro(imgs_coord, resolution=image_size, file_name=str(random_index)+'_diffusion.gro', store_path=path_to_results)

代码

文本

下图展示了生成结果的一个例子，包括从t=T步逆扩散至t=0步的伪3D结构和2D投影表示

代码

文本

最后我们可以存储模型权重以备之后调用

代码

文本

[ ]

#torch.save(model.state_dict(), path_to_model + 'backup' + '.pkl')

代码

文本

也可以生成逆扩散过程的gif动画，更形象的演示DDPM逆向解噪的过程。

代码

文本

[ ]

print(samples[0].shape)

print(np.max(samples[0]))

print(np.min(samples[0]))

import matplotlib.animation as animation

gif_steps = np.linspace(0,timesteps-1, num=20)

for random_index in range(num_sample):

fig = plt.figure()

ims = []

for i in range(len(imgs)):

im = plt.imshow(imgs[int(i)][random_index], animated=True)

ims.append([im])

animate = animation.ArtistAnimation(fig, ims, interval=200, blit=True, repeat=False)

animate.save(str(random_index)+'_diffusion.gif')

print('Saved!!')

代码

文本

总结与展望

代码

文本

我们将分子动力学优化好的凝聚多肽水溶液体系的结构数据，映射到图片格式的2D投影表示，送入DDPM进行训练、生成。
现阶段进行了没有元素分辨能力的单通道尝试，结果表明DDPM可以成功学习到凝聚多肽的形貌特征，并生成新的凝聚多肽结构的2D投影表示，及其还原的伪3D表示。
我们另外测试了2D投影表示+肽链序列共同学习的方案，和3D粗粒化网格方案，但没有取得好的效果。
下一步可以扩展对元素的分辨能力，并增加投影表示的分辨率

代码

文本

小组分工

代码

文本

为了确保比赛作品的完成度，我们小组采用同一套DDPM网络、两个投影表示方式并行推进的方式进行分工。胡家鸣负责难度相对较小的2D投影表示部分，结果已呈现于提交的notebook文档；杨珺婷负责风险更高的3D表示的尝试，因训练结果不佳，所以不再赘述。

代码

文本

Diffusion Model

已赞3

本文被以下合集收录

蛋白

bioinfo@sina.com

更新于 2024-09-02

9 篇1 人关注

graph

bohr589c3f

更新于 2024-04-18

8 篇0 人关注