

一. MD中用到的基本概念
为了更方便的进入分子动力学(Molecular Dynamics)这个领域,这里先介绍一些MD相关的基本概念。
1.1 势能面
势能面是分子内部原子或原子团相互作用的势能在核坐标配置空间中的映射,是量子化学和分子动力学研究中的基本概念。它描述了随着分子内部原子间距离和角度的变化,系统总势能的变化情况。这一面通常是多维的,每一维对应一个分子内部的坐标(例如键长、键角或二面角)。
势能面的局部最小值点代表分子的稳定构型(即基态和激发态的最小能量构型),而局部最大值点或鞍点通常对应于化学反应的过渡态,这些特殊点在反应路径上起关键作用。理解和计算势能面可以帮助预测和解释化学反应的动力学行为和机理,比如活化能的高低、反应速率以及反应途径的选择性。
势能面的计算和模拟通常依赖于量子化学方法,如波函数基础上的从头算(ab initio)方法和密度泛函理论(DFT),这些方法可以提供关于分子系统势能的详细信息。通过势能面,科学家能够设计更有效的化学反应和合成路径,以及更好地理解和预测分子行为。
1.2 MD积分算法
Verlet算法是一种在分子动力学模拟中常用的数值积分方法,用于计算粒子的运动。这种算法最初由物理学家Loup Verle提出,并且因其在物理上的稳定性和计算上的效率而广泛应用于模拟粒子系统的时间演化。
Verlet算法的基本思想是使用牛顿的第二定律,即力等于质量乘以加速度,来更新粒子的位置和速度。算法只需使用粒子的当前位置和前一个时间步的位置,以及当前力,就能计算出下一个时间步的位置。具体公式为: 其中, 是在时间 的粒子位置, 是作用在粒子上的力, 是粒子质量, 是时间步长。
Verlet算法的一个关键优点是它不直接计算粒子的速度,这可以避免因积分速度而产生的累积误差。此外,这种算法具有良好的能量守恒特性,特别适合于长时间的动力学模拟。然而,不计算速度也是其局限之一,因为在需要速度信息的情况下,必须通过位置数据间接计算,这可能导致额外的误差和计算成本。
Leapfrog算法是Verlet算法的一类变体,特别适用于分子动力学模拟中粒子的运动方程。它属于辛积分器(Symplectic integrator)的一种,这意味着它能够很好地保持能量和其他守恒量的长期稳定性,这对于长时间尺度的动力学模拟至关重要。
Leapfrog算法的命名来源于其计算步骤中的“跳跃”特性,即速度和位置的更新步骤是交错进行的。这种方法不仅提高了计算效率,而且减少了数值误差的累积。其基本公式包括:
速度的半步更新: 在这一步中,使用当前的力 (\mathbf{F}(t)) 更新速度的一半时间步。
位置的全步更新: 利用更新后的速度计算下一个时间点的位置。
速度的另一半步更新: 在新的位置上计算力,然后完成速度的更新。
Leapfrog算法的优势在于其简单性和效率,特别是在处理大型系统时,这些特性尤为重要。由于速度和位置的更新是分离的,这使得算法能有效处理那些力与位置强烈耦合的动力学系统。此外,由于其辛性质,Leapfrog算法在模拟过程中能较好地保持系统的总能量不变,这对于保证物理模拟的准确性至关重要。
在实际应用中,Leapfrog算法广泛用于天体物理学、化学动力学和其他需要精确模拟粒子动态的领域。其高效的计算性能和较低的误差积累使得它成为一个非常受欢迎的选择。
1.3 系综
在统计力学中,系综是一种理想化的物理系统集合,用于描述热力学性质。不同的系综根据其守恒的物理量(如能量、体积、粒子数)和控制的参数(如温度、压力)来定义。常见的系综包括微正则系综(NVE)、正则系综(NVT)和等温等压系综(NPT)等。这些系综在分子动力学模拟软件LAMMPS中得到了广泛的实现和应用。
NVE系综是一个封闭系统,其中粒子数(N)、体积(V)和能量(E)都保持不变。在NVE系综中,没有与外部环境的能量或物质交换。这种系综在模拟能量守恒系统,如孤立系统中非常有用。在LAMMPS中,NVE系综可以通过fix nve命令来实现,这个命令使用经典的牛顿力学来积分系统的运动方程,不对温度或压力进行调控。
NVT系综中,粒子数(N)、体积(V)和温度(T)是固定的。在这种系综中,系统可以与一个温度恒定的热库进行能量交换,但不能交换粒子或改变体积。这种系综适用于研究温度效应对物质性质的影响。在LAMMPS中,NVT系综通常通过fix nvt命令实现,该命令使用诸如Nosé-Hoover热浴等热力学统计方法来控制系统温度。
NPT系综中,粒子数(N)、压力(P)和温度(T)都是固定的。这种系综允许系统的体积随着模拟的进行自由变化以维持恒定的压力,同时也与一个温度恒定的热库进行能量交换。这是研究物质在实际应用中如何响应环境压力变化的重要模型。在LAMMPS中,NPT系综可以通过fix npt命令实现,该命令同时控制温度和压力,使系统保持在预设的温度和压力下运行。
在μVT(巨正则系综)系综中,化学势(μ)、体积(V)和温度(T)保持恒定,而粒子数可以变化。这种系综适用于研究相变和吸附等现象。在LAMMPS中,可以使用fix gcmc即巨正则蒙特卡洛命令来实现μVT系综,这个命令允许在模拟过程中插入和删除粒子,以模拟在给定的化学势下的粒子数波动。
在LAMMPS中,这些系综的实现通常依赖于fix命令,该命令定义了如何对系统中的粒子进行积分。
二. DPMD实战
这里考虑一个Ti-Mo合金的系统的分子动力学模拟,使用的DP model为来自AiS square的TiMo model。
LAMMPS的输入包括TiMo.data, TiMo.in文件,其中*.data包含的是初态的原子位置构型,部分代码如下:
而TiMo.in则保存了LAMMPS模拟的设置,包含如下部分:
其中包括了单位设置(时间单位对金属而言设置为ps)、边界设置(周期性)、原子构型、相互作用建模(采用DeePMD模型)、初态速度设置、NPT系综模拟设置、RDF(径向分布函数)计算、MSD(均方位移分布函数)计算、导出设置。
运行
即可开始DPMD模拟,模拟过程需要几分钟。模拟结束后将产生timo.dump, timo.msd, timo.rdf文件。其中timo.dump存储每个模拟步长后的原子位置,timo.msd和timo.rdf分别存储用于计算MSD和RDF的数据,我们需要用到这些数据来计算。
这里给出了计算RDF的python代码:
以及计算MSD的python代码:
运行后即可得到RDF和MSD的直观结果。这里考虑了不同温度下的RDF和MSD,分别为5K,2000K,5000K,7000K:
RDF图像:
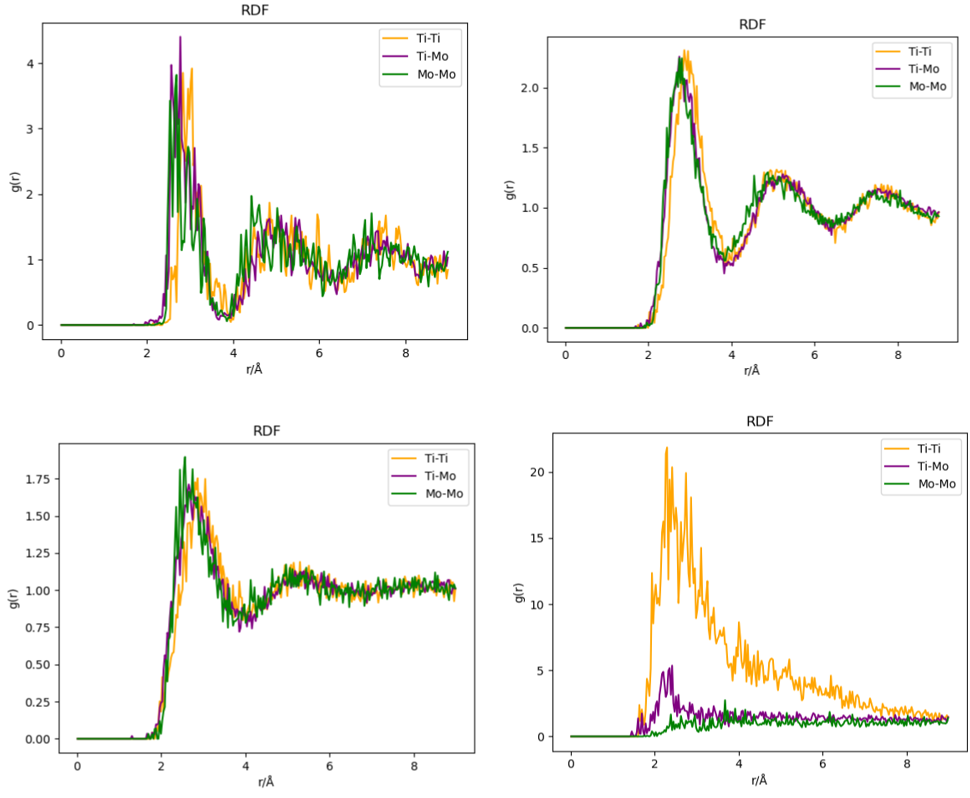
MSD图像:






