

致谢:
原notebook链接:https://bohrium.dp.tech/notebooks/69751647598/update
一、元素背景知识
1.镁
(1)发现过程
镁元素最早是由英国化学家约瑟夫·布莱克(Joseph Black)在1755年发现的.他首次从石灰石中分离出了镁氧化物,但当时并未意识到这是一种新的元素.直到1808年,英国化学家汉弗莱·戴维(Humphry Davy)通过电解镁氧化物,成功分离出了纯净的镁金属.这一发现确认了镁是一种新的元素.1828年法国科学家安东尼·比西用金属钾还原熔融的无水氯化镁得到纯镁.
(2)物理化学性质
物理性质
热学性质 常温下镁为固态,呈现出银白色的典型金属外观.其熔点为650 ℃,沸点为1091 ℃.
熔化热 8.48 kJ·mol^(-1)
汽化热 128 kJ·mol^(-1)
比热容 24.869 J·mol^(-1)·K^(-1)
热导率 156 W·m^(-1)·K^(-1)
膨胀系数 (25 °C) 24.8 µm·m^(-1)·K^(-1)
力学性质
室温下,镁的密度为1.738 g·cm^(-3). 在熔点650 ℃时液态镁的密度为1.584 g·cm^(-3)
声速 4940 m·s^(-1)
杨氏模量 45 GPa
剪切模量 17 GPa
体积模量 45 GPa
莫氏硬度 2.5
布氏硬度 260 MPa
化学性质
与空气反应
镁的化学性质十分活泼,需要保存在真空或稀有气体中.暴露在空气中会迅速氧化.
2Mg(s)+O_2 (g)=2MgO(s)
这层氧化层具有保护作用,可以阻止内部的镁被进一步氧化.如果加热至高温,镁可以在空气中稳定的燃烧.
与水反应
Mg(s)+2H_2 O(l)=Mg(OH)_2 (s)+H_2 (g)
该反应在室温下即可进行,但速率很慢,生成的氢气气泡难以察觉.加热后速率显著变快.
与酸反应
Mg(s)+2HCl(aq)=MgCl_2 (aq)+H_2 (g)
该反应速率很快,剧烈放热,产生大量氢气气泡.
Mg(s)+H_2 SO_3 (aq)=MgSO_3 (s)+H_2 (g)
该反应初始时速率很快,随后由于生称的亚硫酸镁难溶于水,速率会逐渐减慢,在反应物消耗完之前就会停止.
还原性
镁可以被卤素氧化,即使是最不最不活泼的碘也可以在常温下与镁发生化合
Mg(s)+I_2 (s)=MgI_2 (s)
在高温环境下,通常被认为不支持燃烧的氮气可以与镁反应,并稳定燃烧.
3Mg(s)+N_2 (g)=Mg_3 N_2 (s)
通常同样被认为不支持燃烧的二氧化碳也可以与镁反应,并稳定燃烧.因此镁金属引起的火灾不能使用二氧化碳灭火器.
2Mg(s)+CO_2 (g)=2MgO(s)+C(s)
(3)常见化合物
主要矿石
菱镁矿 MgCO_3,硼镁矿 Mg_2 B_2 O_4 (OH). 硝酸镁 Mg(NO_3 )_2,用于在浓硝酸生产中作为脱水剂. 高氯酸镁 Mg(ClO_4 )_2,实验室常用的脱水剂,可反复使用. 叶绿素 叶绿素a,C_55 H_72 O_5 N_4 Mg 叶绿素b,C_55 H_70 O_6 N_4 Mg
镁粉:常用于举重、单双杠等体育项目中的白色粉末,起防滑作用.主要成分为碳酸镁MgCO_3.
(4)潜在用途
轻合金材料:由于镁的密度仅有1.738 g·cm^(-3),显著低于绝大多数其它金属,因此镁合金可以应用于航空航天、汽车制造、自行车等领域,用于制造轻量化的结构件、外壳、零部件等.未来更高性能和镁合金有希望改进战斗机、船舶的性能,更低成本的镁合金也有希望用于手机、电脑等民用产品上,减轻重量.
2、镱
(1)发现过程
1878年,瑞士化学家让-夏尔·加利萨·德马里尼亚从一种称为“Erbia”的稀土物质中分离出新的成分,并以矿物的发现地瑞典伊特比村将该成分命名为“Ytterbia”.他猜测Ytterbia是某新元素的化合物,因此又把该元素命名为“Ytterbium”,即镱元素.1907年,乔治·于尔班、卡尔·奥尔·冯·威尔士巴赫和查尔斯·詹姆士分别从德马里尼亚的镱样本中提取出了又一新元素,即镥.经过不少的讨论之后,科学界决定保留原名镱,并舍弃了威尔士巴赫所建议的“Aldebaranium”.1953年,科学家才制得纯度较高的镱金属样本.
(2)物理化学性质
镱金属质软、可延展,在纯态时有明亮的银色金属光泽.镱金属拥有三种同素异形体,分别以希腊字母α、β和γ表示.室温下镱处于β型,具有面心立方晶体结构;高温下的γ型具有体心立方结构;低温下稳定的α型则具有六方晶系结构.β型的电导率与其他金属相近,但在16000个大气压(1.6 GPa)下会呈现半导体性质.其电阻率在加压至39,000个大气压(3.9 GPa)时会增加十倍,但到40,000大气压(4.0 GPa)时却会将至室温电阻率的10%左右. 和低温下呈反铁磁性和/或铁磁性的其他稀土金属不同,镱在1.0 K以上具有顺磁性.α型则有抗磁性.
热学性质
常温下镱为固态.其熔点为824 ℃,沸点为1196 ℃.
熔化热 7.66 kJ·mol^(-1)
汽化热 129 kJ·mol^(-1)
比热容 26.74 J·mol^(-1)·K^(-1)
热导率 38.5 W·m^(-1)·K^(-1)
膨胀系数 (25 °C) 26.3 µm·m^(-1)·K^(-1)
力学性质
室温下,镱的密度为6.90 g·cm^(-3). 在熔点824 ℃时液态镱的密度为6.21 g·cm^(-3)
声速 1950 m·s^(-1)
杨氏模量 23.9 GPa
剪切模量 9.9 GPa
体积模量 30.5 GPa
布氏硬度 343 MPa
维氏硬度 206 MPa
化学性质
化合价
镱一般呈三价氧化态,但它亦可以形成二价化合物.这种特性在几乎只形成三价化合物的镧系元素中较为罕见.黄绿色的镱(II)离子是一种强还原剂,会在水中被水氧化,所以只有无色的镱(III)离子才能稳定地出现在水溶液中.
与水反应
2Yb(s)+6H_2 O(l)=2Yb(OH)_3 (aq)+3H_2 (g)
该反应在室温下即可进行,但速率很慢,加热后速率显著变快.
与酸反应
在镱与盐酸的反应中,首先会生成黄色的二氯化镱
Yb(s)+2HCl(aq)=YbCl_2 (aq)+H_2 (g)
Yb^(2+)离子具有很强的还原性,短时间之内就会被H^+进一步氧化成无色的Yb^(3+)离子
2YbCl_2 (aq)+2HCl(aq)=2YbCl_3 (aq)+H_2 (g)
因此,溶液会先呈现黄色,短时间后会由黄色变为无色.
(3)常见化合物
卤化物
镱可以和氟、氯、溴及碘形成二卤化物和三卤化物.二卤化物在常温下会受卤素的氧化,在高温下则会歧化形成三卤化物和镱金属.
镱的一些卤化物被用作有机合成反应的试剂.例如,三氯化镱YbCl_3是一种路易斯酸,也是羟醛反应和狄尔斯–阿尔德反应的催化剂.二碘化镱YbI_2和二碘化钐一样可以用作偶联反应的还原剂.三氟化镱YbF_3是一种惰性无毒的牙齿填充材料.它还是一种优良的X光造影剂.
(4)潜在用途
光学应用
三价镱离子可以做激光活性媒质的掺杂剂,特别用于固态激光器和双包层光纤激光器中.镱激光器效率高,寿命长,且能够产生很短的脉冲.
催化剂
镱化合物可以在有机反应中作为催化剂.
二、DFT算法
密度泛函理论(DFT)是一种计算量子力学建模方法,用于物理学、化学和材料科学领域,用于研究多体系统的电子结构(或核结构)(主要是基态),特别是原子、分子和凝聚相。利用这一理论,可以通过使用泛函(即另一个函数的函数)来确定多电子系统的性质。在DFT的情况下,这些是空间相关电子密度的泛函。DFT是凝聚态物理学、计算物理学和计算化学中最流行和多功能的方法之一。
自上世纪70年代以来,DFT在固态物理学计算中非常受欢迎。然而,直到1990年代,DFT在量子化学计算中的精度还不够,当时理论中使用的近似值得到了很大改进,以更好地模拟交换和相关相互作用。与只考虑交换的哈特里-福克理论及其包含电子相关性的后代相比,计算成本相对较低。因此,DFT已成为核谱学方法的重要工具,例如莫斯堡尔谱学或扰动角相关,以便理解晶体中特定电场梯度的来源。
尽管最近有所改进,但使用密度泛函理论正确描述分子间相互作用(对于理解化学反应至关重要),特别是范德华力(色散);电荷转移激发;过渡态,全局势能面,杂质相互作用和一些强相关系统;以及在半导体中计算带隙和铁磁性方面仍然存在困难。对色散的不完整处理可能会影响DFT的准确性(至少在单独使用且未校正时),在处理由色散主导的系统(例如相互作用的惰性气体原子)或色散与其他效应显著竞争的情况下(例如在生物分子中)可能会受到影响。新的DFT方法的发展旨在克服这一问题,通过对泛函进行改变或包含添加项。经过调整参数获得的DFT势不再是真正的DFT势,因为它们不是关于电荷密度的交换相关能量的泛函导数。因此,在这种情况下,第二定理是否成立尚不清楚。
在计算材料科学的背景下,从头算DFT计算允许基于量子机械考虑对材料行为进行预测和计算,而不需要更高阶参数,如基本材料性质。在当代DFT技术中,电子结构是通过作用于系统电子的势来评估的。这种DFT势被构建为外部势Vext和有效势Veff的总和,前者仅由系统的结构和元素组成确定,后者代表电子间相互作用。因此,可以将具有n个电子的材料代表性超晶胞的问题研究为n个一电子薛定谔式方程组,也被称为Kohn-Sham方程。
在密度泛函理论(DFT)当中,原子核被视为固定的,生成一个静态外部势能V,电子在其中运动。一个稳态的电子状态由满足多电子定态薛定谔方程的波函数Ψ(r1,…,rN)描述。DFT的关键变量是电子密度n(r),它是波函数Ψ的归一化形式。DFT将复杂的多体问题映射到一个没有电子-电子相互作用的单体问题上。通过最小化能量泛函,可以得到基态密度n0,从而获得所有其他基态可观测量。为了解决这个变分问题,可以应用未定乘子的拉格朗日方法。首先,考虑一个不显式包含电子-电子相互作用能项的能量泛函,然后基于这个辅助的非相互作用系统的能量,可以推导出Kohn-Sham方程,从而得到能够复制原多体系统密度的轨道。通过求解辅助非相互作用系统的Kohn-Sham方程,可以获得重现原始多体系统密度n(r)的轨道φi。这些轨道是通过重复迭代计算的方式获得的。最终,DFT提供了一种更加灵活的方法来解决多体薛定谔方程,尤其适用于大型和复杂系统。
(2)STRU文件
(3)KPT文件
(4)INPUT文件
(5)收敛性测试
将以上所有文件放在同一个文件夹里,输入
改变INPUT文件中ecutwfc的值,扫描ecut参数.得到的结果为

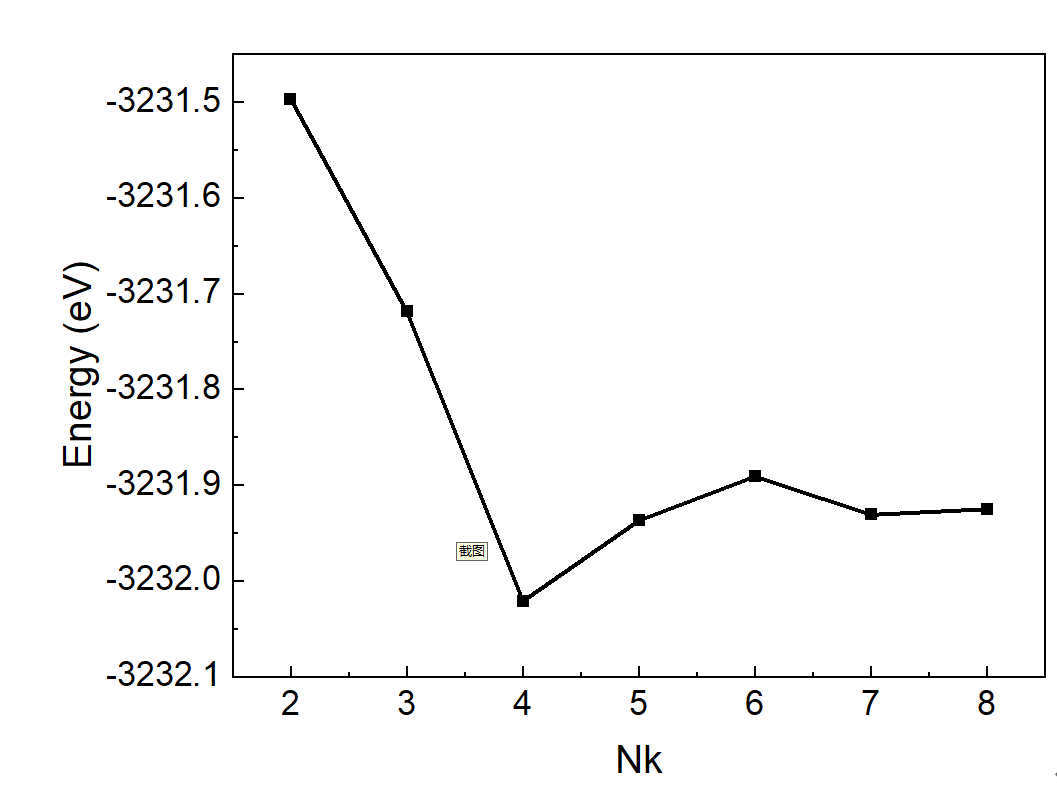
改变KPT文件中的K points个数.
系统总能量
计算时间

2.镱
(2)STRU文件
(3)KPT文件
(4)INPUT文件
将以上所有文件放在同一个文件夹里,输入
四、ABACUS软件计算晶格结构
1.镁
(1)STRU文件
(2)KPT文件
(3)INPUT文件
(4)计算
以上所有文件放在同一个文件夹里,输入
在结果文件夹OUT.Mg中,包含最终优化结构的文件STRU_NOW.cif

2.镱
(1)STRU文件
(2)KPT文件
(3)INPUT文件
(4)计算
在结果文件夹OUT.Yb中,包含最终优化结构的文件STRU_NOW.cif

3.氧化镁
(1)STRU文件
(2)KPT文件
(3) INPUT文件
(4)计算
在结果文件夹OUT.MgO中,包含最终优化结构的文件STRU_NOW.cif

4.氧化镱
(1)STRU文件
(2)KPT文件
(3)INPUT文件
(4)计算
在结果文件夹OUT.YbCl3中,包含最终优化结构的文件STRU_NOW.cif








